Ряд динамики (временной ряд, time series) – это последовательность изменяющихся во времени значений показателя, расположенных в хронологическом порядке.

Составными элементами ряда динамики являются: значения показателя – уровни ряда и периоды (годы, кварталы, месяцы, сутки) или моменты (даты) времени. Уровни ряда обычно обозначаются через y, моменты или периоды времени, к которым относятся уровни, – через t.

Ряды динамики, как правило, представляют в виде таблицы и/или диаграммы динамики. Классификация рядов динамики представлена на рис. 36.


 

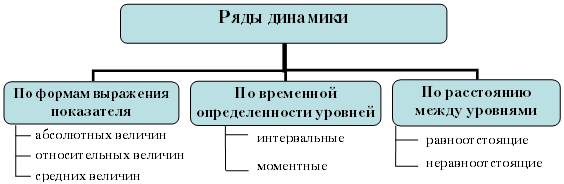
Рис. 36. Классификация рядов динамики
Ряд динамики абсолютных величин представлен в первой строке таблицы 55, ряд средних величин – в 3-й строке; ряд относительных величин – во 2-й строке.
Таблица 55.

 

Число построенных квартир и их средний размер в РФ

	2008	2009	2010	2011	2012
Число квартир, тыс.	768	702	717	786	838
Число однокомнатных квартир, % от общего количества	33	33	34	36	38
Средний размер квартир, м2 общей площади	83,4	85,3	81,5	79,3	78,4

Уровни моментных рядов динамики характеризуют явление по состоянию на определенный момент времени (табл. 56).
Таблица 56.
Численность персонала фирмы в I полугодии 2013 г.

(на 1-е число месяца)

Дата	1.01	1.02	1.03	1.04	1.05	1.06
Численность персонала, чел.	780	810	880	930	940	970

 

Уровни моментных рядов абсолютных величин нельзя суммировать, так как в них повторяются одни и те же единицы совокупности.

---

Ряд, в котором уровни характеризуют результат, накопленный или вновь произведенный за определенный интервал времени, называется интервальным рядом (табл. 57).
Таблица 57.
Динамика объема розничного товарооборота в регионе

 

Месяц	Январь	Февраль	Март	Апрель	Май	Июнь
Товарооборот, млн руб.	3,4	3,2	3,6	3,8	3,5	3,7

 

В отличие от моментных рядов, сумма уровней интервального ряда является реальным показателем, например, общий объем розничного товарооборота за I полугодие (с января по июнь).

Ряды динамики следующих друг за другом периодов или повторяющихся через равные промежутки дат называются равноотстоящими. Если же в рядах даются прерывающиеся периоды или неравномерные промежутки между датами, то ряды называются неравноотстоящими.
Важнейшим условием правильного построения рядов динамики является сопоставимость входящих в него уровней, под которой понимается соответствие всех уровней ряда динамики:

·     единым единицам измерения и единицам счета;

·     единой методологии учета и расчета показателей;

·     единым административным и территориальным границам.
Чтобы привести уровни ряда динамики к сопоставимому виду, используют прием, который носит название смыкание рядов динамики. Под смыканием понимают объединение в один ряд (более длинный) двух или нескольких рядов динамики с несопоставимыми уровнями. Для смыкания необходимо, чтобы для одного из периодов (переходного) имелись данные, исчисленные по разной методологии (или в разных границах). По такому уровню рассчитывают соотношение значений показателя – коэффициент пересчета и все остальные уровни умножаются на значение коэффициента. Другой способ смыкания рядов заключается в том, что уровни года, в котором произошли изменения принимаются за 100 %, а остальные пересчитываются в процентах по отношению к этим уровням соответственно.

При сравнительном анализе развития во времени экономических показателей стран, административных и территориальных районов ряды динамики приводятся к одному основанию – к одному периоду или моменту времени

---

, уровень которого принимается за базу сравнения, а все остальные уровни выражаются в виде коэффициентов или в процентах по отношению к нему.
Вопрос 2. Аналитические показатели динамики.
Для количественной оценки развития явлений во времени используются аналитические показатели динамики. Они характеризуют в абсолютном или относительном выражении как изменилось значение показателя в одном уровне рассматриваемого ряда динамики по сравнению с другим уровнем. При этом сравниваемый уровень называют текущим, или отчетным, а уровень, с которым происходит сравнение – базисным.

Поскольку время развивается всегда однонаправлено, каждый уровень ряда динамики можно сравнить с предшествующим или с другим, более ранним уровнем, выбранным за базу сравнения (как правило, первым в ряду). В первом случае рассчитанные аналитические показатели называют цепными, а при сравнении всех уровней ряда с фиксированным уровнем – базисными (рис. 37).

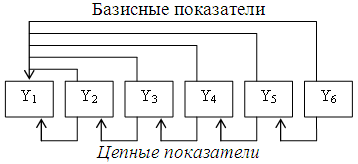
Рис. 37. Построение цепных и базисных аналитических показателей динамики
К основным аналитическим индивидуальным показателям динамики относятся: абсолютный прирост, темп роста и прироста, абсолютное значение одного процента прироста (табл. 58).
Таблица 58.

 

Индивидуальные аналитические показатели динамики

Название и обозначение показателя	Содержание показателя	Формула расчета
		Цепные показатели	Базисные показатели
Абсолютный прирост	Показывает, на сколько единиц измерения выросло или сократилось значение уровня в текущем периоде по сравнению с предшествующим или выбранным за базу сравнения.
Темп роста Тр	В долях единицы (коэффициентах). Показывает, во сколько раз данный уровень ряда больше предшествующего или базисного уровня. В процентах. Показывает, сколько процентов составляет величина уровня в текущем периоде от его величины в предшествующем или выбранном за базу сравнения периоде.
Темп прироста Тпр	Показывает, на сколько процентов изменился сравниваемый уровень по отношению к предшествующему уровню или принятому за базу сравнения.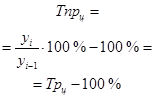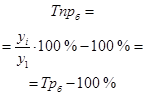
Абсолютное значение одного процента прироста |%|	Показывает сколько абсолютных единиц приходится на 1 % прироста значения уровня в текущем периоде по сравнению с предшествующим.		-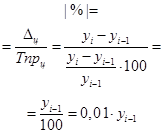
Обозначения: yi – рассматриваемый уровень ряда динамики – текущий уровень; yi–1 – уровень ряда, предшествующий текущему; y1 – начальный уровень ряда динамики (или принятый за базу сравнения).

---

Для обобщения данных об изменении уровней ряда динамики рассчитываются средние аналитические показатели динамики, к которым относятся: средний уровень ряда; средний абсолютный прирост; средний темп роста; средний темп прироста.

Формулы для расчета среднего уровня ряда приведены в табл. 59. Примеры расчета среднего уровня в моментных рядах динамики рассмотрены в теме 5 (вопрос 4, Средняя хронологическая).
Таблица 59.

 

Расчет среднего уровня ряда динамики

 

Название и обозначение показателя	Содержание показателя	Формула расчета
		Для рядов с равноотстоящими уровнями	Для рядов с неравноотстоящими уровнями
Средний уровень ряда	Характеризует средний размер уровня в каждый период или момент времени в течение рассмотренного временного интервала	Для интервальных рядов динамики
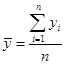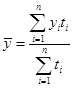		Для моментных рядов динамики
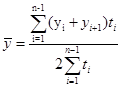Обозначения: yi – значения уровней рассматриваемого ряда динамки; n – число уровней ряда; y1 – начальный уровень ряда динамики; ti– продолжительность интервалов времени между уровнями; (число периодов времени, в которых значение уровня не изменялось).

Расчет остальных средних аналитических показателей осуществляется по формулам таблицы 60.
Таблица 60.

 

---

Средние аналитические показатели динамики

Название и обозначение показателя	Содержание показателя	Формула расчета
Средний абсолютный прирост	Показывает, на сколько единиц измерения в среднем вырастало или сокращалось значение показателя от уровня к уровню в течение рассмотренного периода динамики.
Средний темп роста	В долях единицы (коэффициентах). Показывает, во сколько раз в среднем возрастало или сокращалось значение показателя от уровня к уровню в течение рассмотренного периода динамики.   В процентах. Показывает, сколько в среднем процентов последующий уровень составляет от предыдущего в течение всего периода динамики.	Для рядов с равноотстоящими уровнями 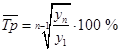      Для рядов с неравноотстоящими уровнями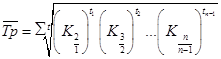
Средний темп прироста	Показывает, на сколько процентов в среднем возрастала или сокращалась величина показателя от уровня к уровню в течение рассмотренного периода динамики.
Обозначения: yi – рассматриваемый уровень ряда динамики – текущий уровень; yi–1 – уровень ряда, предшествующий текущему; y1 – начальный уровень ряда динамики; ti – продолжительность интервалов времени между уровнями; (число периодов времени, в которых значение уровня не изменялось); К – соответствующий коэффициент роста – темп роста, выраженный в долях единицы.

---

Смотрите также файлы

• Классный частренинг Мотивация учения.pdf

• 2. Письменно ответьте на вопросы Понятие об антропогенном кризисе и катастрофе.doc

• Решение Определим фондоотдачу (фотд) Фотд 42000 16000 2,625 тыс руб.docx

• Методические указания по выполнению лабораторной работы по дисциплине Теплофизика для студентов направления 20. 03. 01 Техносферная безопасность.pdf

• Фгбоу во ниу мэи.docx