ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 03.05.2024
Просмотров: 180
Скачиваний: 0
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Средний абсолютный прирост является обобщающим показателем абсолютной скорости изменения явления во времени, а средний темп роста оценивает среднюю интенсивность изменения уровней ряда динамики.
Пример 1. По данным об объеме экспорта РФ со странами дальнего зарубежья за 2007–2011 гг. рассчитаем аналитические показатели ряда динамики (табл. 61.).
1. Рассчитаем цепные (гр. 2 табл. 61) и базисные (гр. 3 табл. 61) абсолютные приросты:
Цепные (по сравнению с предшествующим годом):
Таблица 61.
Объем экспорта РФ со странами дальнего зарубежья в 2007–2011 гг. (млрд долл. США)
| Год | Объем экспорта, млрд долл. США | Абсолютный прирост, млрд долл. США | Темп роста, % | Темп прироста, % | Абсолютное значение 1 % прироста, млрд долл. США | |||
| по сравн. с предш. годом | по сравн. с 2007 г. | по сравн. с предш. годом | по сравн. с 2007 г. | по сравн. с предш. годом | по сравн. с 2007 г. | |||
| | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 2007 | 300,0 | - | - | - | - | - | - | - |
| 2008 | 400,0 | 100,0 | 100,0 | 133,33 | 133,33 | 33,33 | 33,33 | 3,000 |
| 2009 | 255,0 | -145,0 | -45,0 | 63,75 | 85,00 | -36,25 | -15,00 | 4,000 |
| 2010 | 338,0 | 83,0 | 38,0 | 132,55 | 112,67 | 32,55 | 12,67 | 2,550 |
| 2011 | 438,0 | 100,0 | 138,0 | 129,59 | 146,00 | 29,59 | 46,00 | 3,380 |
| Итого | 1731,0 | 138,0 | - | - | - | - | - | - |
Базисные (по сравнению с 2007 г.):
2. Рассчитаем цепные (гр. 4) и базисные (гр. 5) темпы роста:
Цепные (по сравнению с предшествующим годом):
Базисные (по сравнению с 2007 годом):
3. Рассчитаем цепные (гр. 6) и базисные (гр. 7) темпы прироста:
Цепные (по сравнению с предшествующим годом):
Тпр08/07 = 133,33 % – 100 % = 33,33 %
Тпр09/08 =63,75 % – 100 % = -36,25 %
Тпр 10/09 =132,55 % – 100 % = 32,55 %
Тпр 11/10 =129,59 % – 100 % = 29,59 %
Базисные (по сравнению с 2007 годом):
Тпр 08/07 = 133,33 % – 100 % = 33,33 %
Тпр 09/07 =85,00 % – 100 % = -15,00 %
Тпр 10/07 =112,67 % – 100 % = 12,67 %
Тпр 11/07 =146,00 % – 100 % = 46,00 %
4. Рассчитаем абсолютное значение одного процента прироста (гр. 8):
|%|2008 = у2007 * 0,01 =300,0 * 0,01 = 3,000 млрд долл. США
|%|2009 = у 2008 * 0,01 =400,0 * 0,01 = 4,000 млрд долл. США
|%|2010 = у 2009 * 0,01 =255,0 * 0,01 = 2,550 млрд долл. США
|%|2011 = у 2010 * 0,01 =338,0 * 0,01 = 3,380 млрд долл. США
5. Рассчитаем среднегодовой объем экспорта РФ в страны дальнего зарубежья за 2007–2011 гг. Рассматриваемый ряд динамики является интервальным рядом с равноотстоящими уровнями, поэтому используем формулу средней арифметической простой:
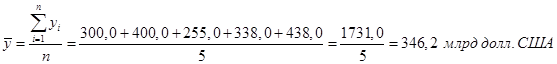
т.е. в среднем в период с 2007 по 2011 г. РФ ежегодно экспортировала в страны дальнего зарубежья товаров на сумму 346,2 млрд руб.
6. Определим средний абсолютный прирост объема экспорта РФ в страны дальнего зарубежья в 2007–2011 гг. Он составит:
Это означает, что в среднем за 2007–2011 гг. объем экспорта РФ в страны дальнего зарубежья ежегодно возрастал на 34,5 млрд долл. США.
7. Рассчитаем средний темп роста объема экспорта РФ в страны дальнего зарубежья в 2007–2011 гг.
Таким образом, в среднем объем экспорта РФ в страны дальнего зарубежья в период с 2007 по 2011 г. ежегодно возрастал в 1,0992 раза.
8. Найдем значение среднего темпа прироста. Поскольку средний темп роста объема экспорта РФ в страны дальнего зарубежья в 2007–2011 гг. составил 109,92 %, отсюда средний темп прироста будет равен:
Соответственно, в течение 2007–20011 гг. объем экспорта РФ в страны дальнего зарубежья в среднем ежегодно возрастал на 9,92 %.
Вопрос 3. Тенденция ряда динамики и методы ее выявления.
Под основной тенденцией развития ряда динамики понимают изменение, определяющее общее направление развития. Для выявления основной тенденции развития в статистике применяются две группы методов (рис. 38):

Рис. 38. Методы выявления тенденции в рядах динамики
Аналитическое выравнивание основано на расчете теоретических значений уровня ряда по наиболее подходящей модели их изменения. Модель представляет собой уравнение функции, позволяющей получить значения уровней ряда на основании значений фактора времени y = f(t). График теоретических значений образует линию, проведенную между конкретными уровнями ряда таким образом, чтобы она отражала тенденцию, присущую ряду, и одновременно освободила его от незначительных колебаний.
Механическое выравнивание (сглаживание) уровней ряда динамики осуществляется с использованием фактических значений соседних уровней. В результате получается новый ряд динамики, в котором колебания уровней в значительной мере погашены и основная тенденция развития этого ряда проступает более наглядно.
Метод укрупнения интервалов основан на укрупнении периодов времени, к которым относятся уровни. Например, ряд недельных данных можно преобразовать в ряд помесячной динамики, ряд квартальных данных заменить годовыми уровнями. Уровни нового ряда могут быть получены путем суммирования уровней исходного ряда либо могут представлять средние значения, рассчитанные по соответствующим уровням.
Метод скользящей средней. Выравнивание или сглаживание ряда динамики методом скользящих средних сводится к замене фактических уровней ряда расчетными уровнями, которые в меньшей степени подвержены колебаниям, что способствует более четкому проявлению тенденции развития. Сглаживание ряда динамики с помощью скользящей средней заключается в том, что вычисляется средний уровень из определенного числа первых по порядку уровней ряда, затем средний уровень из такого же числа уровней начиная со второго, далее – начиная с третьего и т.д. Таким образом, при расчете средних уровней они как бы «скользят» по ряду динамики от его начала к концу, каждый раз отбрасывая один уровень вначале и добавляя один следующий. Отсюда название – скользящая средняя.
Каждое звено скользящей средней – это средний уровень за соответствующий период, который относится к середине выбранного периода, если число уровней ряда динамики нечетное.
Нахождение скользящей средней по четному числу уровней ряда динамики несколько сложнее, так как средняя может быть отнесена только к середине между двумя датами, находящимся в середине интервала сглаживания. Например, средняя, найденная для четырех первых уровней, относится к середине между вторым и третьим уровнями, средняя из значений показателя, стоящих в ряду динамики на втором, третьем, четвертом и пятом местах, придется на середину между третьим и четвертым уровнями, и так далее. Чтобы ликвидировать такой сдвиг, применяют способ центрирования.
Центрирование заключается в нахождении средней из двух смежных скользящих средних для отнесения полученного уровня к определенной дате. Для этого необходимо найти скользящие суммы, затем по этим суммам рассчитать скользящие средние нецентрированные и после этого произвести центрирование – последовательно найти средние арифметические значения из соседних нецентрированных скользящих средних.
Пример 2. Покажем расчет скользящих средних за 3 и 4 месяца по данным, представленным в таблице 62.
Таблица 62.
Объем оказанных платных услуг населению региона за 2012 г.
| Месяц | Объем оказан- ных услуг, млн руб. | Трехуровневые скользящие суммы | Трехуровневые скользящие средние | Четырехуров-невые скользящие суммы | Четырехуровневые скользящие средние нецентри- рованные | Четырехуровневые скользящие средние центриро- ванные |
| А | 1 | 2 | 3 | 4 | 5 | 6 |
| январь | 13,3 | - | - | - | | - |
| февраль | 13,4 | - | 13,40 | - | | - |
| март | 13,5 | 40,2 | 13,43 | - | | 13,44 |
| апрель | 13,4 | 40,3 | 13,50 | 53,6 | 13,40 | 13,53 |
| май | 13,6 | 40,5 | 13,60 | 53,9 | 13,48 | 13,64 |
| июнь | 13,8 | 40,8 | 13,80 | 54,3 | 13,58 | 13,80 |
| июль | 14,0 | 41,4 | 14,00 | 54,8 | 13,70 | 13,96 |
| август | 14,2 | 42,0 | 14,10 | 55,6 | 13,90 | 14,08 |
| сентябрь | 14,1 | 42,3 | 14,17 | 56,1 | 14,03 | 14,16 |
| октябрь | 14,2 | 42,5 | 14,20 | 56,5 | 14,13 | 14,23 |
| ноябрь | 14,3 | 42,6 | 14,30 | 56,8 | 14,20 | - |
| декабрь | 14,4 | 42,9 | - | 57,0 | 14,25 | - |

