Система нормальных уравнений для данного примера имеет вид:
             
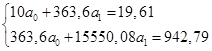
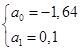
Следовательно, .
Значения  в таблице 51 получены путем подстановки значений факторного признака х_i(загрузка компьютера) в уравнение регрессии . На рисунке 32 полученные нами расчетные значения нанесены на диаграмму рассеяния, соединены между собой и образуют прямую линию, обозначающую область концентрации облака точек, построенных по исходным значениям х и у.

 



 

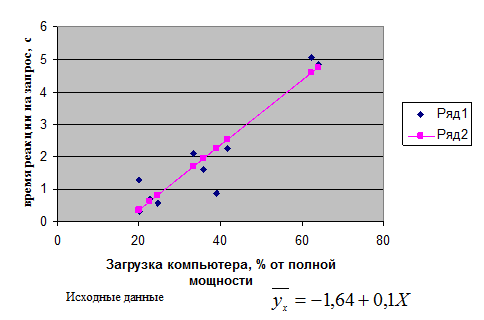
Рис. 32. Зависимость скорости реакции компьютера от состояния его загрузки

 

Проиллюстрируем расчет параметров линейного уравнения регрессии при помощи МS Excel.

 



 

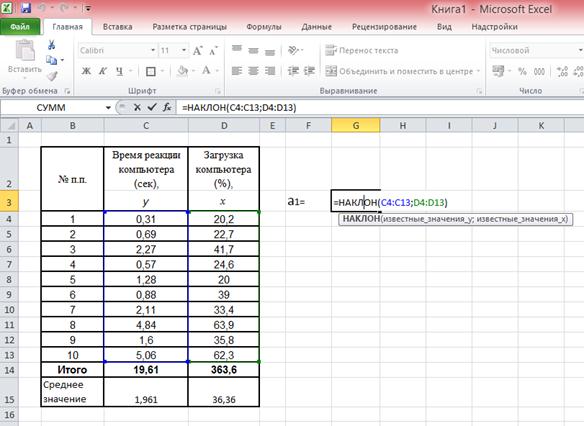
Рис. 33. Иллюстрация применения команды-функции «НАКЛОН» в MS Excel для расчета коэффициента регрессии а₁

 

На рисунке 33 показано, что пользователь рассчитывает значение коэффициента регрессии а₁ в ячейке G3. Для этого он предварительно ввел исходные данные в таблицу (столбцы С и D), затем кликнул на ячейку G3, ввел с клавиатуры «=НАКЛОН(», далее, следуя подсказкам Excel, указал известные значения y – это диапазон (С4:С13), затем указал известные значения x – диапазон (D4:D13), после этого ввел с клавиатуры символ «)» (чтобы соблюсти синтаксис команды). Ему остается только нажать клавишу Enter, чтобы увидеть на экране искомое значение коэффициента.

На рис. 34, иллюстрирующем пример расчета коэффициента а₀ в MS Excel, видно, что значение коэффициента регрессии а₁ – содержимое ячейки G3 – составляет 0,10.

 



 

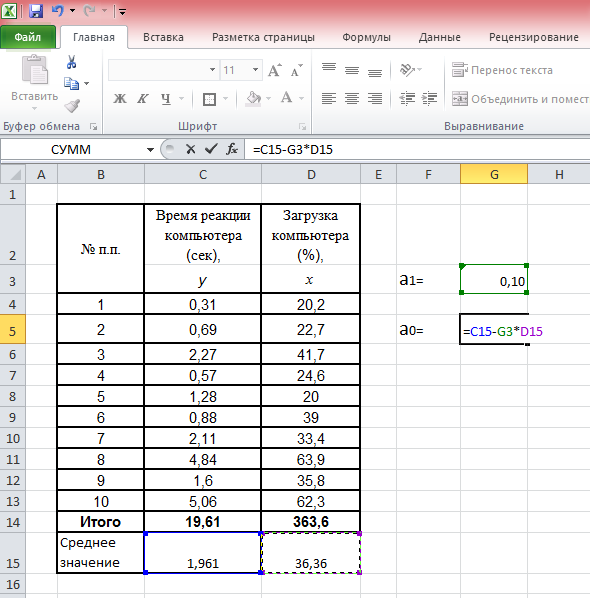
Рис. 34. Иллюстрация расчета параметра а₀ в MS Excel после применения команды-функции «НАКЛОН» для расчета коэффициента регрессии а₁

 

Величина а

---

₁ необходима для расчета параметра а₀ по формуле . Из рисунка 34. видно, что пользователь предварительно рассчитал средние значения показателей y и х и перешел к расчету коэффициента а₀ в ячейке G5. Он ввел в эту ячейку символ «=» и согласно формуле задал Excel последовательность действий: «возьми содержимое ячейки C15 (среднее значение y), вычти из него произведение ячейки G3 (коэффициент a₁) на ячейку D15 (среднее значение х)». Значение коэффициента а₀ составляет -1,64, следовательно:

Коэффициент регрессии a₁ = 0,1 означает, что при увеличении загрузки компьютерных мощностей на 1 % время реакции компьютера повышается в среднем на 0,1 сек.

Данную оценку связи можно использовать для прогнозирования времени реакции компьютерапри соответствующем проценте загрузке. Например, при загрузке компьютера на 50 % время его реакции составит  сек.

Линейные модели являются основными при определении аналитического выражения связи. Однако встречаются и нелинейные связи, хорошо описываемые параболой, гиперболой и т.д. Если связь между факторным и результативным признаками описывается уравнением параболы второго порядка вида:

,           (81)
то система нормальных уравнений имеет вид:

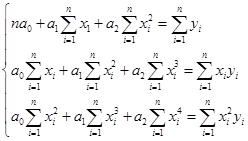       (82)

Оценка обратной связи осуществляется на основании гиперболы вида:
            (83)
Система нормальных уравнений для нахождения параметров гиперболы:

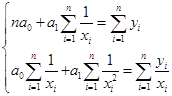             (84)


При нелинейной зависимости между признаками для измерения тесноты связи между ними вычисляют теоретическое корреляционное отношение:

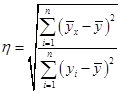             (85)


Корреляционное отношение изменяется в пределах от 0 до 1

---

. Его величина интерпретируется по стандартным критериям оценки коэффициента корреляции.
Пример 3. Рассмотрим данные об объеме производства вишни в фермерских хозяйствах и цене вишни.

 

Таблица 52.

 

Объем производства и фермерская цена вишни хозяйств области

 

№ п/п	Объем производства, тыс. т	Фермерская цена, тыс. долл. за т
1.	0,204	0,267
2.	0,260	0,174
3.	0,287	0,140
4.	0,239	0,208
5.	0,208	0,225
6.	0,218	0,243
7.	0,394	0,227
8.	0,266	0,166
9.	0,276	0,163
10.	0,404	0,262
11.	0,331	0,126
12.	0,373	0,165
13.	0,200	0,299
14.	0,198	0,325
15.	0,356	0,150
16.	0,384	0,188

 


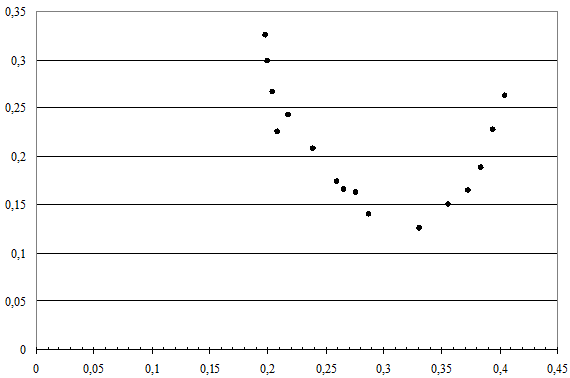
Рис. 35. Диаграмма рассеяния, характеризующая взаимосвязь между объемом производства вишни и фермерской ценой на нее
Как правило, зависимость между производством и ценой товара нелинейная. Диаграмма рассеяния, представленная на рис. 35, иллюстрирует пример нелинейной взаимосвязи, выраженной уравнением параболы второго порядка. Построим расчетную таблицу для определения параметров нелинейного уравнения регрессии, выраженного параболической функцией (табл. 53).
Таблица 53.

 

Расчетная таблица для нахождения параметров уравнения регрессии

 

Объем производства, тыс. т, xi	Фермерская цена, тыс. долл. за т, yi	хi2	хi3	хi4	xiyi	хi2yi
0,204	0,267	0,042	0,008	0,002	0,054	0,011	0,234
0,260	0,174	0,068	0,018	0,005	0,045	0,012	0,221
0,287	0,140	0,082	0,024	0,007	0,040	0,012	0,213
0,239	0,208	0,057	0,014	0,003	0,050	0,012	0,226
0,208	0,225	0,043	0,009	0,002	0,047	0,010	0,233
0,218	0,243	0,048	0,010	0,002	0,053	0,012	0,231
0,394	0,227	0,155	0,061	0,024	0,089	0,035	0,177
0,266	0,166	0,071	0,019	0,005	0,044	0,012	0,219
0,276	0,163	0,076	0,021	0,006	0,045	0,012	0,216
0,404	0,262	0,163	0,066	0,027	0,106	0,043	0,174
0,331	0,126	0,110	0,036	0,012	0,042	0,014	0,200
0,373	0,165	0,139	0,052	0,019	0,061	0,023	0,185
0,200	0,299	0,040	0,008	0,002	0,060	0,012	0,235
0,198	0,325	0,039	0,008	0,002	0,064	0,013	0,235
0,356	0,150	0,127	0,045	0,016	0,053	0,019	0,191
0,384	0,188	0,147	0,056	0,022	0,072	0,028	0,181
4,5979	3,328	1,407	0,455	0,154	0,927	0,278	3,371

---

Система нормальных уравнений для данного примера имеет вид (согласно формуле 82):

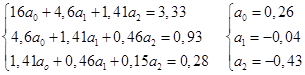
Следовательно, .

Значения  в таблице 53 получены путем пошаговой подстановки значений факторного признака х_i(объем производства вишни) в уравнение регрессии. Коэффициент регрессии a₁ = -0,04 означает, что при увеличении объема производства вишни на 1 тыс. т фермерская цена будет в среднем снижаться на 0,04 тыс. долл.
Определим тесноту связи между объемом производства и фермерской ценой вишни. Все расчеты представим во вспомогательной табл. 54.
Таблица 54.

 

Расчетная таблица для определения теоретического корреляционного отношения

 

yi
0,267	0,234	0,026	0,067	0,059	0,348
0,174	0,221	0,013	0,016	-0,034	0,116
0,140	0,213	0,005	0,003	-0,068	0,462
0,208	0,226	0,018	0,032	0,000	0,000
0,225	0,233	0,025	0,063	0,017	0,029
0,243	0,231	0,023	0,052	0,035	0,123
0,227	0,177	-0,030	0,093	0,019	0,036
0,166	0,219	0,011	0,012	-0,042	0,176
0,163	0,216	0,008	0,006	-0,045	0,203
0,262	0,174	-0,030	0,119	0,054	0,292
0,126	0,200	-0,010	0,010	-0,082	0,672
0,165	0,185	-0,020	0,051	-0,043	0,185
0,299	0,235	0,027	0,072	0,091	0,828
0,325	0,235	0,027	0,074	0,117	1,369
0,150	0,191	-0,020	0,028	-0,058	0,336
0,188	0,181	-0,030	0,071	-0,020	0,040
Итого		-	0,766	-	5,215

---

 

Теоретическое корреляционное отношение согласно формуле 85 составит:

Таким образом, связь между объемом производства вишни и фермерской ценой можно признать умеренной. Невысокое значение теоретического корреляционного отношения в данном случае оправдано, поскольку кроме объема производства на устанавливаемую фермерами цену оказывают сильное влияние другие факторы (уровень производственных издержек, конъюнктура спроса, цены конкурентов и др.).

Интерпретация моделей регрессии начинается со статистической оценки уравнения регрессии в целом и оценки входящего в модель факторного признака. Прежде всего, необходимо оценить коэффициенты регрессии. Чем больше величина коэффициента регрессии, тем значительнее влияние данного признака на моделируемый.

Знаки коэффициентов регрессии говорят о характере влияния на результативный признак. Если коэффициент регрессии при факторном признаке имеет знак «плюс», то с увеличением данного фактора результативный признак возрастает; если знак «минус», то с ростом значений этого факторного признака значения результативного признака уменьшаются.

Если экономические процессы подсказывают, что факторный признак должен иметь положительное значение, а он имеет знак «минус», то необходимо проверить расчеты параметров уравнения регрессии. Такое явление чаще всего бывает в силу допущенных ошибок при вычислении.

С целью расширения возможностей экономического анализа используются коэффициенты эластичности, определяемые по формуле:

,              (86)
где

 – среднее значение соответствующего факторного признака;

 – среднее значение результативного признака;

a₁ – коэффициент регрессии при соответствующем факторном признаке.
Коэффициент эластичности показывает, на сколько процентов в среднем изменится значение результативного признака при изменении факторного признака на 1 %.

 

Пример 4. Определим коэффициент эластичности по данным примера 73.

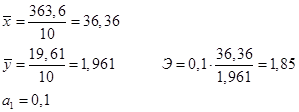
Таким образом, при увеличении загрузки мощности компьютера на 1 % время реакции соответственно увеличится на 1,85 %.

---

Смотрите также файлы

• Классный частренинг Мотивация учения.pdf

• 2. Письменно ответьте на вопросы Понятие об антропогенном кризисе и катастрофе.doc

• Решение Определим фондоотдачу (фотд) Фотд 42000 16000 2,625 тыс руб.docx

• Методические указания по выполнению лабораторной работы по дисциплине Теплофизика для студентов направления 20. 03. 01 Техносферная безопасность.pdf

• Фгбоу во ниу мэи.docx