ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 03.05.2024
Просмотров: 179
Скачиваний: 0
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.

Рис. 40. Динамика объема оказанных платных услуг населению региона по месяцам 2012 г.
Вопрос 4. Простейшие методы прогнозирования.
Анализ динамики социально-экономических явлений, выявление и характеристика основной тенденции развития дают основание для прогнозирования – определения будущих размеров уровня экономического явления.
Процесс прогнозирования предполагает, что закономерность развития, действующая в прошлом (внутри ряда динамики), сохранится и в прогнозируемом будущем, то есть прогноз основан на экстраполяции. Экстраполяция, проводимая в будущее, называется перспективой, а в прошлое – ретроспективой. Обычно, говоря об экстраполяции рядов динамики, подразумевают чаще всего перспективную экстраполяцию.
К простейшим методам экстраполяции относятся: прогнозирование на основе среднего абсолютного прироста, прогнозирование на основе среднего темпа роста и экстраполяция на основе применения метода аналитического выравнивания.
Прогнозирование по среднему абсолютному приросту может быть выполнено в том случае, если есть уверенность считать общую тенденцию линейной, то есть метод основан на предположении о равномерном изменении уровня (под равномерностью понимается стабильность абсолютных приростов).
Прогнозирование по среднему темпу роста можно осуществлять в случае, когда есть основание считать, что общая тенденция ряда характеризуется показательной (экспоненциальной) кривой. Для нахождения прогнозного значения на k шагов вперед указанными методами необходимо использовать следующие формулы:
Таблица 64.
Формулы расчета прогнозных значений простейшими методами прогнозирования
| Вид прогнозирования | Формула расчета |
| На основе среднего абсолютного прироста | |
| На основе среднего темпа роста | |
| Обозначения: Уn – фактическое значение конечного уровня ряда; – прогнозная оценка значения (i + k) уровня ряда; k – период упреждения (срок) прогноза; – значение среднего абсолютного прироста, рассчитанное по исходному ряду динамики (y1; y 2; y 3; …; y n); – средний темп роста, рассчитанный по исходному ряду динамики (y 1; y 2; y 3; …; y n). | |
Пример 4. По данным об объеме оказанных платных услуг населению региона (табл. 63) по месяцам 2012 г. построим помесячный прогноз на I квартал 2013 г. методом среднего абсолютного прироста и методом среднего темпа роста. Для наглядности расчетов представим начальные и конечные уровни, необходимые для расчета среднего абсолютного прироста и среднего темпа роста, в таблице 65.
Таблица 65.
Фрагмент ряда динамики объема оказанных платных услуг населению региона по месяцам 2012 г. (по данным табл.62)
| Месяцы | январь | февраль | … | ноябрь | декабрь |
| Объем оказанных платных услуг населению, млн.руб. | 13,3 | 13,4 | … | 14,3 | 14,4 |
Для получения прогнозных значений методом среднего абсолютного прироста:
1) определим средний абсолютный прирост:
2) по формуле 93 рассчитаем прогнозные значения для следующих трех периодов:

3) определим средний темп роста по формуле:
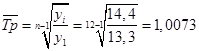
4) используя формулу 94, рассчитаем прогнозные значения для следующих трех периодов:
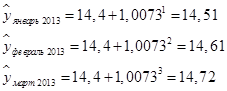
Для удобства сравнения объединим результаты прогнозирования в таблице 66.
Таблица 66.
Прогнозные значения объемов платных услуг населению региона по месяцам I квартала 2013 г. (млн руб.)
| Месяцы I квартала 2013 г. | k | Прогнозные значения, млн руб. | |
| методом среднего абсолютного прироста | методом среднего темпа роста | ||
| январь | 1 | 14,5 | 14,51 |
| февраль | 2 | 14,6 | 14,61 |
| март | 3 | 14,7 | 14,72 |
К недостаткам рассмотренных методов следует отнести то, что они учитывают лишь конечный и начальный уровни ряда, исключая влияние промежуточных уровней. Тем не менее методы среднего абсолютного прироста и среднего темпа роста имеют весьма широкую область применения, что объясняется простотой их вычисления.
Наиболее распространенным методом прогнозирования является расчет прогнозных значений показателя на основе аналитического выражения тренда. При этом для выхода за границы исследуемого периода достаточно продолжить значения переменной времени (t). Как правило, для целей прогнозирования расчет параметров уравнения тренда осуществляют, вводя значения фактора времени (t) линейно.
Пример 5. По данным о динамике объема оказанных населению платных услуг по месяцам 2012 г. (млн руб., табл. 67.) построим помесячный прогноз на 1 квартал 2013 г. методом экстраполяции тренда.
Таблица 67.
Таблица исходных и расчетных данных аналитического выравнивания ряда динамики объема оказанных платных услуг населению региона по месяцам 2012 г.
(значения фактора времени t заданы линейно)
| месяц | Объем оказанных услуг, млн руб., yi | ti | ti2 | уi * ti | yt |
| 1 | 13,3 | 1 | 1 | 13,3 | 13,3 |
| 2 | 13,4 | 2 | 4 | 26,8 | 13,4 |
| 3 | 13,5 | 3 | 9 | 40,5 | 13,5 |
| 4 | 13,4 | 4 | 16 | 53,6 | 13,6 |
| 5 | 13,6 | 5 | 25 | 68 | 13,7 |
| 6 | 13,8 | 6 | 36 | 82,8 | 13,8 |
| 7 | 14,0 | 7 | 49 | 98 | 13,9 |
| 8 | 14,2 | 8 | 64 | 113,6 | 14,0 |
| 9 | 14,1 | 9 | 81 | 126,9 | 14,1 |
| 10 | 14,2 | 10 | 100 | 142 | 14,2 |
| 11 | 14,3 | 11 | 121 | 157,3 | 14,3 |
| 12 | 14,4 | 12 | 144 | 172,8 | 14,4 |
| Итого | 166,2 | 78 | 650 | 1095,6 | 166,2 |
Построим линейную модель тренда вида:


Следовательно,
Для получения прогнозных значений методом аналитического выравнивания необходимо в полученную модель подставить значения фактора времени t для прогнозируемых месяцев. Продлевая ряд t, узнаем, что для января 2013 г. t = 13, для февраля 2013 г. t = 14, а для марта t = 15. Прогнозные значения представим в табл. 68.
Таблица 68.
Прогнозные значения объема платных услуг населению на I квартал 2013 г. (по месяцам, млн руб.)
| Месяцы I квартала 2013 г. | ti | Прогнозные значения, полученные методом аналитического выравнивания |
| январь | 13 | |
| февраль | 14 | |
| март | 15 | |
Вопросы для самопроверки:
1. Что такое ряды динамики? Какие виды рядов динамики вы знаете?
2. Что означает несопоставимость уровней рядов динамики и из-за чего она возникает?
3. Что характеризует: абсолютный прирост, темп роста, темп прироста? В чем разница между этими показателями?
4. Какой показатель является обобщающим показателем абсолютной скорости изменения явления во времени?
5. Что такое тенденция ряда динамики?
6. Для чего применяют метод скользящих средних? В чем основные преимущества и недостатки его использования?
7. В чем состоят исходные предпосылки применения метода аналитического выравнивания?
8. Что такое тренд и уравнение тренда?
9. Какой прием используют для упрощения расчетов параметров уравнения тренда при аналитическом выравнивании ряда динамики?
10. Какие методы экстраполяции вам известны, как они реализуются?
Литература по теме:
Основная литература:
1. Улитина Е.В. Статистика: учеб. пособие / Е.В. Улитина, О.В. Леднева, О.Л. Жирнова. – 3-е изд. – М.: МФПУ, 2013.– 312 с. – (Университетская серия).
Дополнительная литература:
1. Общая теория статистики: статистическая методология в изучении коммерческой деятельности: учебник / Под ред. А.А. Спирина, О.Э. Башиной. – М.: Финансы и статистика, 2004.
2. Практикум по теории статистики: учеб. пособие / Под ред. проф. Р.А. Шмойловой. – М.: Финансы и статистика, 2004.
3. Шмойлова Р.А., Минашкин В.Г., Садовникова Н.А., Шувалова Е.Б. Теория статистики: учебник / Под ред. проф. Р.А. Шмойловой. – М.: Финансы и статистика, 2004.
4. Методологические положения по статистике. – М.: Госкомстат России, 2010.
Практические задания.
Задание 1.
Имеются следующие данные о размерах страховых выплат страховых организаций РФ за период 2005–2011 гг. (трлн руб.):
| Годы | Страховые выплаты, трлн руб. | | | | | |||
| | | | | | | | ||
| 2007 | 486,6 | | | | | | | |
| 2008 | 633,2 | | | | | | | |
| 2009 | 739,9 | | | | | | | |
| 2010 | 774,8 | | | | | | | |
| 2011 | 902,2 | | | | | | | |

