• 
  декомпозируемость (возможность структуризации системы критериев). Критериев должно быть не более 7, поэтому если анализируемая ситуация такова, что должна оцениваться с помощью слишком боль­шого числа критериев, то целесообразно разбить их (разложить) на более мелкие группы для удобства одновременной работы с ними;
  

• достаточность (отсутствие избыточности). Критерии должны быть неизбыточны. Избыточность возникает за счет одновременного рассмотрения как критериев, характеризующих получаемые результаты, так и средств их достижения; В набор критериев для оценки анализируемой ситуации целесообразно включать лишь те критерии, без которых такая оценка невозможна. Этот принцип также направлен на то, чтобы процедура многокритериального оценивания не была без необходимости слишком громоздкой.

• минимальность (набор критериев должен быть минимально необходимым для осуществления оценки);

• измеримость (каждый критерий должен давать количественную или качественную оценку степени достижения цели).

Применение однокритериальных моделей принятия оптимальных управленческих решений в прикладном исследовании заключается в следующем.

Оптимизация экономических процессов – комплекс методов, которые позволяют выбрать из многих возможных вариантов использования ресурсов один – с точки зрения получения наилучших результатов. Постановка задач оптимизации возможна при условии выделения определенных предпосылок в отношении характера анализируемых экономических процессов.

В качестве важнейшей предпосылки выделяется наличие единого критерия оптимизации качества экономических решений, который может быть количественно измерен. При этом критерий оптимальности рассматривается как показатель, выражающий предельную меру экономического эффекта принимаемого решения для сравнительной оценки возможных решений и выбора наилучшего из них.

Этапы постановки оптимизационной задачи:

1. Уясняем задачу - ее экономический смысл. На этой основе

устанавливаем цель решения.

2. Оцениваем экономическую ситуацию - определяем, от

чего зависит достижение установленной цели.

3. Выбираем численный показатель, от которого достижение

цели зависит в первую очередь.

4. Выбираем метод решения. Строим математическую модель операции, устанавливающую количественные зависимости избранного показателя от условий задачи (подбираем соответствующий математический метод).

---

5. С помощью математической модели и найденного метода решаем задачу.

6. Проверяем правильность найденного решения.

Общая формулировка задачи оптимизации производственной программы заключается в следующем: определить оптимальный план производства продукции, учитывающий имеющееся обеспечение материальными, трудовыми, финансовыми ресурсами и занимаемую долю рынка. План считается оптимальным по заранее выбранному критерию.

В практической постановке задачи оптимизации производственной программы встречаются различные варианты критериев оптимальности и ограничений.

В качестве критериев оптимальности могут быть использованы следующие показатели:

1. Максимум выпуска продукции: , где

j – индекс вида продукции,

n – количество видов продукции,

- объем выпуска j-той продукции.

Данный критерий на практике применяется редко и может использоваться для завоевания доли рынка.

2 Максимум выпуска продукции в стоимостном выражении: 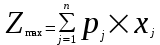, где 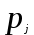- цена j-той продукции.

3. Максимум прибыли:

где - прибыль на единицу j-й продукции.

4. Минимум затрат:

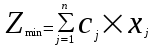
где – себестоимость производства единицы j- той продукции.

При постановке частных задач или задач по подразделениям промышленного предприятия в качестве критерия оптимальности могут быть использованы и другие критерии, позволяющие экономить отдельные виды ресурсов.

В рамках настоящего курса мы рассматриваем задачи по оптимизации производственной программы с применением одного критерия оптимальности. Для решения задач многокритериальной оптимизации возможно решение нескольких частных задач отдельно на каждый критерий оптимальности с последующим выбором компромиссного варианта.

Перейдем к рассмотрению системы ограничений. В модели формирования производственной программы выделяют три основные группы ограничений: ресурсные ограничения; ограничения по объему выпускаемой продукции (объемные ограничения); ограничения по технико–экономическим показателям.

---

Ресурсные ограничения отражают ограниченность различных факторов производства – оборудования, материальных, трудовых и др. ресурсов.

Ограничения по оборудованию – отражают максимальное количество часов работы по группам оборудования и могут быть выражены в следующей форме:

( )

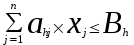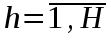где 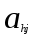- нормы затрат времени работы h-той группы оборудования по производству единицы j- того вида продукции,

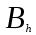- эффективный фонд времени работы h-той группы оборудования,

- объем производства j – той продукции (в натуральном выражении).

Ограничения по материальным ресурсам – учитывают лимит ресурсов по отдельным видам сырья и материалов:

( ) ,

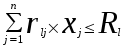где 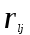- норма расхода - го вида сырья и материалов на производство единицы j – того вида продукции,

- наличие ( лимит ) сырья и материалов.

Ограничения по трудовым ресурсам : ( )

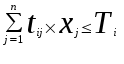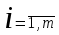где 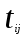- норма времени, затрачиваемая i – той профессиональной группой на производство единицы j – той продукции.

- реальный фонд времени группы рабочих i- той специальности (расчитывается исходя из баланса рабочего времени одного рабочего).

Важность объемных ограничений определяется необходимостью учета при формировании производственной программы спроса на производимую предприятием продукцию.

Форма записи может быть: или

где

---

– объем производства j – той продукции;

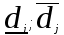– нижний и верхний пределы спроса на j- тый вид продукции.

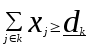
Если спрос задается по укрупненной номенклатуре, а промышленное предприятие определяет для себя объемные параметры выпуска по более детализированной номенклатуре, то ограничение по спросу принимает следующий вид: или

где - нижний и верхний пределы спроса на k-тую номенклатурную группу.

Примеры формализованной записи модели оптимизации представлены ниже.



Пример постановка задачи.

Цех выпускает три вида изделий. Производственные возможности цеха характеризуются следующими данными:

• 
  суточный фонд времени работы оборудования ­ 780 часов;
  
• 
  суточный расход сырья 850 тонн;
  
• 
  суточный расход электроэнергии 790 кВт-час.
  

Нормы затрат производственных ресурсов на единицу различных изделий приведены в следующей таблице:


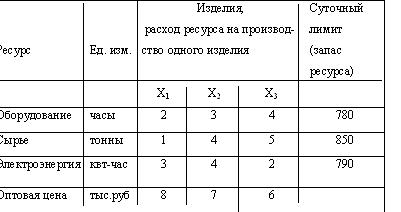
Требуется составить план производства, обеспечивающий наибольший по стоимости выпуск продукции. Математическая модель задачи имеет вид:
Формализованная экономико-математической модель:

Для решения задач линейного программирования существует универсальный метод – симплекс-метод, который может быть, в частности, реализован в EXCEL с помощью надстройки «Поиск решения». Важное значение имеет не только решение с целью получения вычисленных значений переменных, но и анализ полученных результатов и устойчивость найденного решения к возможным изменениям внутренних и внешних условий. Решение в среде EXCEL имеет вид:




Решение задачи представлено на листе Excel «Пример решения задач Лекция 5» данной дисциплины.

На основе результатов решения необходимо сформировать два вида отчетов- Отчет по результатам и Отчет по устойчивости, представленные ниже.

---

Экономическая интерпретация результатов и исследование устойчивости оптимального решения.

Рассмотрим интерпретацию результатов реализации в ЕXCEL задачи формирования производственной программы на примере модели рассмотренной задачи.

Основные результаты решения задачи содержатся в двух отчетах: отчете по результатам и отчете по устойчивости.

В отчет по результатам, состоящем из трех небольших таблиц, включаются конечные значения целевой функции и переменных, дополнительные сведения об ограничениях.

В отчете по устойчивости (состоит из двух маленьких таблиц) содержатся сведения о чувствительности полученного решения к малым изменениям коэффициентов целевой функции или в формулах ограничений.

Выводы по отчету по результатам. Оптимальным планом предусматривается выпуск только двух видов изделий: 1-го и 3-го вида в количестве 200 и 95 единиц соответственно.

При таком плане общая стоимость выпущенной продукции будет максимальной и составит 2170 тыс.руб. При этом фактическое использование ресурсов составит: по оборудованию – 780 часов, по сырью – 675 тонн, а по электроэнергии –790 квт-часов, т.е. ресурсы оборудования и электроэнергии используются полностью, а сырье недоиспользуется в объеме 175 тонн.

Выводы по отчету по устойчивости. Табличка «Изменяемые ячейки» содержит помимо результата решения задачи (колонка «Результирующее значение») нормированную стоимость единицы каждого вида изделия. Нормированная стоимость показывает, на какую величину изменится значение критерия оптимальности при увеличении объема выпуска данной продукции на одну единицу. Поскольку критерий (целевая функция) в данной задаче на максимум - то отрицательное значение теневой цены характеризует невыгодность продукции; если же теневая цена положительна ­ то соответствующая продукция выгодна. Невыгодной к выпуску является 2-ой вид изделия, выпуск каждой единицы 2-го изделия приведет к снижению значения целевой функции на 3,75 тыс.руб., поэтому выпуск этого вида изделия оптимальным планом не предусмотрен.

Три последних колонки содержат значение коэффициентов целевой функции (оптовая цена единицы каждого вида продукции) и предельные значения приращения целевых коэффициентов, при которых сохраняется найденное оптимальное решение. Например, допустимое увеличение цены на изделие 2-говида равно 3,75 тыс. руб/единицу, а допустимое уменьшение ­ практически неограниченно. Это означает, что если цена изделия второго вида вырастет более чем на 3,75 тыс. руб./единицу, то оптимальное решение изменится: станет целесообразным выпускать второй вид изделия. А если цена этого изделия будет снижаться вплоть до нуля, то оптимальное решение (200, 0, 95) останется прежним.

---

Смотрите также файлы

• Ответ н. 55555555 Автокорреляционная функция это функция от Автокорреляционная функция .doc

• Ответ на отлично. Автокорреляционная функция это функция от автокорреляционная функция .pdf

• Контрольная работа 2 по теме Степень с натуральным показателем. Одночлены. Многочлены. Сложение и вычитание многочленов.docx

• Заместитель прокурора Предельный возраст для пребывания в должности судьи кс рф.docx

• .docx