ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 05.05.2024
Просмотров: 16
Скачиваний: 0
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
РАСЧЕТНО-ГРАФИЧЕСКАЯ РАБОТА
Вариант 34
Общее задание.
1. Составить схему замещения электрической системы. Выбрать положительные направления токов ветвей.
2. Определить параметры схемы замещения.
3. Построить направленный граф сети. Выделить в нем дерево и хорды. Проверить правильность выделения дерева и хорд. Пронумеровать узлы и ветви в установленном порядке (базисный узел имеет последний номер).
4. Составить первую и вторую матрицы соединений.
Для задания 1.
5. Нагрузки представить в виде задающих токов.
6. Составить вектор задающих токов в узлах.
7. Составить матрицу сопротивлений ветвей.
8. Выполнить расчет установившегося режима сети указанным на основе обобщенного уравнения состояния.
9. Полученные в результате расчета токи ветвей и напряжения узлов нанести на граф сети. Уточнить направления ветвей по результатам расчета.
10. Проанализировать полученные результаты.
Для задания 2.
11. Нагрузки представить в виде задающих токов.
12. Изменить схему в соответствии с аварийным отключением Т2 и Л2.
13. Составить матрицу коэффициентов распределения дерева для разомкнутой сети.
14. Выполнить расчет послеаварийного режима на основе матрицы коэффициентов распределения.
15. Полученные в результате расчета токи ветвей и напряжения узлов нанести на граф сети. Уточнить направления ветвей по результатам расчета.
16. Проанализировать полученные результаты.
Анализ баланса мощности.
17. Нагрузки представить в виде мощностей.
18. На основании полученных токов в ветвях и напряжений в узлах определить мощности начала и конца каждой ветви, а также потери мощности в схеме.
19. Проанализировать уровни напряжения на участках схемы электроснабжения и уточнить фактические напряжения в узлах нагрузки с учетом коэффициента трансформации.
20. Нанести на граф сети мощности начала и конца ветви, а также напряжения узлов.
21. Проанализировать полученные результаты.
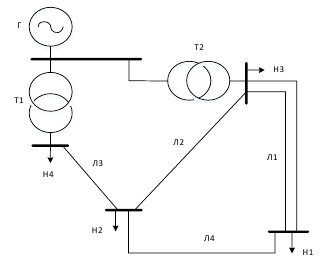
Дано:
Номинальное напряжение сети ВН, 110 кВ;
номинальное напряжение сети НН, 10 кВ;
ЛЭП 1 – АС-120: напряжение сети 110 кВ,
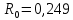Ом/км,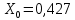 
Ом/км, длина – 17 км;
ЛЭП 2 – АС-150: напряжение сети 110 кВ,
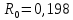Ом/км, 
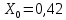Ом/км, длина – 16 км;ЛЭП 3 – АС-240: напряжение сети 110 кВ,
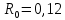Ом/км, 
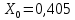Ом/км, длина – 20 км;ЛЭП 4 – АС-150: напряжение сети 110 кВ,
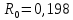Ом/км, 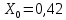Ом/км, длина –12 км;трансформатор Т1 - ТДН-16000: напряжение сети 35 кВ,
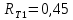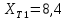Ом, 
Ом;трансформатор Т2 - ТРДН-40000: напряжение сети 35 кВ,
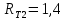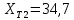Ом, 
Ом;мощности нагрузок:
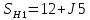МВА; 
МВ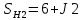А; 
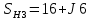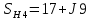МВА; 
МВА.Решение
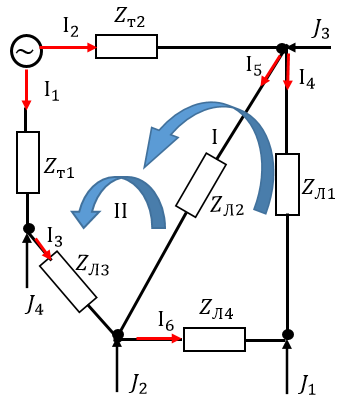
1-2. Построим схему замещения с учетом того что схемы замещения линии электропередач и трансформатора принимаются упрощенными, без учета параметров намагничивания, т.е. будет представлена только продольной ветвью – активным и индуктивным сопротивлениями.
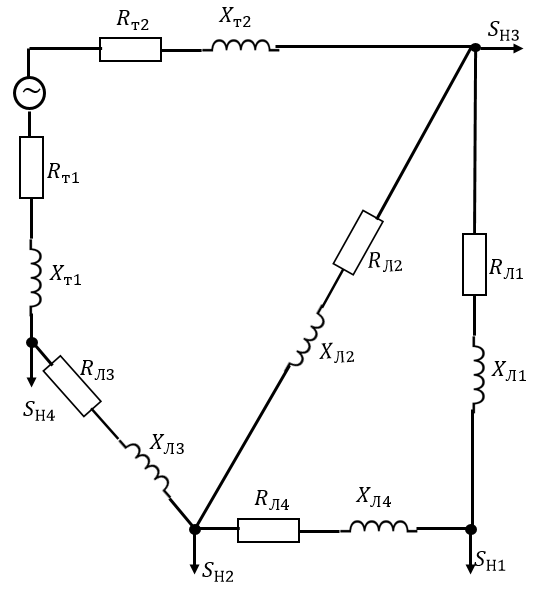
Упростим схему, для этого найдем активное и индуктивное сопротивления линий электропередачи и заменим резистор и катушку индуктивности комплексным сопротивлением по формулам:
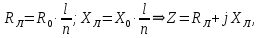
где
, 
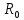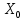– удельное активное и индуктивное сопротивления линии, Ом/км; 
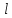– длина линии, км; 
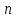– число цепей линии электропередачи: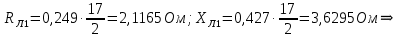
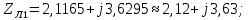
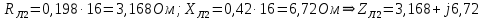
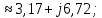
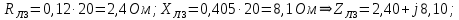
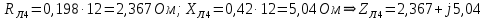
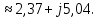
Комплексные сопротивления трансформаторов:
; 
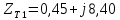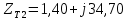.Получим упрощенную схему замещения, укажем на ней направления токов и выделим контуры:
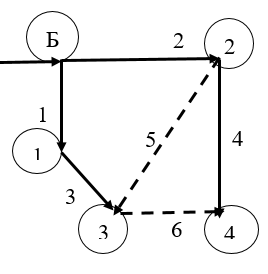
3. Построим направленный граф сети. Выделим в нем дерево и хорды (пунктиром). Пронумеруем узлы и ветви в установленном порядке (базисный узел имеет последний номер): в качестве базисного узла принимается узел, к которому подключен источник питания.
Порядок нумерации схем с учетом принципа ярусности:
а) последовательно числами натурального ряда на графе схемы нумеруются все ветви, берущие свое начало в балансирующем узле, и такие же номера присваиваются узлам (вершинам), которые являются концами этих ветвей (концом первой ветви должен быть узел 1, концом второй – узел 2, и т. д.). Эти ветви составят первый ярус схемы;
б) начиная с 1-й вершины графа, по аналогичному принципу выбираются и нумеруются ветви второго яруса, оттекающие от конечных вершин ветвей первого яруса, затем ветви третьего яруса, оттекающие от конечных вершин ветвей второго яруса и т.п. То есть, начальными вершинами ветвей последующего яруса служат концы ветвей предыдущего яруса, и рассмотрение узлов ведется в порядке возрастания их номеров.
Совокупность ветвей схемы, составляющих минимальный связанный подграф, обеспечивающий связь балансирующего узла со всеми n независимыми узлами схемы, образует так называемое дерево сети.
Когда в ходе нумерации встречается ветвь, подтекающая к ранее пронумерованному узлу
, то эта ветвь замыкает собой контур и называется хордой.
Проверим правильность выделения дерева и хорд:
- число ветвей, входящих в состав дерева схемы, на единицу меньше числа
узлов всей схемы:
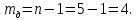
- число хорд равно числу независимых контуров схемы:
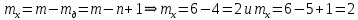. 4. Составить первую и вторую матрицы соединений.
Первая матрица соединений
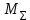– матрица соединений ветвей в узлах, число строк которой равно числу вершин графа (
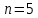), а число столбцов равно числу ребер (
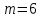). Элементы матрицы равны: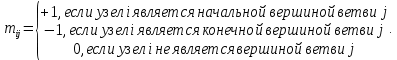
| = | |  |  |  |  |  |  |
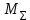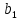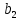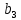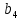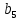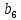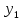 |  -1 | 0 | 1 | 0 | 0 | 0 | |
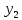 | 0 | -1 | 0 | 1 | 1 | 0 | |
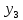 | 0 | 0 | -1 | 0 | -1 | 1 | |
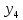 | 0 | 0 | 0 | -1 | 0 | -1 | |
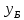 | 1 | 1 | 0 | 0 | 0 | 0 |
Проверка: сумма элементов в каждом столбце равна 0.
Вторая матрица соединений N – матрица соединений ветвей в независимые контуры, число строк которой равно числу независимых контуров
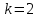, а число столбцов равно числу ветвей 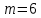. Элементы второй матрицы соединений получаются таким образом:
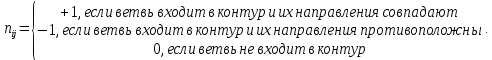
| N = | | | | | | | |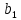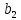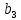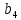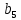
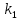 |  1 | -1 | 1 | -1 | 0 | 1 | |
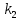 | 1 | -1 | 1 | 0 | -1 | 0 |
Задание 1.
5. Представим нагрузки в виде задающих токов по формуле:
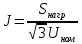
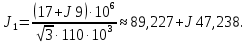
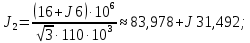
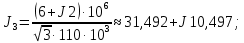
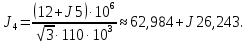
6. Составим вектор задающих токов в узлах:
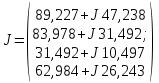
7. Составим матрицу сопротивлений ветвей:
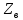 = |  0,45+j8,40 | 0 | 0 | 0 | 0 | 0 |
| 0 | 1,40+j34,70 | 0 | 0 | 0 | 0 | |
| 0 | 0 | 2,40+j8,10 | 0 | 0 | 0 | |
| 0 | 0 | 0 | 2,12+j3,63 | 0 | 0 | |
| 0 | 0 | 0 | 0 | 3,17+j6,72 | 0 | |
| | 0 | 0 | 0 | 0 | 0 | 2,37+j5,04 |
