---

9. Полученные в результате расчета токи ветвей и напряжения узлов нанесем на граф сети, уточнив направления ветвей по результатам расчета.


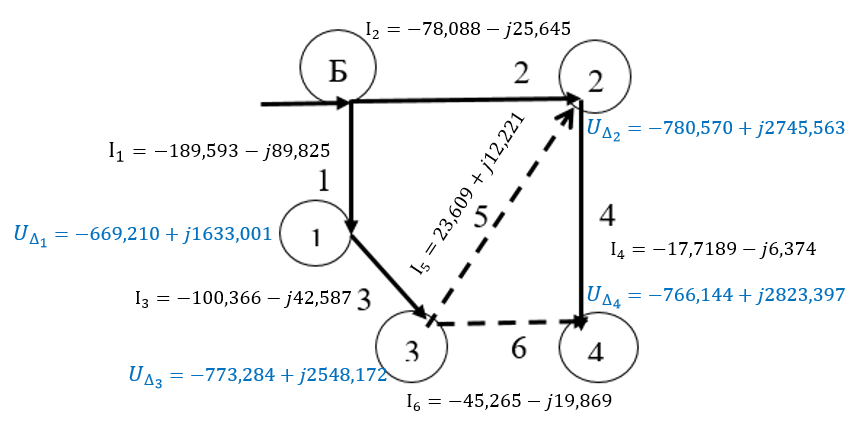
10. Проанализируем полученные результаты. Проверим правильность расчета:

- по первому закону Кирхгофа (по току в узлах):

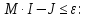
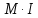=	-1	0	1	0		0	0		-189,593-j89,825		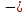89,227+J47,238	=
	0	-1	0	1		1	0		-78,088-j25,645		83,978+J31,492
	0	0	-1	0		-1	1		-100,366-j42,587		31,492+J10,497
	0	0	0	-1		0	-1		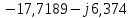		62,984+J26,243
									23,609+j12,221
									-45,265-j19,869
0

---

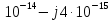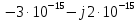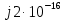выполняется с достаточно высокой точностью;

- по закону Ома (по напряжению в ветвях):

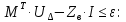
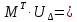	669,210-j1633,001
	780,570-j2745,563
	104,074-j915,171
	-14,425-j77,833
	-7,285+j197,391
	-7,140-j275,225

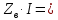	0,45+j8,40	0	0	0	0	0
	0	1,40+j34,70	0	0	0	0
	0	0	2,40+j8,10	0	0	0
	0	0	0	2,12+j3,63	0	0
	0	0	0	0	3,17+j6,72	0
	0	0	0	0	0	2,37+j5,04

669,210-j1633,001

780,570-j2745,563

104.,074-j915,171

-14,425-j77,833

-7,285+j197,391

-7,140-j275,225

выполняется с высокой степенью точности порядка 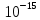. Следовательно, расчеты выполнены верно.

---

Задание 2.

1 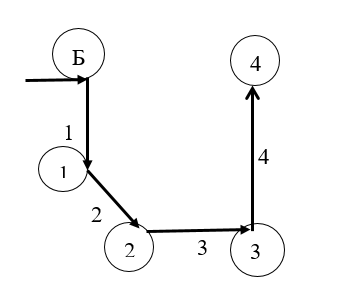1-12. Нагрузки представим в виде задающих токов и изменим схему в соответствии с аварийным отключением Т2 и Л2, построим граф сети: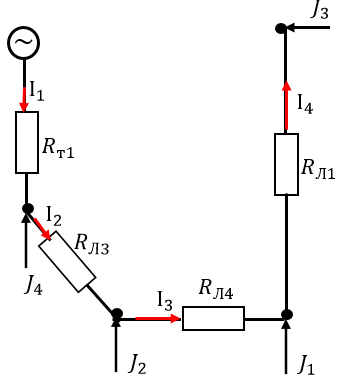



13. Составим матрицу коэффициентов распределения дерева для разомкнутой сети:

Матрица коэффициентов распределения 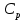является обратной к матрице 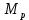и может быть получена непосредственно из направленного графа схемы:

- столбцы матрицы 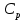отвечают узлам, а строки ветвям;

- двигаясь от первого узла к базисному, то есть по первому столбцу смотрят какие ветви встречаются на пути движения, при этом, если направление

движения совпадает с направлением ветви, то ставят (+ 1), если противоположно - (-1), если ветви не встречается на рассмотренном пути - (0).

=
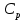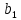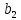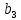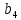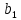		-1	-1	-1	-1
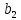		0	-1	-1	-1
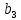		0	0	-1	-1
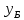		0	0	0	-1

---

	-1	-1	-1	-1		89,227+J47,238	=	-267,681-j115,47
	0	-1	-1	-1		83,978+J31,492		-178,454-j68,232
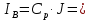	0	0	-1	-1		31,492+J10,497		-94,476-j36,74
	0	0	0	-1		62,984+J26,243		-62,984-J26,243

14. Выполнить расчет послеаварийного режима на основе матрицы коэффициентов распределения.

Найдем токи в ветвях:

Найдем узловые напряжения:

	-1	0	0	0	*
	-1	-1	0	0
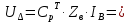	-1	-1	-1	0
	-1	-1	-1	-1

	0,45+j8,40	0	0	0		-267,681-j115,47
	0	2,40+j8,10	0	0		-178,454-j68,232	=
	0	0	2,37+j5,04	0		-94,476-j36,74
	0	0	0	2,12+j3,63		-62,984-J26,243

---

Смотрите также файлы

• Объектом исследования является экономический потенциал Республики Крым.docx

• Бизнесплан Открытие детского досугового центра.docx

• Экзаменационные вопросы по дисциплине для студентов дневного и заочного факультетов Интегрированный модуль Экономика.doc

• Тест раздел 1 Современные технологии формирования и развития детского коллектива.docx

• Збільшення рухомості та проникності при інєктуванні бетоних та цементних сумішей при використанні добавоксуперпластифікаторів.doc