ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 05.05.2024
Просмотров: 31
Скачиваний: 0
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
8. Выполним расчет установившегося режима сети указанным на основе обобщенного уравнения состояния:
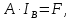
где
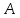 - объединенная матрица коэффициентов, которая включает в себя две матрицы
- объединенная матрица коэффициентов, которая включает в себя две матрицы 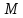 ,
, 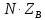 и имеет следующую структуру:
и имеет следующую структуру: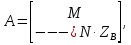
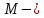 составляется из матрицы
составляется из матрицы 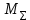 путем вычеркивания строки, соответствующей узлу баланса (последняя строка):
путем вычеркивания строки, соответствующей узлу баланса (последняя строка): 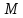 = = | | 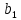 | 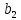 | 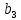 | 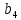 | 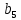 |  |
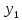 |  -1 -1 | 0 | 1 | 0 | 0 | 0 | |
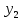 | 0 | -1 | 0 | 1 | 1 | 0 | |
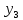 | 0 | 0 | -1 | 0 | -1 | 1 | |
 | 0 | 0 | 0 | -1 | 0 | -1 |
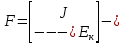 объединенная матрица свободных членов, включающая в себя:
объединенная матрица свободных членов, включающая в себя: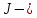 вектор задающих токов;
вектор задающих токов; 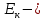 матрица контурных ЭДС, алгебраическая сумма ЭДС замкнутого контура.
матрица контурных ЭДС, алгебраическая сумма ЭДС замкнутого контура.При использовании обобщенного уравнения состояния расчет установившегося режима ЭЭС производится в следующем порядке: вначале определяются токи в ветвях схемы
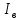 , а затем рассчитываются напряжения в узлах
, а затем рассчитываются напряжения в узлах 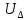 , падение напряжения в ветвях
, падение напряжения в ветвях 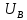 , потоки активной и реактивной мощностей и т.д.
, потоки активной и реактивной мощностей и т.д.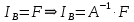
Запишем элементы матрицы
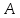 и найдем обратную ей матрицу:
и найдем обратную ей матрицу: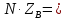
| = |  1 1 | -1 | 1 | -1 | 0 | 1 |
| 1 | -1 | 1 | 0 | -1 | 0 |
 |  0,45+j8,40 0,45+j8,40 | 0 | 0 | 0 | 0 | 0 |
| 0 | 1,40+j34,70 | 0 | 0 | 0 | 0 | |
| 0 | 0 | 2,40+j8,10 | 0 | 0 | 0 | |
| 0 | 0 | 0 | 2,12+j3,63 | 0 | 0 | |
| 0 | 0 | 0 | 0 | 3,17+j6,72 | 0 | |
| | 0 | 0 | 0 | 0 | 0 | 2,37+j5,04 |
| = |  0,45+ j8,4 | -1,4- j34,7 | 2,4+ j8,1 | -2,12- j3,63 | 0 | 2,37+ j5,04 |
| 0,45+ j8,4 | -1,4- j34,7 | 2,4+ j8,1 | 0 | -3,17- j6,72 | 0 |
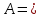 | -1 | 0 | 1 | 0 | 0 | 0 |
| 0 | -1 | 0 | 1 | 1 | 0 | |
| 0 | 0 | -1 | 0 | -1 | 1 | |
| 0 | 0 | 0 | -1 | 0 | -1 | |
 0,45+ j8,4 | -1,4- j34,7 | 2,4+ j8,1 | -2,12- j3,63 | 0 | 2,37+ j5,04 | |
| 0,45+ j8,4 | -1,4- j34,7 | 2,4+ j8,1 | 0 | -3,17- j6,72 | 0 |
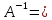 |  -0,848+j0,009 -0,848+j0,009 | -0,626-j0,044 | -0,698-j0,018 | -0,656-j0,031 | 0,001-j0,008 | 0,001-j0,010 |
| -0,152-j0,009 | -0,374+j0,044 | -0,302+j0,018 | -0,344+j0,031 | -0,001+j0,008 | -0,001+j0,010 | |
| 0,152+j0,009 | -0,626-j0,044 | -0,698-j0,018 | -0,656-j0,031 | 0,001-j0,008 | 0,001-j0,010 | |
| -0,066-j0,005 | 0,270+j0,025 | -0,131+j0,005 | -0,473+j0,003 | -0,026+j0,055 | 0,025-j0,048 | |
| -0,086-j0,004 | 0,356+j0,019 | -0,171+j0,013 | 0,129+j0,028 | 0,025-j0,048 | -0,026+j0,058 | |
| 0,066+j0,005 | -0,270-j0,025 | 0,131-j0,005 | -0,527-j0,003 | 0,026-j0,055 | -0,025+j0,048 | |
| | | | | | | |
Так как нагрузка и генерация мощности моделируются с помощью задающих токов, то ЭДС в ветвях отсутствует.

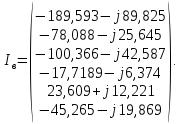
Найдем напряжения в узлах.
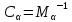 = = | -1 | 0 | 1 | 0 | -1 | = | -1 | 0 | -1 | 0 |
| 0 | -1 | 0 | 1 | | 0 | -1 | 0 |  -1 -1 | ||
| 0 | 0 | -1 |  0 0 | | 0 | 0 | -1 | 0 | ||
| 0 | 0 | 0 | -1 | | 0 | 0 | 0 | -1 |
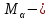 составлена из матрицы
составлена из матрицы 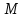 , вычеркиванием 5 и 6 столбца (хорд)
, вычеркиванием 5 и 6 столбца (хорд) 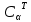 = = | -1 | 0 | 0 | 0 |
| 0 | -1 | 0 |  0 0 | |
| -1 | 0 | -1 | 0 | |
| 0 | -1 | 0 | -1 |
Запишем матрицу сопротивлений ветвей дерева:
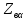 = = |  0,45+j8,40 0,45+j8,40 | 0 | 0 | 0 |
| 0 | 1,40+j34,70 | 0 | 0 | |
| 0 | 0 | 2,40+j8,10 | 0 | |
| 0 | 0 | 0 | 2,12+j3,63 |
Определяем узловые напряжения:
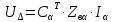
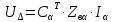 = = |  -0,45-j8,40 -0,45-j8,40 | 0 | 0 | 0 | 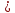 |
| 0 | -1,40-j34,70 | 0 | 0 | ||
| -0,45-j8,40 | 0 | -2,40-j8,10 | 0 | ||
| 0 | -1,40-j34,70 | 0 | -2,12-j3,63 |
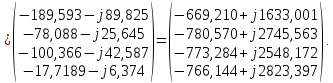
Определяем напряжения в ветвях:
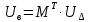
| | -1 | 0 | 0 | 0 |  | | = | 669,210-j1633,001 |
| | 0 | -1 | 0 | 0 | -669,210+j1633,001 | 780,570-j2745,563 | ||
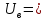 | 1 | 0 |  -1 -1 | 0 |  -780,570+j2745,563 -780,570+j2745,563 | 104,074-j915,171 | ||
| | 0 | 1 | 0 | -1 | -773,284+j2548,172 |  -14,425-j77,833 -14,425-j77,833 | ||
| | 0 | 1 | -1 | 0 | -766,144+j2823,397 | -7,285+j197,391 | ||
| | 0 | 0 | 1 | -1 | | -7,140-j275,225 |
