Файл: Решение задач 11 на нахождение наибольшего и наименьшего значения функции из егэ по математике.doc

Стационарными точками называются такие значения аргумента функции, при которых ее производная обращается в 0.

Область определения функции – это множество всех допустимых значений переменной . Геометрически – это проекция графика функции на ось .

Точки минимума и максимума называются точками экстремума.

Производной функции в данной точке называется предел отношения приращения функции в этой точке к приращению аргумента, при условии, что приращение аргумента стремится к нулю. Обозначение производной: или .

Тогда или

Значение функции в точке максимума называют максимумом функции.

Значение функции в точке минимума называют минимумом функции.

Приложение Б

Примеры тестовых заданий

1. 
   Как называют точки, в которых функция имеет производную, равную 0, или недифференцируема?
   

1. 
   Критическими точками этой функции
   
2. 
   Достаточными точками этой функции
   
3. 
   Точкой минимума функции
   
4. 
   Точкой максимума функции
   

2. 
   Как называется точка x0, если существует такая окрестность точки x0, что для всех x, не равных x0, из этой окрестности выполняется неравенство f(x)>f(x0)
   

1. 
   Точкой минимума
   
2. 
   Точкой максимума
   

3. 
   На рисунке изображен график производной функции f(x), определенной на интервале (-7;14), Найдите количество точек максимума функции f(x) на отрезке [-6;9]
   

---

1. 
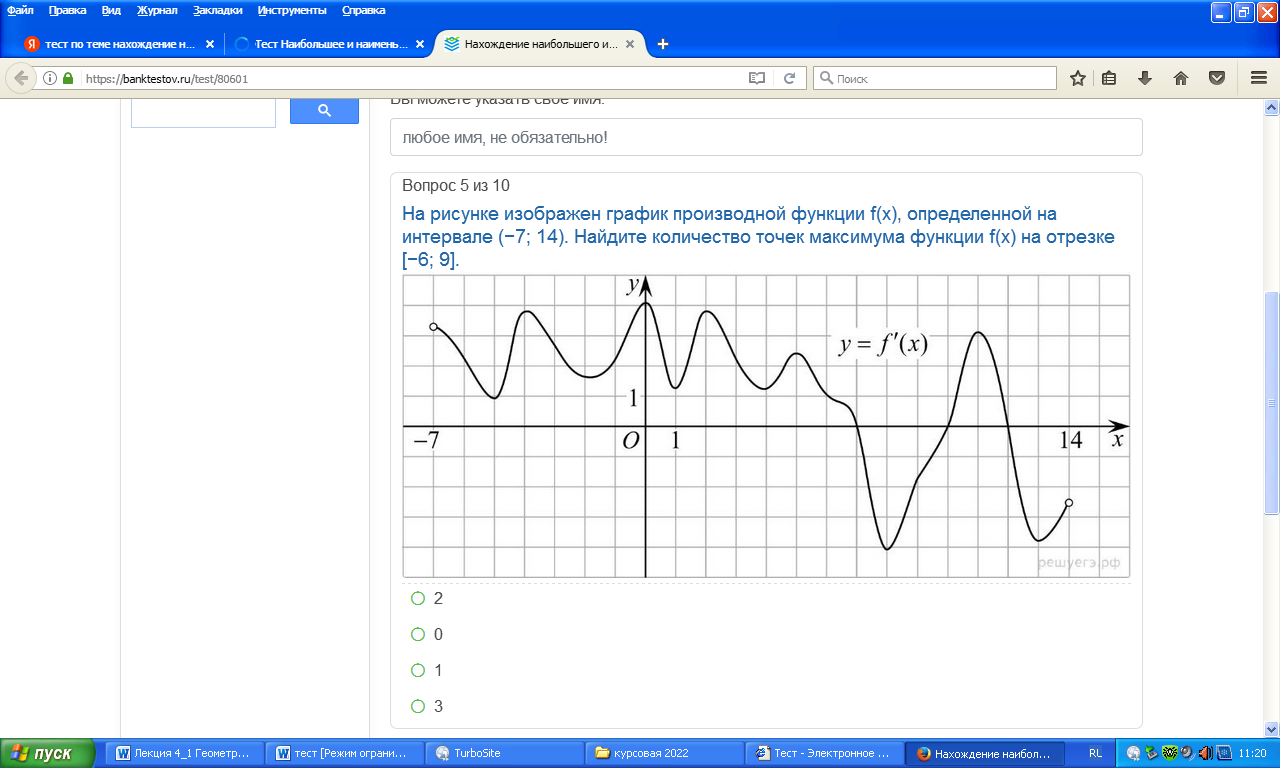
   2
   
2. 
   0
   
3. 
   1
   
4. 
   3
   

4. 
   Верно ли указан порядок действий при нахождении наибольшего и наименьшего значений функции f(x) на отрезке [a; b]:
   

1. 
   найти значения функции на концах отрезка, т.е. f(a) и f(b)
   
2. 
   найти значения функции в тех критических точках, которые принадлежат интервалу (a; b)
   
3. 
   из всех найденных значений выбрать наименьшее и наибольшее
   

1. 
   Да
   
2. 
   Нет
   

5. 
   На рисунке изображен график производной функции f(x), определенной на интервале (-8;4), В какой точке отрезка [-7;-3] f(x) принимает наименьшее значение?
   

1. 
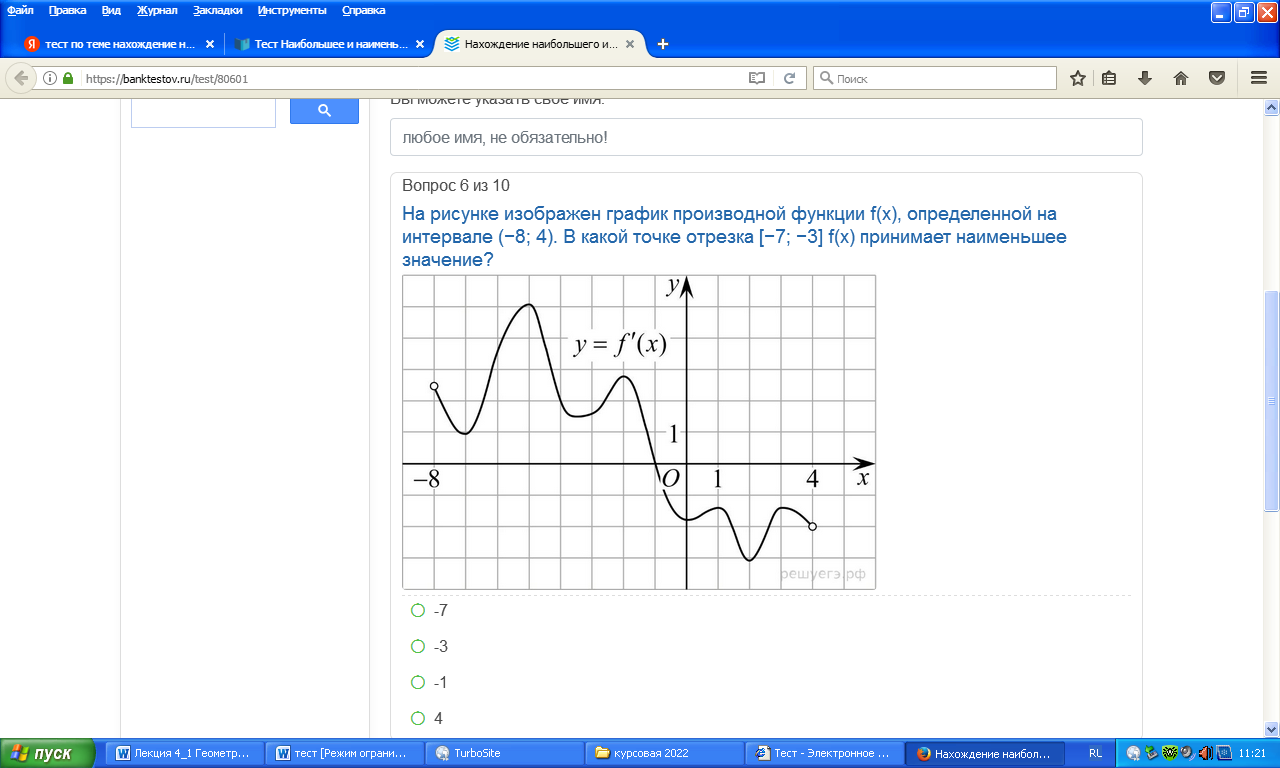
   -7
   
2. 
   0
   
3. 
   -1
   
4. 
   4
   

6. 
   Найти точку максимума функции .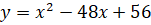
   

1. 
   -4
   
2. 
   4
   
3. 
   0
   
4. 
   1
   

7. 
   Найдите наименьшее значение функции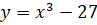 на отрезке [0;4].
   

1. 
   0
   
2. 
   4
   
3. 
   56
   
4. 
   -54
   

8. 
   Укажите лишние действия при нахождении наибольшего и наименьшего значения функции.
   

1. 
   Простроить график функции
   
2. 
   Найти экстремумы функции
   
3. 
   Найти модуль результата
   
4. 
   Найти производную функции
   

9. 
   Найти наибольшее значение функции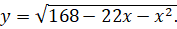
   

1. 
   0
   
2. 
   22
   
3. 
   17
   
4. 
   20
   

10.Найдите наибольшее значение функции на отрезке [-17; -8].

1. 
   900
   
2. 
   -90
   
3. 
   90
   
4. 
   99
   

---