Файл: Решение задач 11 на нахождение наибольшего и наименьшего значения функции из егэ по математике.doc

2.3. Подготовка и реализация в электронном виде материала для ЭОИ

Тема разрабатываемого электронного образовательного издания рассматривается в 11 классе, учащиеся сталкиваются с задачами на эту тему и различными методиками их решения. Во всех рассмотренных мной учебниках так или иначе фигурировала эта тема.

Несмотря на это, у учащихся все же часто возникают затруднения при решении задач, связано это с тем, что данной теме каждый учебный год выделяют минимальное количество часов, за которое не все дети успевают усвоить материал, а закрепление этой темы в дальнейших разделах почти не происходит.

Данное электронное образовательное издание разработано для усвоения и закрепления материала этой темы. Его можно считать универсальным помощником при подготовке к уроку, олимпиаде или ЕГЭ, так как в нем есть не только практические задания, но и обширный теоретический материал. С помощью него учащиеся смогут самостоятельно или с преподавателем на факультативных занятиях, изучить различные методики решения задач, а также закрепить полученные знания, пройдя тест и решив предложенные задачи, которых нет в школьном курсе математики.

Благодаря использованию программы TurboSite электронное образовательное издание получилось в виде сайта, понятного и удобного для использования. При открытии учебника перед пользователем открывается главная страница со всей необходимой информацией о нем, обложкой, сведениями об авторе и названии. Справа расположено оглавление, с помощью которого совершается переход от одного раздела к другому. Навигация по сайту осуществляется с помощью гиперссылок, что позволяет быстро и без проблем перемещаться.

Содержание учебника разработано в соответствии со стандартами, для того чтобы обучающийся мог постепенно переходить от одного этапа изучения темы к другому. Сам учебник делится на следующие основные части:

1. 
   Аннотация - содержащая краткое описание учебника.
   

---

Рисунок 1. - Аннотация

2. 
   Раздел 1 «Наибольшее и наименьшее значение функции».
   

Рисунок 2. – Теоретическая часть ЭОИ

3. 
   Раздел 2 «Решение прототипов задач № 11 из ЕГЭ по математике».
   

Рисунок 3. – Практическая часть ЭОИ

4. 
   Тест.
   

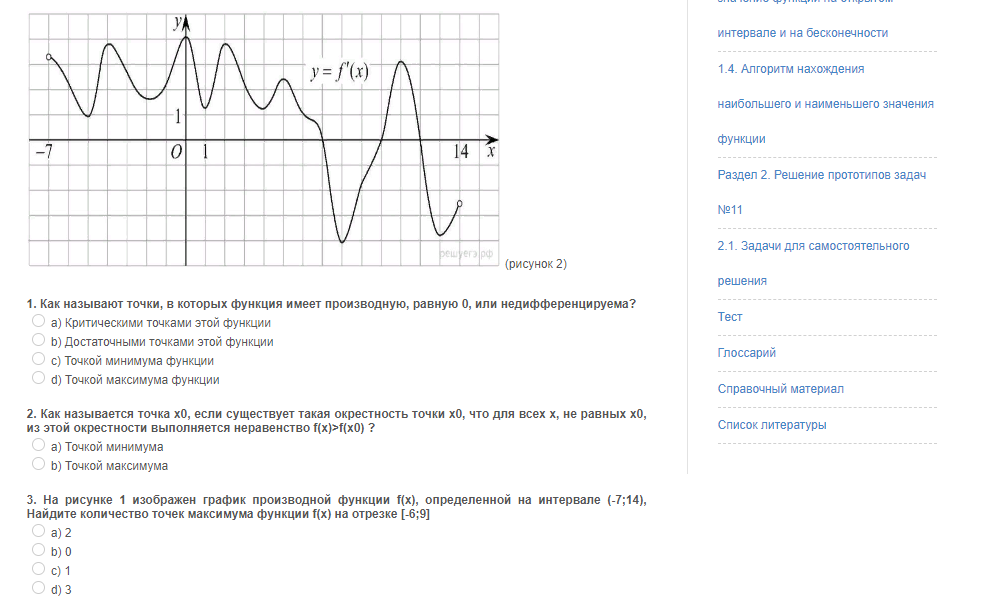
Рисунок 4. – Итоговое тестирование

Сами разделы содержат в себе теоретический материал по соответствующим методикам решения задач, примеры решения задач, а также типовые задачи для самостоятельного решения, которые могут быть использованы учителем на уроке математики, в конце учебника предусмотрен тест для закрепления всего изученного материала.

При разработке электронного образовательного издания были использованы: MSWord, Paint и TurboSite.

Заключение

Практическая зависимость данной курсовой работы заключается в возможности использования разработанного электронного учебника в рамках курса «Математика» и подготовке к профильному ЕГЭ для учащихся образовательных школ, которое можно использовать на уроке открытия новых знаний, закреплении материала, проверке знаний обучающихся, а также самостоятельного изучения данной темы школьниками.

Результатом проведенной работы стало достижение цели и создание учебного и многофункционального электронного образовательного издания на тему: «Решение задач №11 на нахождение наибольшего и наименьшего значения функции из ЕГЭ по математике», а также выполнение всех намеченных задач:

1. 
   Определено понятие «электронное образовательное издание», изучены и проанализированы его особенности и принципы построения;
   
2. 
   Проанализировано содержание учебников по математике в электронной форме, и определены структура и содержание ЭОИ;
   
3. 
   В соответствии с изученным материалом систематизированы и выражены в электронной форме методические материалы, учебные и контрольные задания;
   
4. 
   На основе отобранных материалов и технологий разработано электронное учебное издание по теме «Решение задач №11 на нахождение наибольшего и наименьшего значения функции из ЕГЭ по математике».
   

---

Данный учебник будет полезен как учителям, так и обучающимся для достижения следующих целей и задач:

Цели для педагога:

- Развитие математических, интеллектуальных способностей учащихся, обобщенных умственных умений;

- Создание условий для самореализации учащихся в процессе учебной деятельности;

Задачи для педагога:

- Помочь овладеть конкретными математическими знаниями, необходимыми для применения в практической деятельности;

- Способствовать общему развитию, развитию логического и образного мышления;

- Формировать у учащихся устойчивый интерес к математике;

- Развивать логические способности и качества мышления, характерные для математической деятельности;

- Подготовить к сознательному усвоению систематического курса математики;

- Раскрытие внутренних ресурсов личности ученика, выявление заложенных способностей.

Цели для учащихся: самостоятельно ознакомиться с применением производной для нахождения наибольшего и наименьшего значений функции.

Задачи для учащихся:

- Научиться решать задачи на нахождение наибольшего и наименьшего значения функции.

- Изучить способы решения популярных задач.

- Научиться решать задачи по алгоритму.

-Рассмотреть прикладные задачи на нахождение наибольшего и наименьшего значений.

---

Список литературы

1. 
   Актуальные проблемы развития среднего и высшего образования: межвуз. сб. науч. тр.– Челябинск: «Край Ра», 2017. – 180 с.
   
2. 
   Башмаков А.И., Башмаков И.А. Интеллектуальные информационные технологии. - М.: Изд - во МГТУ им. Н.Э. Баумана, 2009. - 304 с.
   
3. 
   Беленкова И.В. Технологии разработки современных электронных учебников и их использование в условиях ФГОС - Наука и перспективы, 2016. - 64-71с.
   
4. 
   Бужинская Н.В., Макаров И.Б. Обзор программных средств создания электронных учебников // Международный журнал экспериментального образования. - 2016. - №4-1. - С. 29-32.
   
5. 
   Бурдин Н. П. Гипертекстуальная структура как элемент электронного учебного издания // Научно-методический электронный журнал «Концепт». - 2016. - Т. 18. - С. 134-138.
   
6. 
   ГОСТ 7.83 - 2001. Система стандартов по информации, библиотечному и издательскому делу. Электронные издания. Основные виды и выходные сведения. Федеральное агентство по техническому регулированию и метрологии (протокол N20 от 2 ноября 2001 г.)
   
7. 
   Готская И.Б., Жучков В. М. Электронные образовательные ресурсы для новой школы // Universum: Вестник Герценовского университета. 2010.№1.С.76-79.
   
8. 
   Готская И.Б. Применение электронных образовательных ресурсов и дистанционных образовательных технологий для организации самостоятельной работы обучаюгцихся // Вестник Герценовского университета. - 2009. - № 6. - С. 30-32.
   
9. 
   Загвязинский В.И. Теория обучения. Современная интерпретация: учебное пособие для педагогических учебных заведений по специальности 031000 «Педагогика и психология», 033400 «Педагогика». - 2-е изд,, исправленное. - Москва: Академия, 2004. - 188с.
   
10. 
    Зимина О.В. Печатные и электронные учебные издания в
    

современном высшем образовании: Теория, методика, практика - М.: Изд-во МЭИ, - 2003. - 123 с.

11. 
    Зимина О.В. Печатные и электронные учебные издания в
    

современном высшем образовании: Теория, методика, практика. - 1 изд.- М.: МЭИ, 2008. - 267 с.

12. 
    Кравцова, А.Ю. Основные направления использования зарубежногоопыта развития методической системы подготовки учителей в область информационных и коммуникационных технологий(теорияипрактика)- М: Образование и информатика, 2003. - 232 с.
    
13. 
    КрасильниковаВ.А.Информационные и коммуникационные технологии в образовании: учебное пособие / В.А. Красильникова. - Оренбург: ГОУ ОГУ, 2006. - 235 с.
    
14. 
    Лапенок М.В. Информационная среда дистанционного обучения как средство развития классно-урочной системы в общеобразовательной школе, 2001. - 23 с.
    
15. 
    Лыскова В. Ю., Лысков А. М. Методические аспекты разработки электронных образовательных изданий и ресурсов // Вестник российских университетов. Математика. - 2009. - Т. 14. - №. 5-1.
    
16. 
    Мартиросян Л.П. Теоретико-методические основы информатизации математического образования : автореф. дис. докт.пед. наук- М., 2010. -42 с.
    
17. 
    Минин О.А. Электронные средства обучения в образовательном процессе: материалы лекции / О.А. Минин. - Репозиторий БГПУ. - 20 с.
    
18. 
    Рабинович П.Д., Баграмян Т.Э. К вопросу об инфраструктуре распределенного обучения / П.Д. Рабинович, Т.Э. Баграмян /7 Труды ПСА РАН, 2008. - Т. 8. - С. 205-228.
    
19. 
    Смокова Е.Ю. Внедрение электронных учебников в образовательный процесс // Территория науки. - 2017. - №2. - С. 69 - 74.
    
20. 
    Толковый словарь терминов понятийного аппарата информатизации образования / [сост.: И.В. Роберт, Т.А. Лавина]. - М: Институт Информатизации образования РАО, 2006. - 88 с.
    
21. 
    Шапиро, И.М. Использование задач с практическим содержанием в преподавании математики[Текст]: Книга для учителя./ И.М. Шапиро– М.: Просвещение, 1990. – 96 с
    
22. 
    Ященко, И.В. Методические указания для учителей, подготовленные на основе анализа типичных ошибок участников ЕГЭ 2019 года по математике. / И.В. Ященко, А.В. Семёнов, И.Р. Высоцкий. – М.: ФИПИ, 2019. – 45 с.
    

---

Приложение А

Глоссарий к электронному образовательному изданию на тему: «Решение задач №11 на нахождение наибольшего и наименьшего значения функции из ЕГЭ по математике»

Функция называется возрастающей на некотором промежутке, если большему значения аргумента из этого промежутка соответствует большее значение функции. То есть для любых двух значений из этого промежутка выполняется условие:

Функция называется убывающей на некотором промежутке, если большему значения аргумента из этого промежутка соответствует меньшее значение функции. То есть для любых двух значений из этого промежутка выполняется условие:

Наибольшее значение функции на некотором промежутке – это значение которое при любом значении делает справедливым неравенство

Наименьшее значение функции на некотором промежутке – это значение которое при любом значении делает справедливым неравенство

---