Файл: Экзаменационные вопросы по предмету тау.docx

Передаточная функция определяется только внутренними свойствами системы, является функцией комплексного переменного и обозначается



Передаточная функция характеризует динамику объекта по каналу, связывающему конкретный вход и выход объекта.



Рисунок - Примеры различных объектов: а) с одним входом и одним выходом; б) двумя входами и одним выходом; в) двумя входами и двумя выходами

Если объект имеет несколько входов и выходов, то он характеризуется несколькими передаточными функциями.

Передаточная функция характеризует динамику линейного объекта. Если задано дифференциальное уравнение, то для получения передаточной функции необходимо преобразовать дифференциальное уравнение по Лапласу и из алгебраического уравнения найти отношение   .

Дифференциальное уравнение объекта представляется в виде

a_ny⁽ⁿ⁾(t)+a_n−1y^(n–1)(t)+…+a₁y¢(t)+a₀y(t)=b_mx^(m)(t)+b_m−1x^(m-1)(t)+…+b₁x¢(t)+b₀x(t),

где a_n, …, a₀; b_m, …, b₀ – постоянные коэффициенты.

После преобразования по Лапласу при нулевых начальных условиях

a_nsⁿy(s)+a_n−1s^n–1y(s)+...+a₀y(s)=b_ms^mx(s)+b_m−1s^m–1x(s)+...+b₀x(s),

(a_nsⁿ+a_n−1s^n–1+...+a₁s+a₀)y(s)=(b_ms^m+b_m−1s^m–1+...+b₁s+b₀)x(s),

.

Если известна передаточная функция объекта, то изображение выхода объекта у(s)= W(s)x(s).

Передаточная функция является отношением полиномов

---

,

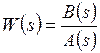
где B(s)=b_ms^m+b_m−lS^m–l+...+b₁s+b₀;

A(s)=a_nsⁿ+a_n−lS^n–l+…+a₁s+a₀y.

Для реальных физических объектов степень полинома В(s)всегда меньше или равна степени полинома A(s), то есть m ≤ n.

Для переходной функции входной сигнал x(t) = 1(t),   , выходной сигнал y(t) = h(t), y(s) = h(s), и тогда передаточная функция равна

.

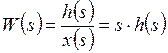Из этого выражения может быть получено выражение для переходной функции

.

Если известно выражение для весовой функции, то входной сигнал x(t) = δ(t), x(s) = 1, выходной сигнал w(t) и передаточная функция

,

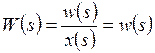является преобразованием Лапласа от весовой функции.

Из полученных выражений имеем w(s) = s×h(s), то есть w(t) = h¢(t).

14. 
    Временные характеристики САУ. Переходная, весовая функции.
    

Временной характеристикой системы называется закон изменения выходной величины в функции времени при изменении входного воздействия по определенному закону и при условии, что до приложения воздействия система находилась в покое. Временные характеристики определяются как реакция системы на типовые воздействия при нулевых начальных условиях.

К основным временным характеристикам относятся переходная функция и функция веса.

Типовые воздействия. В качестве типовых воздействий при исследовании систем используются:

– единичная функция;

– единичный импульс;

– линейно – растущее воздействие;

– квадратичное воздействие;

– гармоническое воздействие.

Переходная функция. Переходная функция h(t) – реакция системы на единичное воздействие при нулевых начальных условиях.

Весовая функция. Весовая функция k(t) – реакция системы на единичный импульс при нулевых начальных условиях.

Методы определения временных характеристик

1. Классический метод (основан на решении дифференциальных уравнений).

---

2. Операторный метод, использующий разложение на простые дроби.

3. Операторный метод, использующий вычеты.

4. Метод аналогового и цифрового моделирования.

5. Метод трапеций.

15. 
    Частотные характеристики САУ, в т.ч. логарифмические.
    

Частотными характеристиками называются зависимости, характеризующие реакцию звена на гармоническое входное воздействие в установившемся режиме, т.е. вынужденные синусоидальные колебания звена. Частотные характеристики, определяют зависимость между амплитудой и фазой входного и выходного гармонических сигналов при изменении частоты входного сигнала.

Если на вход линейного звена подать гармоническое воздействие:



где X₀ - амплитуда,

ω - угловая частота, имеющая размерность [рад/с] или [c-1],

то на выходе звена в установившемся режиме будет также гармоническая функция той же частоты, но другой амплитуды Y₀ и сдвинутая по фазе относительно входной величины на угол ψ:

 .

Связь между выходной гармоникой и входной устанавливается с помощью частотной передаточной функции звена W(jω).

Частотная передаточная функция представляет собой отношение изображений по Фурье выходного и входного сигналов при нулевых начальных условиях и равных нулю воздействиях на остальных входах:

 

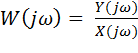
Из сравнения преобразований Фурье и Лапласа следует, что частотную передаточную функцию звена легко получить из его передаточной функции путем замены s на jω(подстановка Фурье), т.е.



Запись W( jω) означает, что в передаточную функцию W(s) подставляется чисто мнимое число s = jω , где j =   .

Зависимость отношения амплитуды выходного сигнала к амплитуде входного сигнала при фиксированной частоте называют 

---

амплитудной частотной характеристикой (сокращенно - АЧХ) и обозначают А(w).

Сдвиг фаз между входным и выходным сигналами при фиксированной частоте называют фазовой частотной характеристикой (ФЧХ) и обозначают j(w).

Амплитудная фазовая частотная характеристика (АФЧХ) строится на комплексной плоскости в полярных координатах и представляет собой геометрическое место концов векторов (годографов), соответствующих частотной передаточной функции W(jω) при изменении частоты от нуля до бесконечности.

Полученные точки соединяются затем плавной кривой. АФЧХ строится как для положительных, так и для отрицательных частот. При замене в W(jω) ω на -ω получается сопряженная комплексная величина. Поэтому АФЧХ для отрицательных частот является зеркальным отображением относительно вещественной оси АФЧХ для положительных частот.

Как видим, (АФЧХ) при ее определении в диапазоне частот от минус бесконечности до плюс бесконечности симметрична относительно оси абсцисс.

В ТАУ широко используются логарифмические частотные характеристики (ЛЧХ) : логарифмическая амплитудная ЧХ (ЛАЧХ) L( ) и логарифмическая фазовая ЧХ (ЛФЧХ)  ( ).

Они получаются путем логарифмирования передаточной функции:



ЛАЧХ получают из первого слагаемого, которое из соображений масштабирования умножается на 20, и используют не натуральный логарифм, а десятичный, то есть L( ) = 20lgA( ). Величина L( ) откладывается по оси ординат в децибелах. Изменение уровня сигнала на 10 дб соответствует изменению его мощности в 10 раз. Так как мощность гармонического сигнала Р пропорциональна квадрату его амплитуды А, то изменению сигнала в 10 раз соответствует изменение его уровня на 20дб,так как

---

lg(P₂/P₁) = lg(A₂²/A₁²) = 20lg(A₂/A₁).

По оси абсцисс откладывается частота w в логарифмическом масштабе. То есть единичным промежуткам по оси абсцисс соответствует изменение w в 10 раз. Такой интервал называется декадой. Так как lg(0) = -  , то ось ординат проводят произвольно.

ЛФЧХ, получаемая из второго слагаемого, отличается от ФЧХ только масштабом по оси  . Величина  ( ) откладывается по оси ординат в градусах или радианах. Для элементарных звеньев она не выходит за пределы: -       +  .

ЧХ являются исчерпывающими характеристиками системы. Зная ЧХ системы можно восстановить ее передаточную функцию и определить параметры.

16. 
    Пропорциональное звено. Диф. уравнение, передаточная функция, все временные и частотные характеристики. Примеры реализации.
    

---