Лабораторная работа №1
АНАЛИЗ ХАРАКТЕРИСТИК ЦИФРОВЫХ ФИЛЬТРОВ ДЛЯ ОБРАБОТКИ ОДНОМЕРНЫХ СИГНАЛОВ
по дисциплине «Цифровая обработка сигналов»


1. Цель работы: Изучение основ анализа характеристик цифровых фильтров.

Введение

Целью настоящей работы является изучение основ анализа характеристик цифровых фильтров.

Линейный цифровой фильтр (ЦФ) это устройство, в котором текущий отсчёт выходного сигнала представлен в виде линейной комбинации текущего отсчёта входного сигнала и предыдущих входных и выходных отсчётов. Обработка входных данных линейным ЦФ (без учёта эффектов квантования данных) описывается разностным уравнением



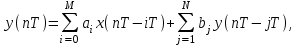
где x(nT) и y(nT) - отсчёты входного и выходного сигналов фильтра соответственно; 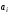и 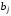- коэффициенты фильтра; M и N - целые числа, определяющие порядок фильтра; T- период дискретизации входных данных.

К основным характеристикам линейных ЦФ относятся: передаточная (системная) функция в Z - форме; импульсная и переходная характеристики; ампли­тудно-частотная и фазочастотная характеристики; точностные характеристики.

Передаточной функцией H(z) фильтра называют отношение Z - образа выходного сигнала Y(z) к Z - образу входного сигнала фильтра X(z) при нулевых начальных условиях, т.е. при y(-T) = y(-2T) = ... = y(-NT) = 0 и, кроме того, x(nT) = 0 при n < 0:

1. 
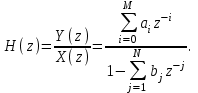
   Исследование параметров цифровых фильтров
   

На основе приведенных ниже передаточных функций (таб. 1.1) определим коэффициенты цифровых фильтров и, подставляя их в программные модули, получим ИХ, ПХ, АЧХ и ФЧХ. Структурные схемы исследуемых цифровых звеньев.

Таблица 1.1 – Передаточные функции исследуемых цифровых фильтров

Цифровой интегратор с ограниченным временем суммирования (М = 3; 4; 5;)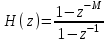
Цифровой дифференциатор (В1Р)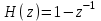
Вычислитель 2-й разности (В2Р)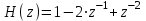
Всепропускающее звено (K = -0,8, ..., 0,8)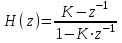
Сглаживающее звено (K = 0,3, ..., 0,9)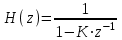

---

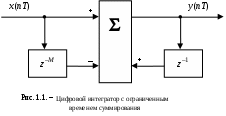
1) Цифровой интегратор с ограниченным временем суммирования (М=4)



Коэффициенты фильтра:


По полученным коэффициентам построим структурную схему фильтра (рис. 1.1).



Импульсная характеристика интегратора с ограниченным временем суммирования представлена на рис.1.2.



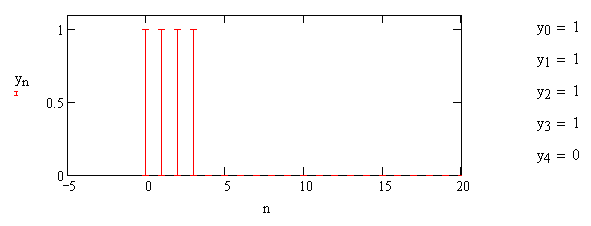
_{Рис. 1.2 – Импульсная характеристика интегратора с ограниченным временем суммирования}

Переходная характеристика интегратора с ограниченным временем суммирования представлена на рис.1.3.



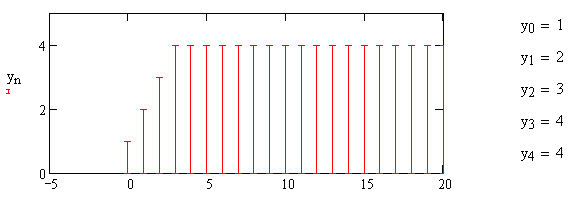
_{Рис. 1.3 – Переходная характеристика интегратора с ограниченным временем суммирования}

АЧХ интегратора с ограниченным временем суммирования представлена на рис.1.4.



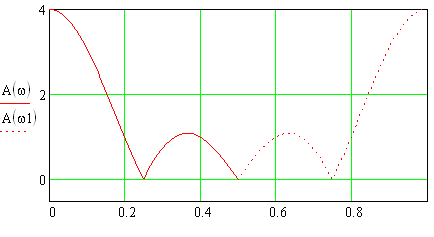
_{Рис. 1.4 – АЧХ интегратора с ограниченным временем суммирования}

ФЧХ интегратора с ограниченным временем суммирования представлена на рис.1.5.

---

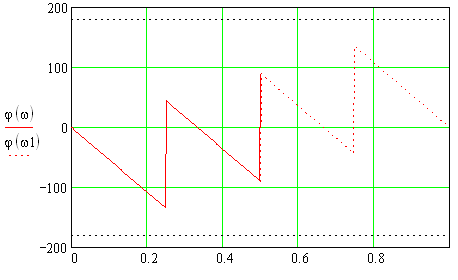
_{Рис. 1.5 – ФЧХ интегратора с ограниченным временем суммирования}
2) Цифровой дифференциатор (В1Р)



Коэффициенты фильтра:





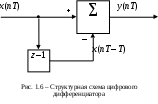
По полученным коэффициентам построим структурную схему фильтра (рис. 1.6).

Импульсная характеристика цифрового дифференциатора (В1Р) представлена на рис.1.7.



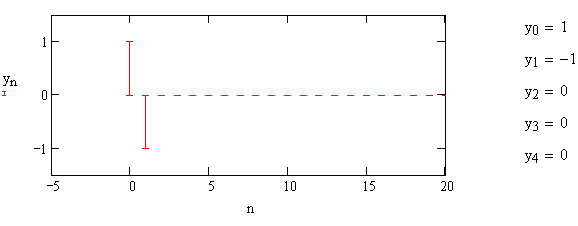
_{Рис. 1.7 – Импульсная характеристика цифрового дифференциатора (В1Р})

Переходная характеристика цифрового дифференциатора (В1Р) представлена на рис.1.8.



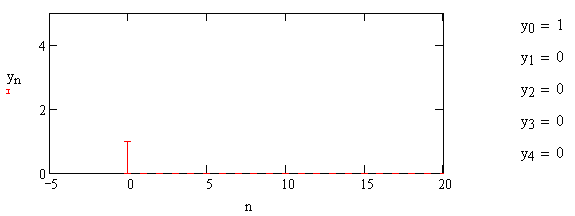
_{Рис. 1.8 – Переходная характеристика цифрового дифференциатора (В1Р)}

АЧХ цифрового дифференциатора (В1Р) представлена на рис.1.9.



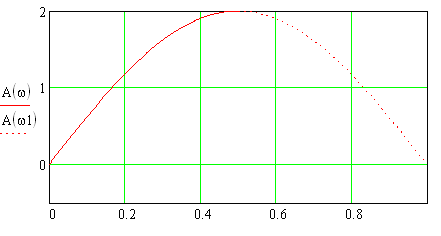
_{Рис. 1.9 – АЧХ цифрового дифференциатора (В1Р)}
ФЧХ цифрового дифференциатора (В1Р) представлена на рис.1.10.

---

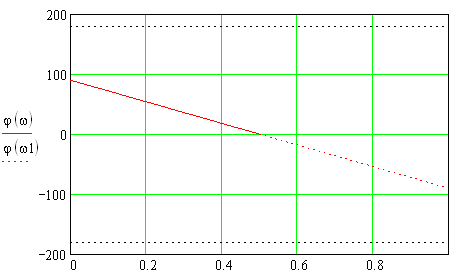
_{Рис. 1.10 – ФЧХ цифрового дифференциатора (В1Р)}
3) Вычислитель второй разности (В2Р)



_{Коэффициенты фильтра:}





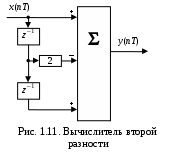
По полученным коэффициентам построим структурную схему фильтра (рис. 1.11).

Импульсная характеристика вычислителя второй разности (В2Р) представлена на рис.1.12.



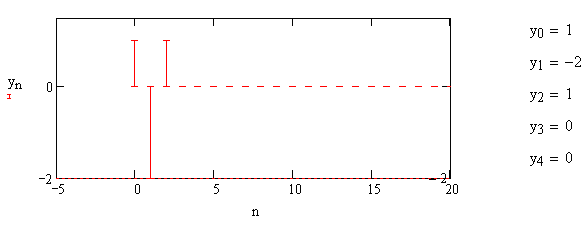
_{Рис. 1.12 – Импульсная характеристика вычислителя второй разности (В2Р)}

Переходная характеристика вычислителя второй разности (В2Р) представлена на рис.1.13.



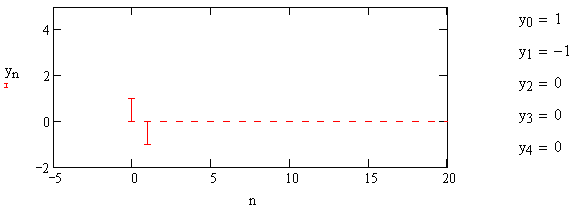
_{Рис. 1.13 – Переходная характеристика вычислителя второй разности (В2Р)}

АЧХ вычислителя второй разности (В2Р) представлена на рис.1.14.



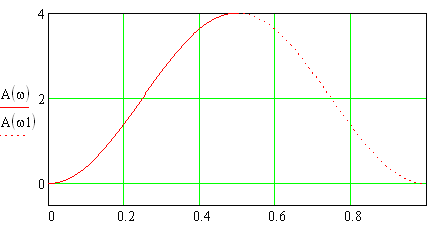
_{Рис. 1.14 – АЧХ вычислителя второй разности (В2Р)}

ФЧХ вычислителя второй разности (В2Р) представлена на рис.1.15.

---

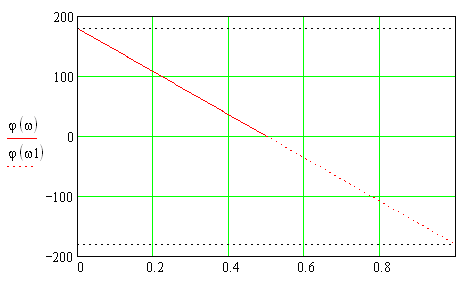
_{Рис. 1.15 – ФЧХ вычислителя второй разности (В2Р)}
4) Всепропускающее звено (K=0.3)



_{Коэффициенты фильтра:}


АЧХ всепропускающего звена представлена на рис.1.16.



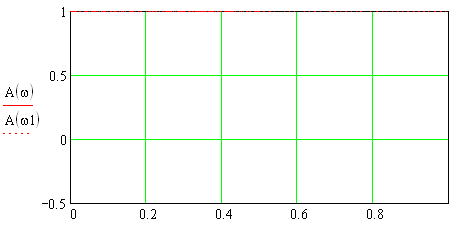
_{Рис. 1.16 – АЧХ всепропускающего звена}

Импульсная характеристика всепропускающего звена представлена на рис.1.17.



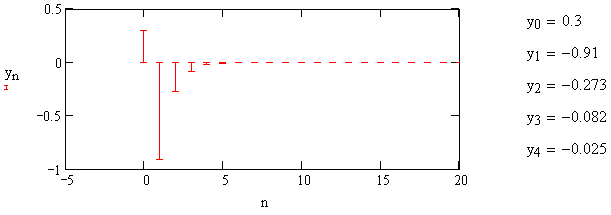
_{Рис. 1.17 – Импульсная характеристика всепропускающего звена}

Переходная характеристика всепропускающего звена представлена на рис.1.18.



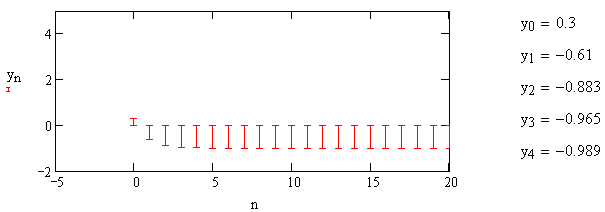
_{Рис. 1.18 – Переходная характеристика всепропускающего звена}

ФЧХ всепропускающего звена представлена на рис.1.19.

---

Смотрите также файлы

• Практическое задание 2, Модуль Общий план строения центральной нервной системы. Спинной мозг слушатель Федина Татьяна Андреевна Преподаватель Пузикова Ольга Юрьевна.docx

• Программа занятий специального педагога с Кулиевой Фахриёй 1 класс на 1 четверть 2022 2023 учебного года.docx

• 1. Как вы понимаете значение терминов объект управления исубъект управления.docx

• Реферат на тему Концепции и функции менеджмента.docx

• Как простой родник в белгородской глубинке превратился в святой источник.docx