Файл: Лабораторная работа 1 анализ характеристик цифровых фильтров для обработки одномерных сигналов по дисциплине Цифровая обработка сигналов.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 16.10.2024
Просмотров: 47
Скачиваний: 0
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
1 и b2.
Разностное уравнение без сохранения остатков :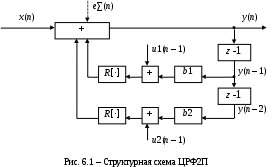
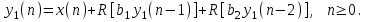
Разностное уравнение с сохранением остатков:
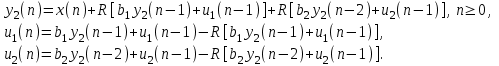
Дисперсия ошибки вычислений на выходе фильтра: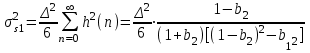 .
.
Дисперсия ошибки при сохранении остатков: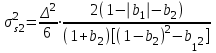
Эффективность метода при сохранении остатков можно определить с помощью отношения дисперсий:
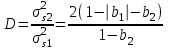 .
.
Графически дисперсии ошибок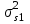 и
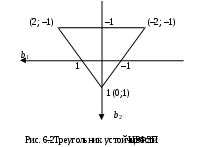
и 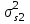 можно представить в виде полей на «треугольнике устойчивости» (рис. 6.2). Плоские части соответствуют усилению ошибок.
можно представить в виде полей на «треугольнике устойчивости» (рис. 6.2). Плоские части соответствуют усилению ошибок.
Двумерное поле ошибок округления в ЦФ второго порядка без учета остатков в зависимости от значений коэффициентов фильтрации В1 иВ2:
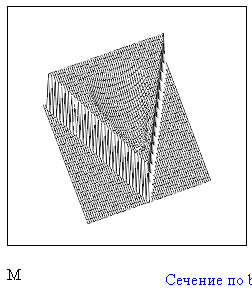
Рис.6.3 – Двумерное поле ошибок округления в ЦФ второго порядка без учета остатков в зависимости от значений коэффициентов фильтрации В1 иВ2.
Разрезы двумерного поля ошибок в зависимости от значений коэффициентов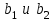 .
.
b1=0; b2=0
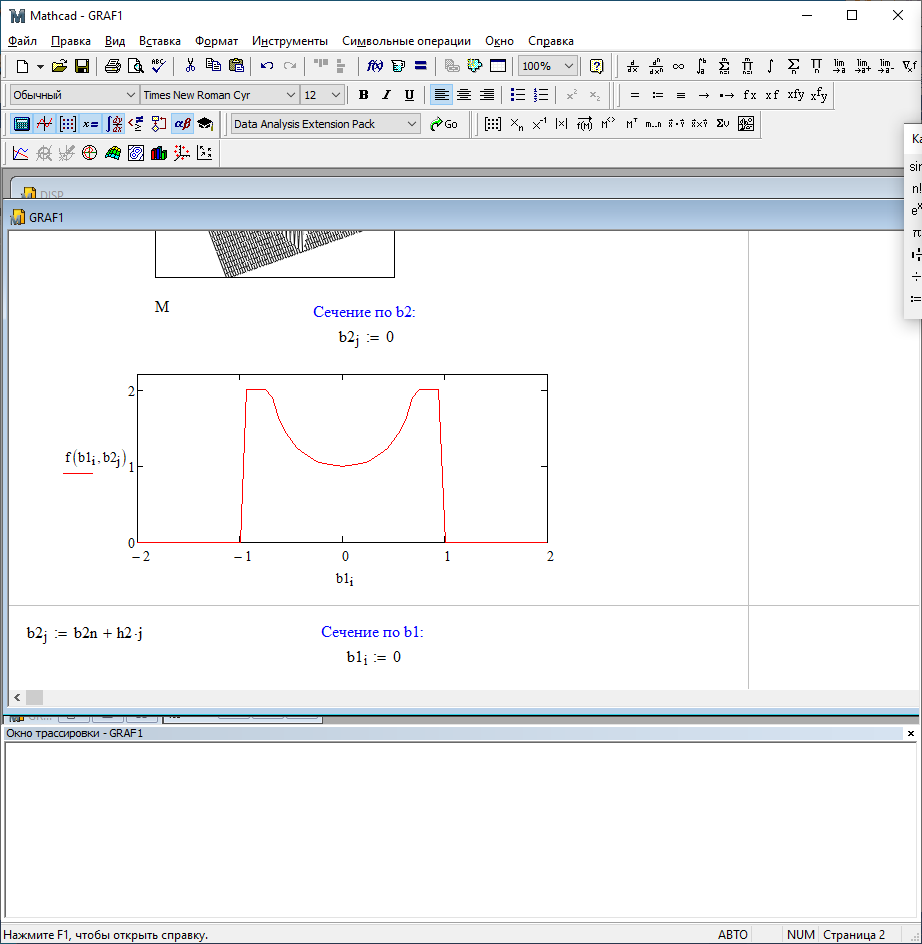
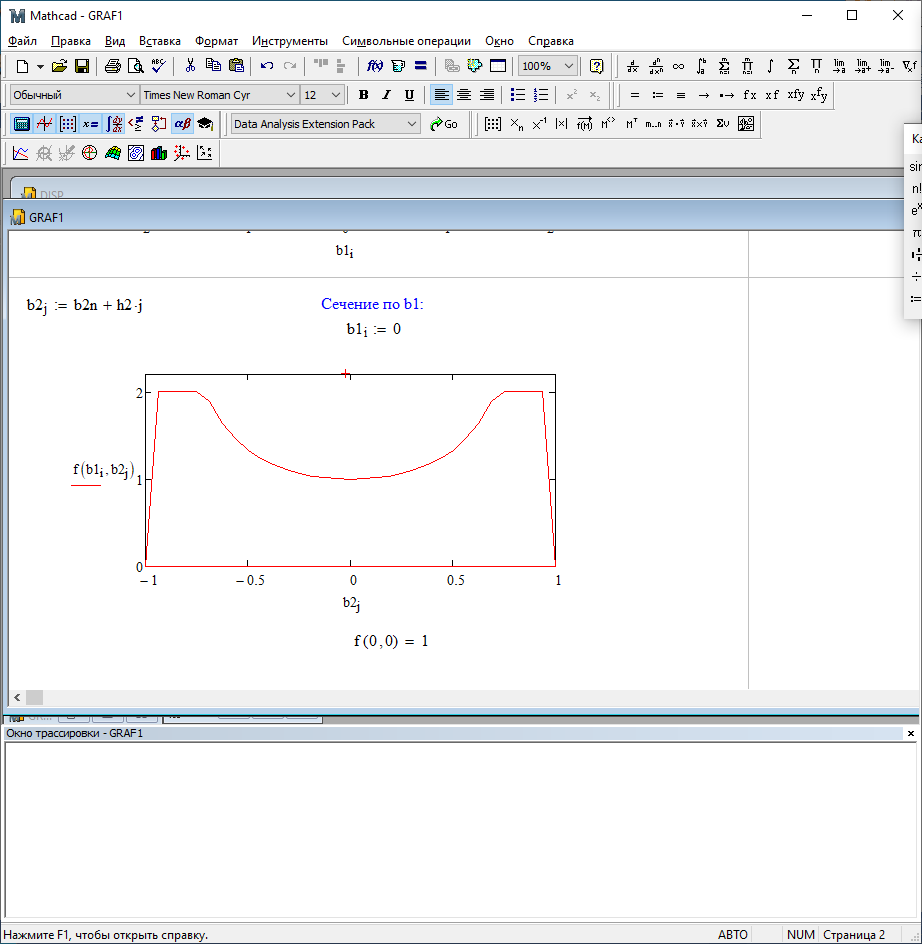
b1=0; b2=0,5
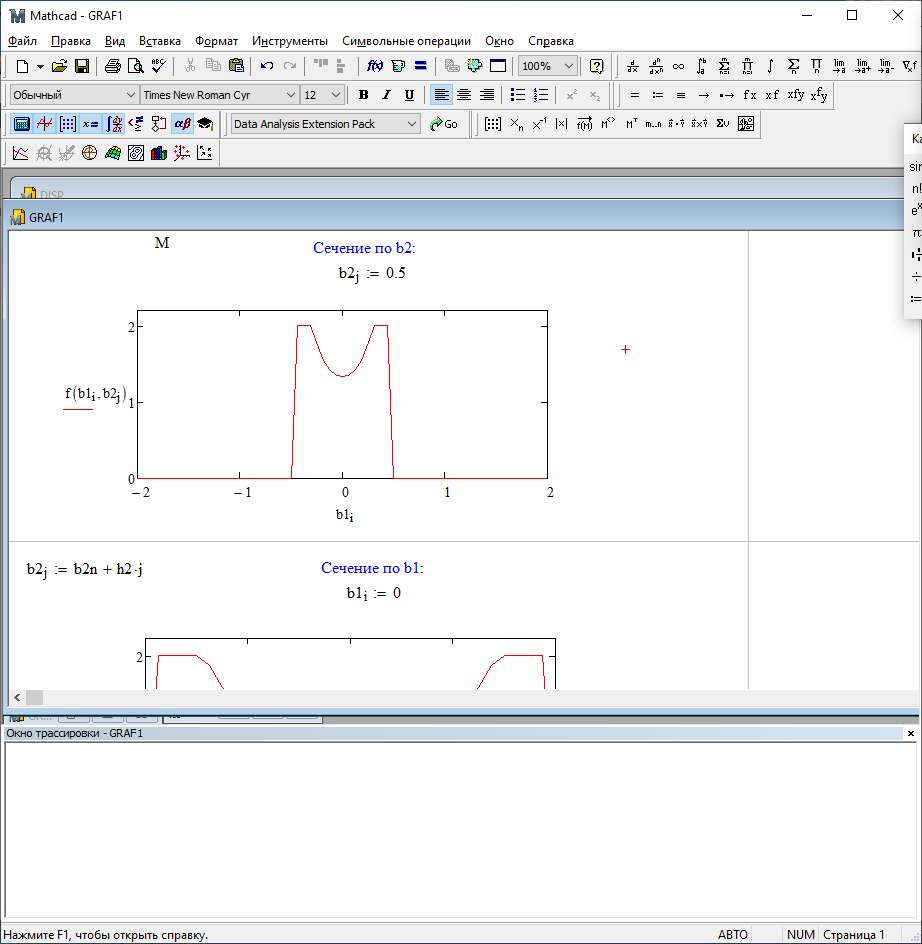
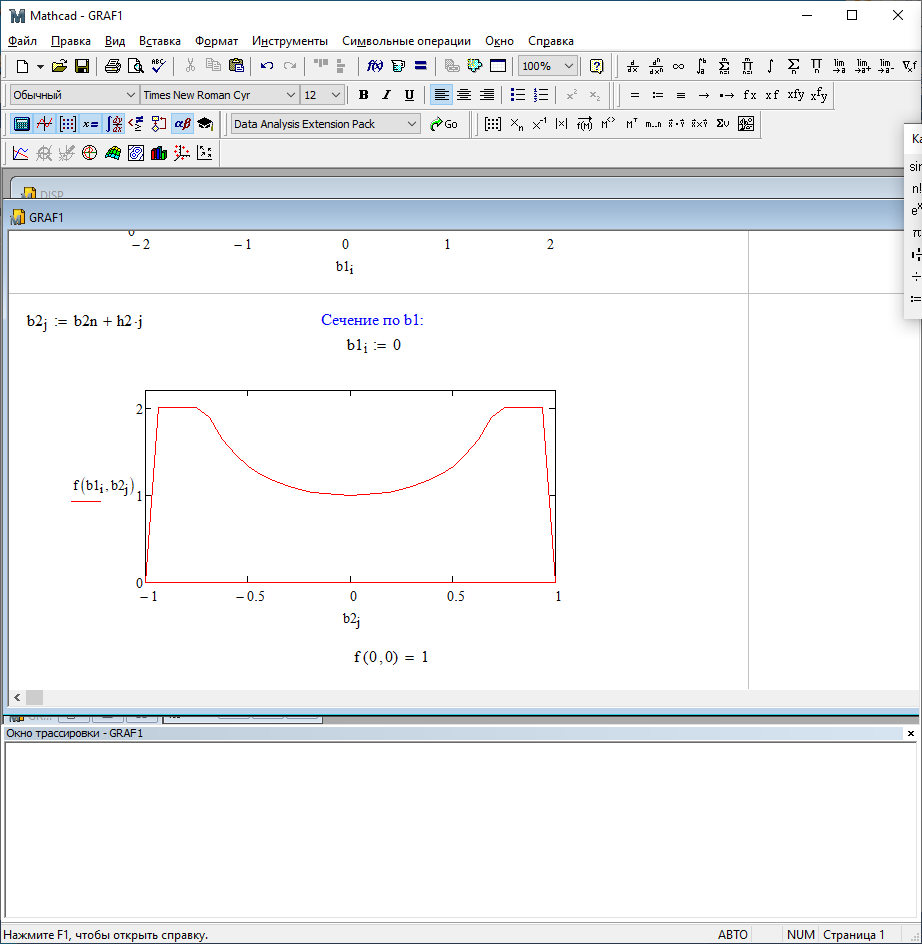
b1=0; b2=-0,5
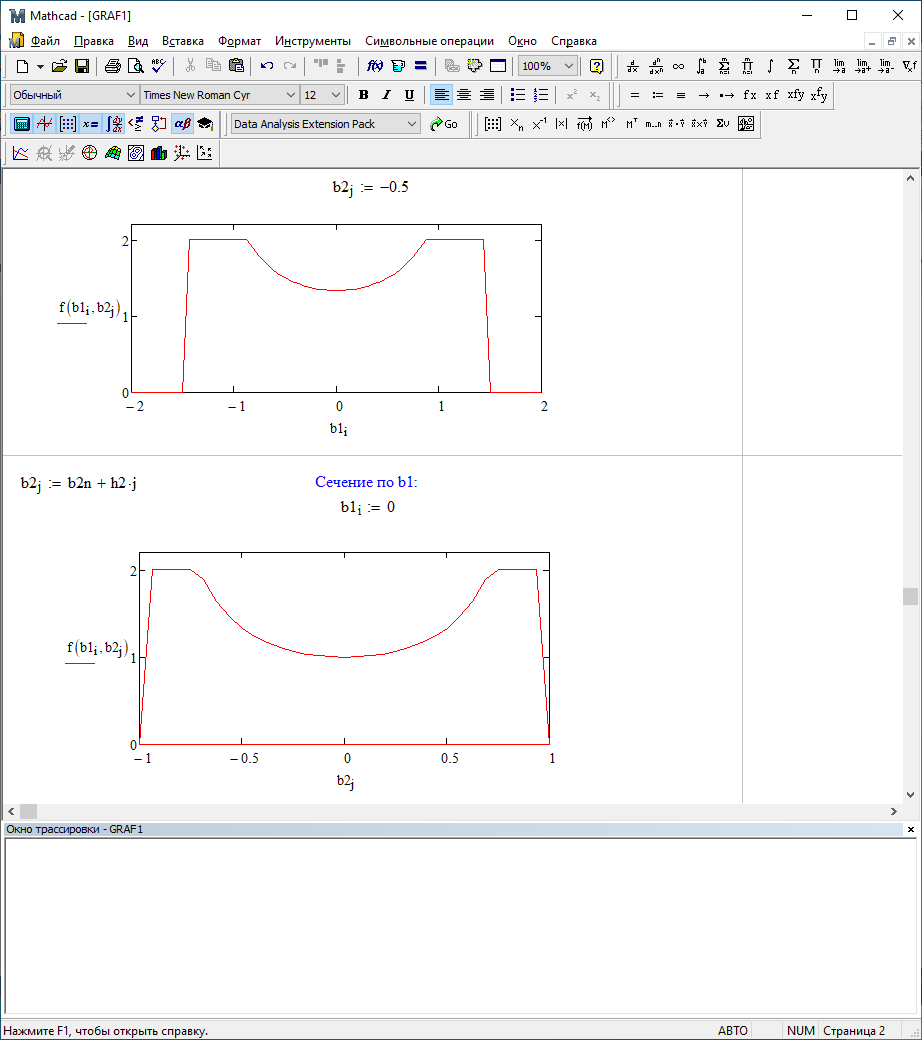

b1=0,5; b2=0
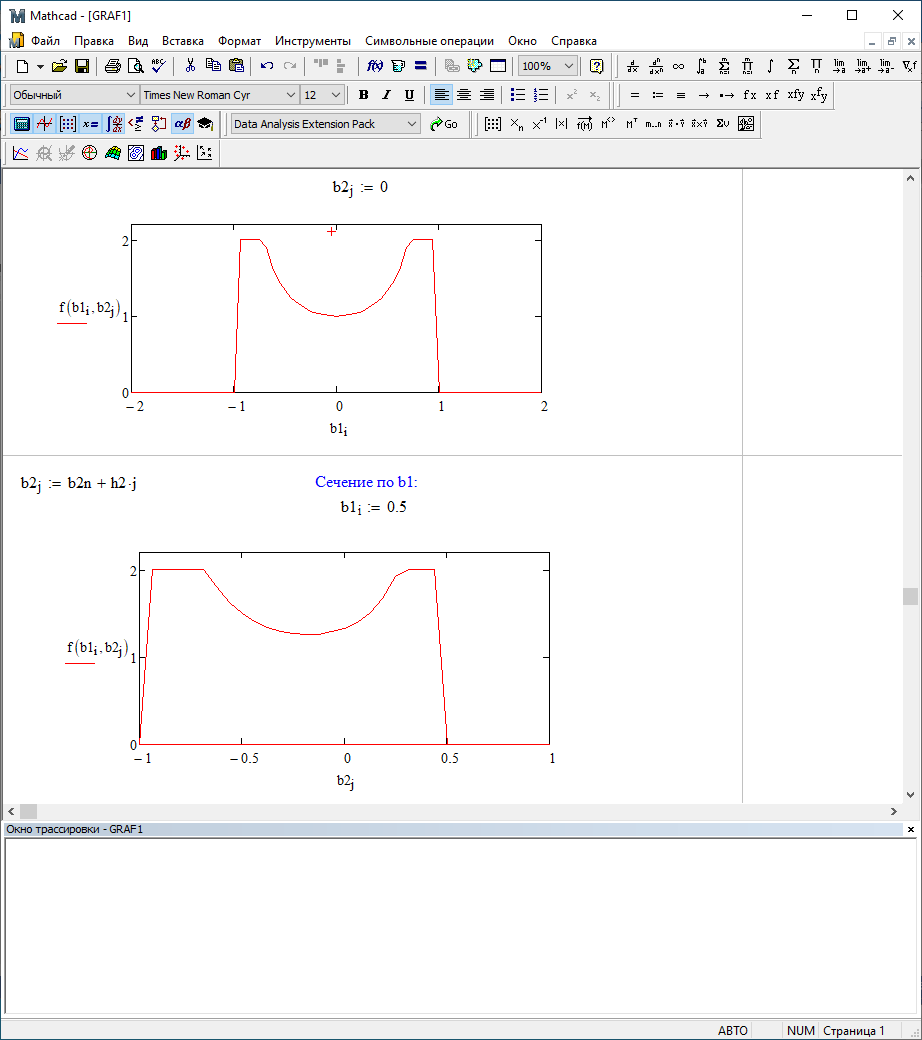

b1=-0,5; b2=0
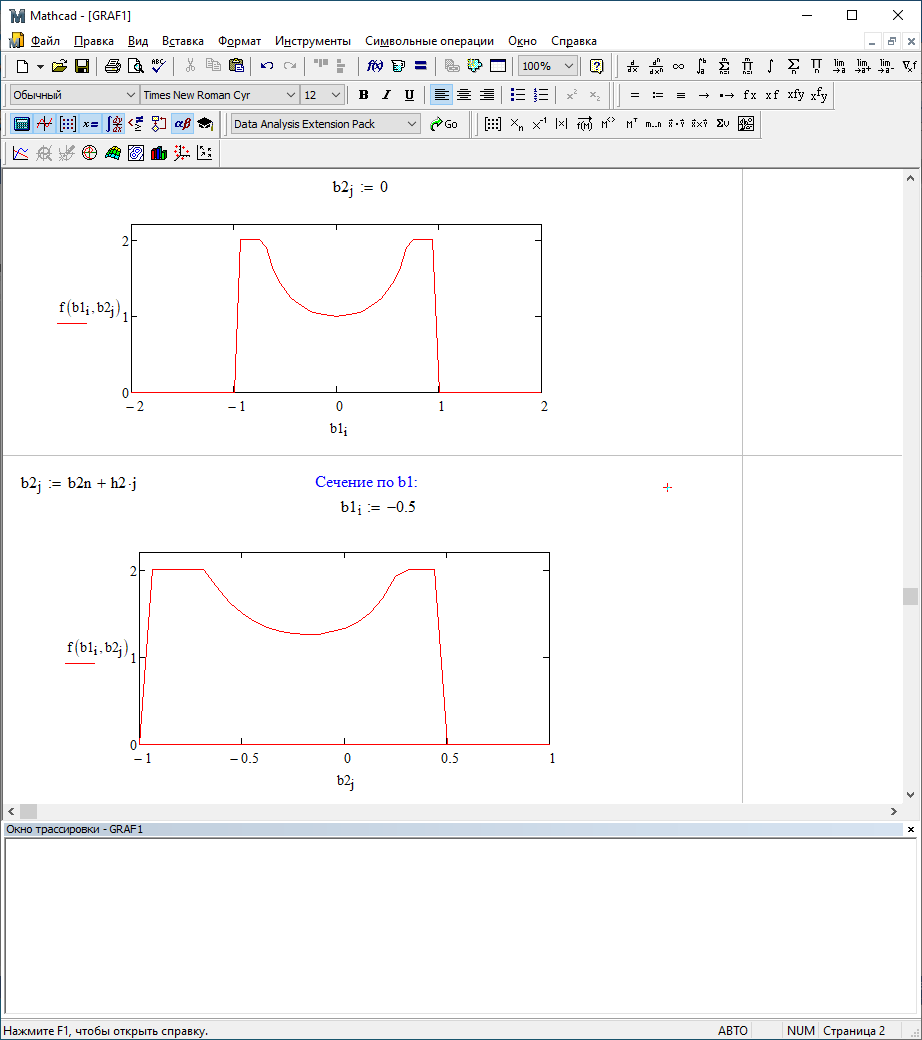

b1=0,9; b2=0,9
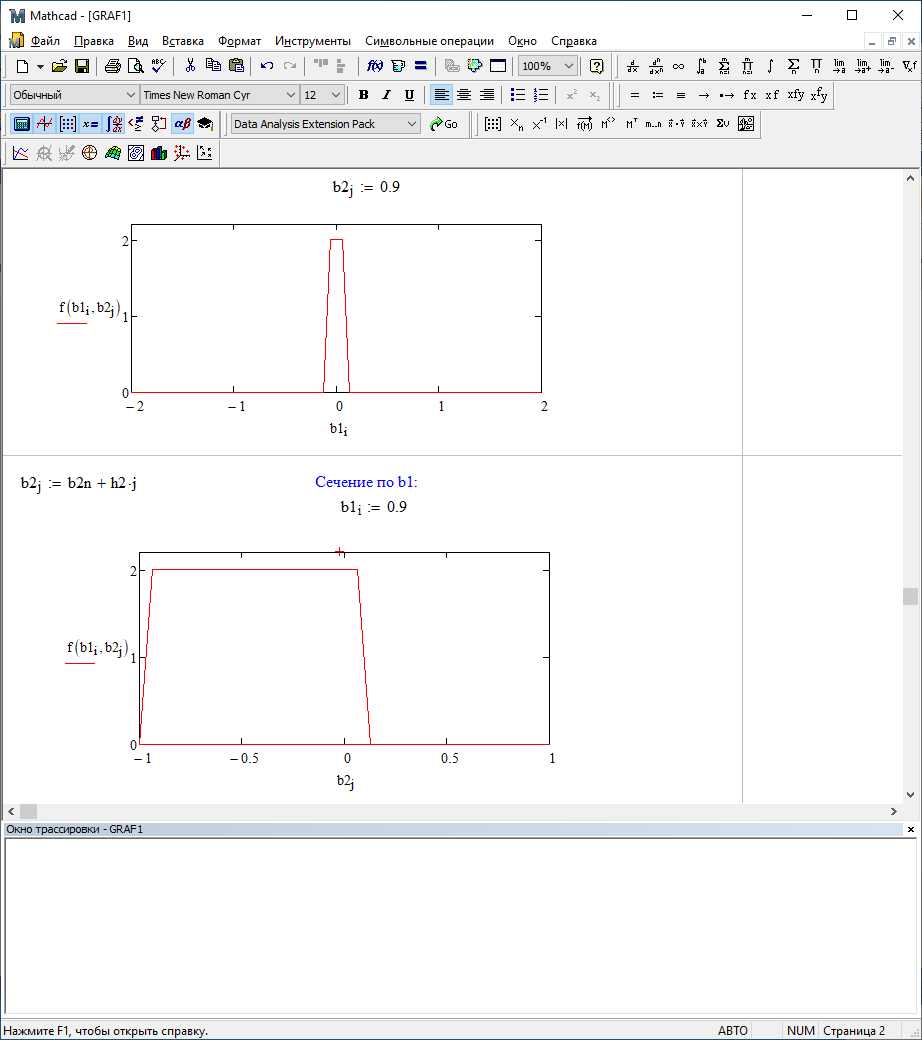

Двумерное поле ошибок округления в ЦФ второго порядка с учётом остатков в зависимости от значений коэффициентов фильтрации В1 иВ2:

Рис.6.4 – Двумерное поле ошибок округления в ЦФ второго порядка с учетом остатков в зависимости от значений коэффициентов фильтрации В1 и В2.
Разрезы двумерного поля ошибок в зависимости от значений коэффициентов .
.
b1=0; b2=0
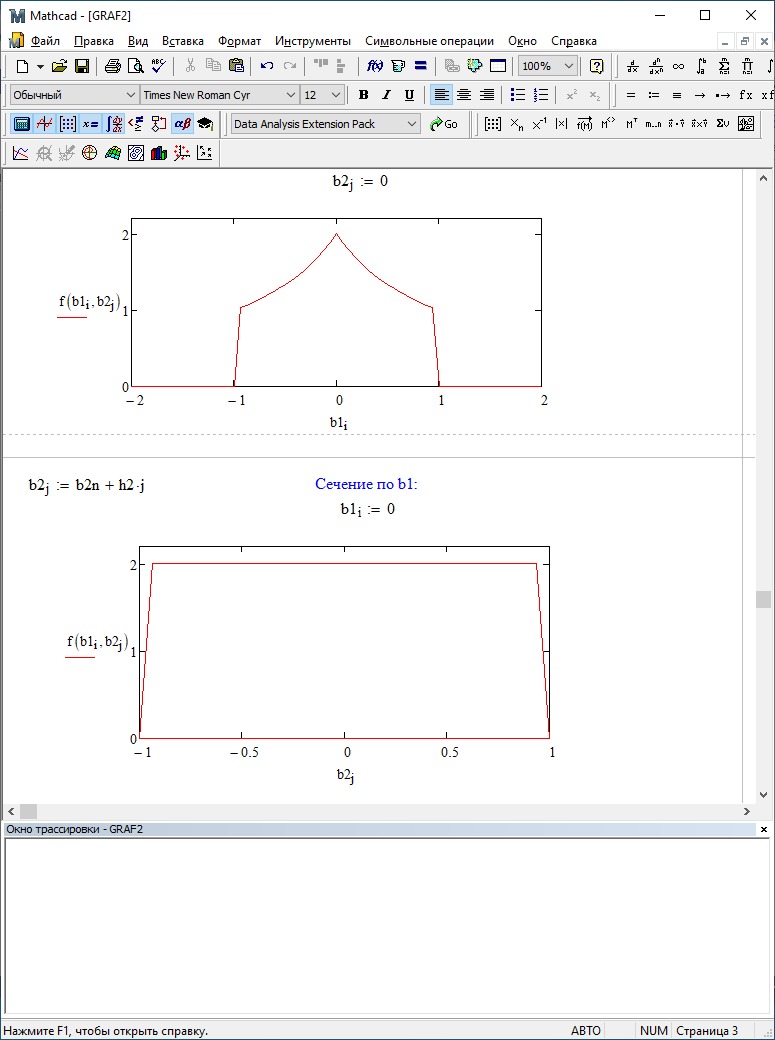

b1=0; b2=0,5
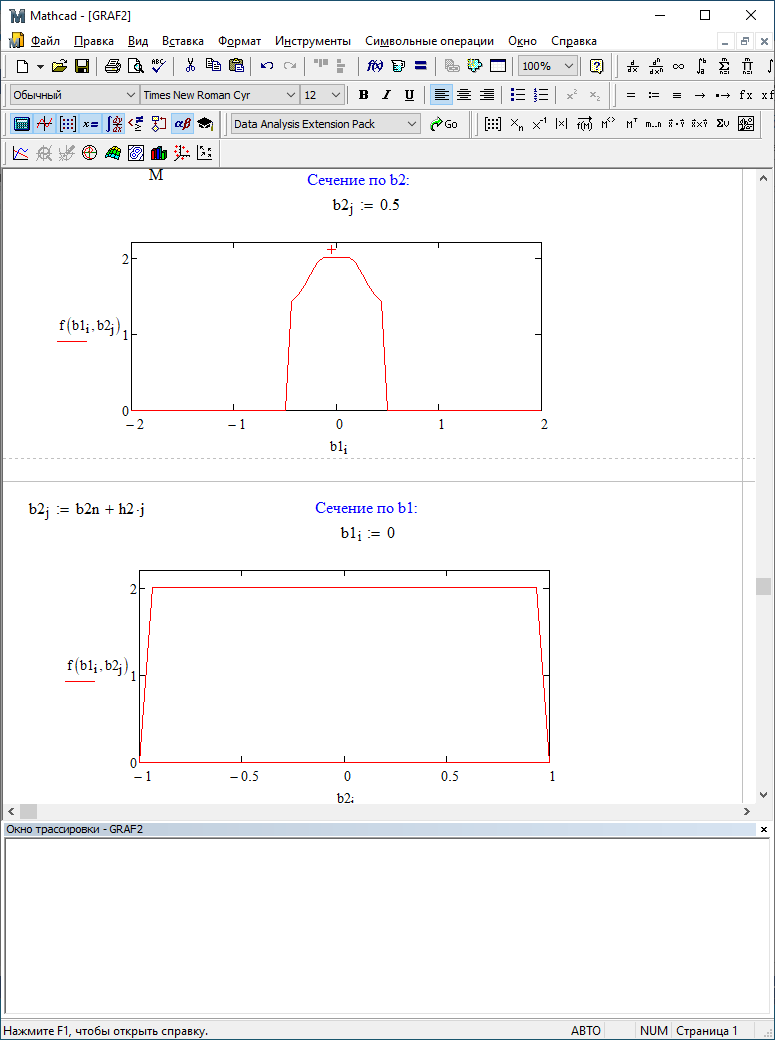

b1=0; b2=-0,5
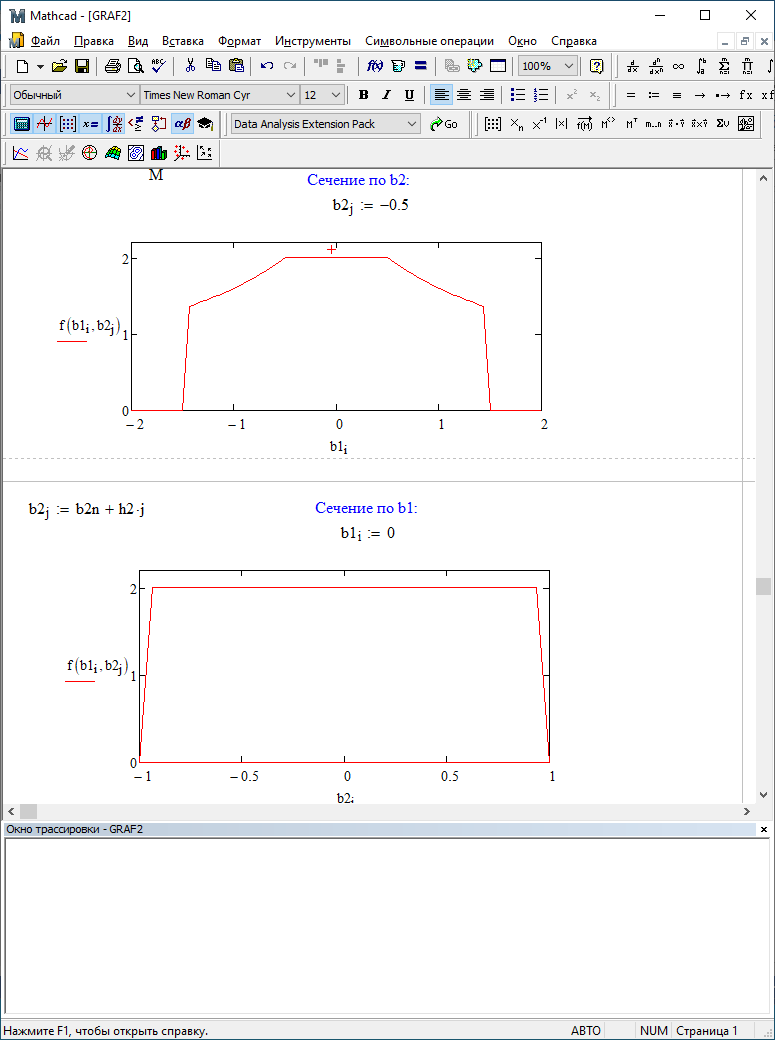

b1=0,5; b2=0
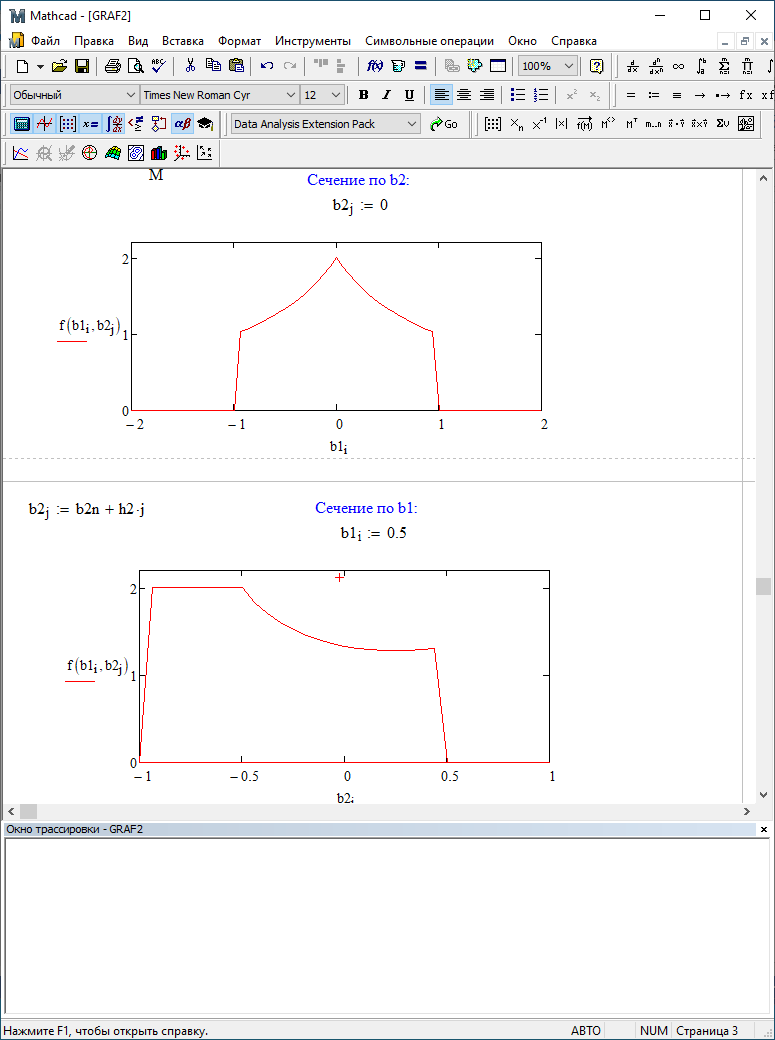

b1=-0,5; b2=0
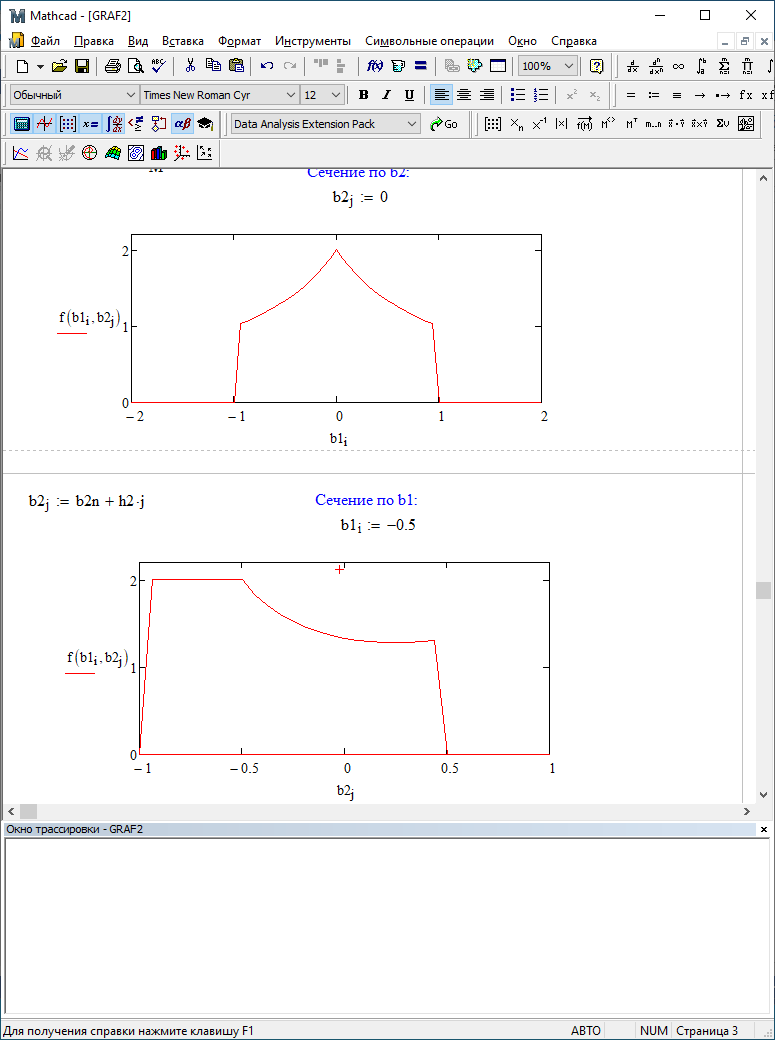

b1=0,9; b2=0,9

Двумерное поле относительной дисперсии ошибок для двух вариантов построения ЦФ второго порядка:

Рис.6.5 – Двумерное поле относительной дисперсии ошибок для двух вариантов построения ЦФ второго порядка.
Разрезы двумерного поля ошибок в зависимости от значений коэффициентов .
.
b1=0; b2=0
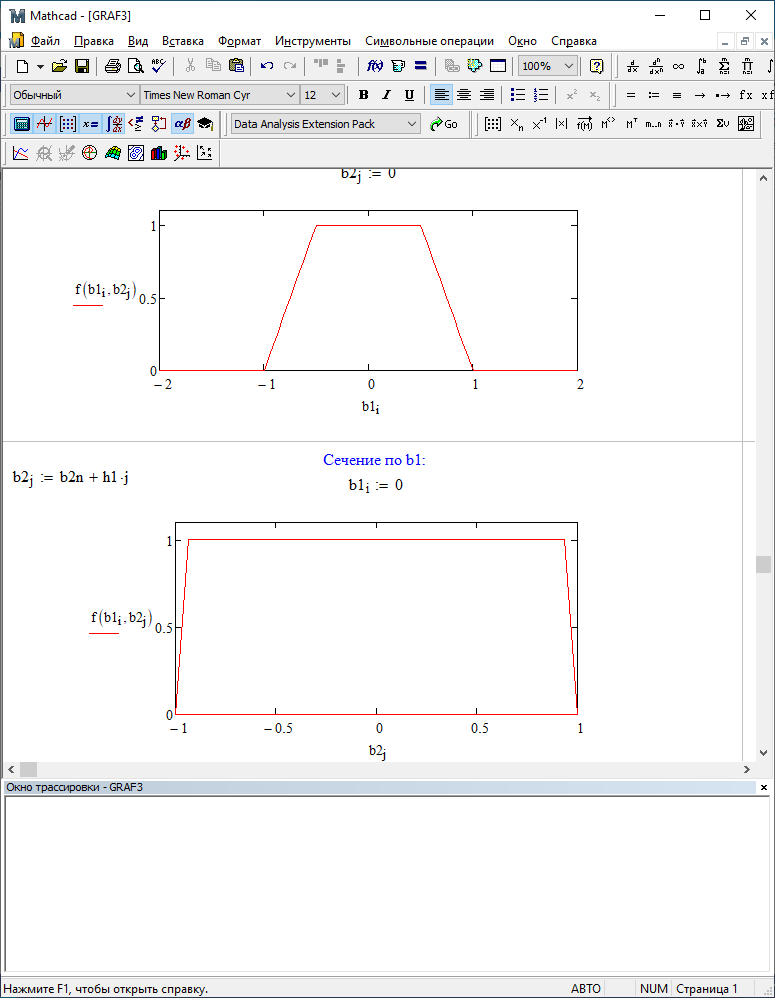

b1=0; b2=0,5
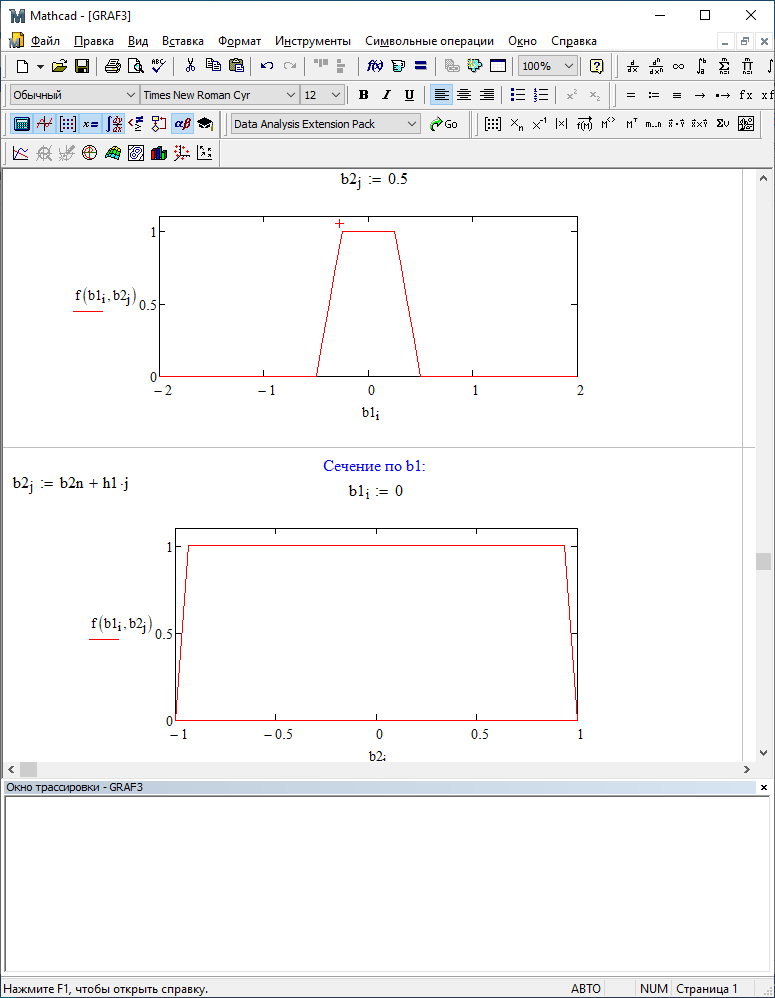

b1=0; b2=-0,5
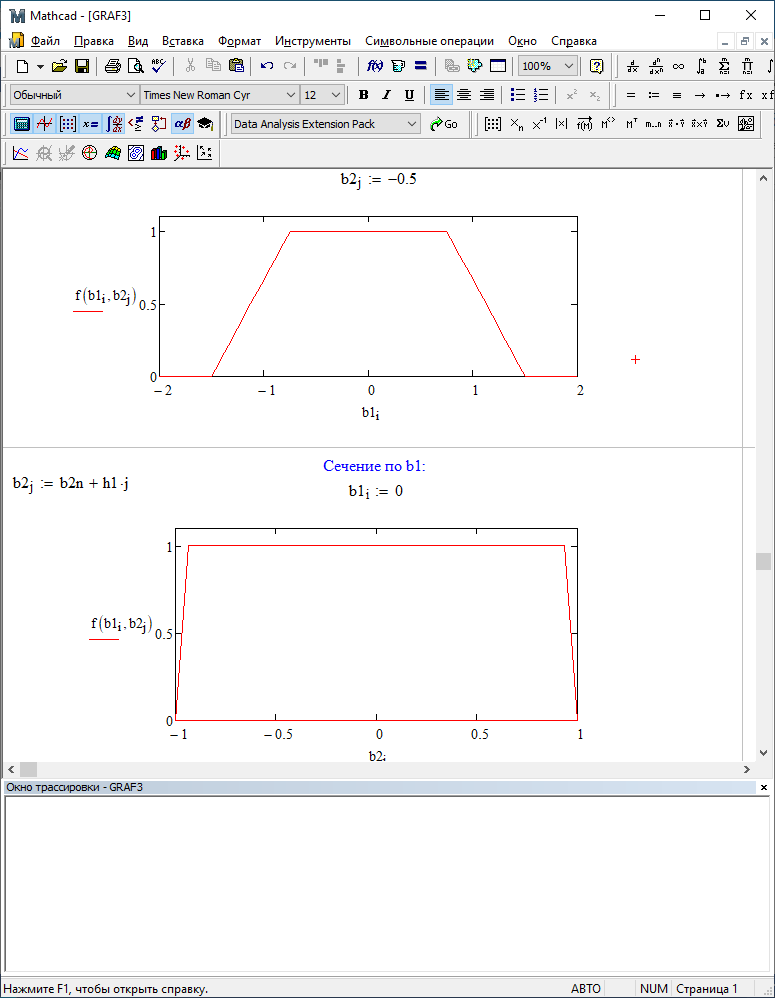

b1=0,5; b2=0
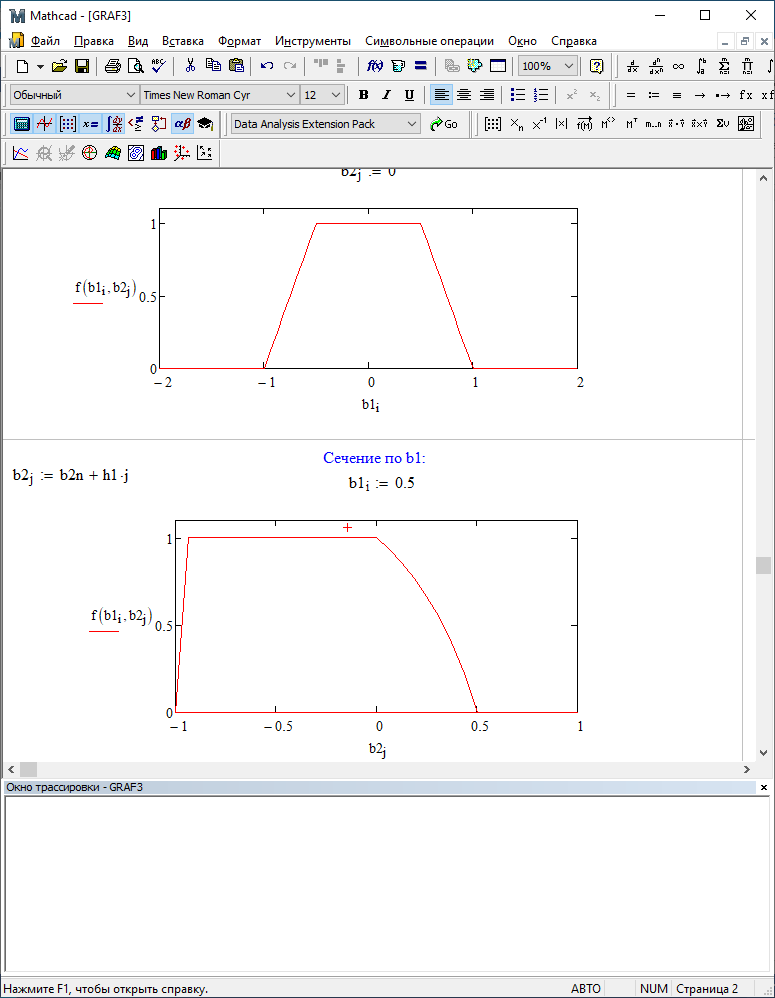

b1=-0,5; b2=0
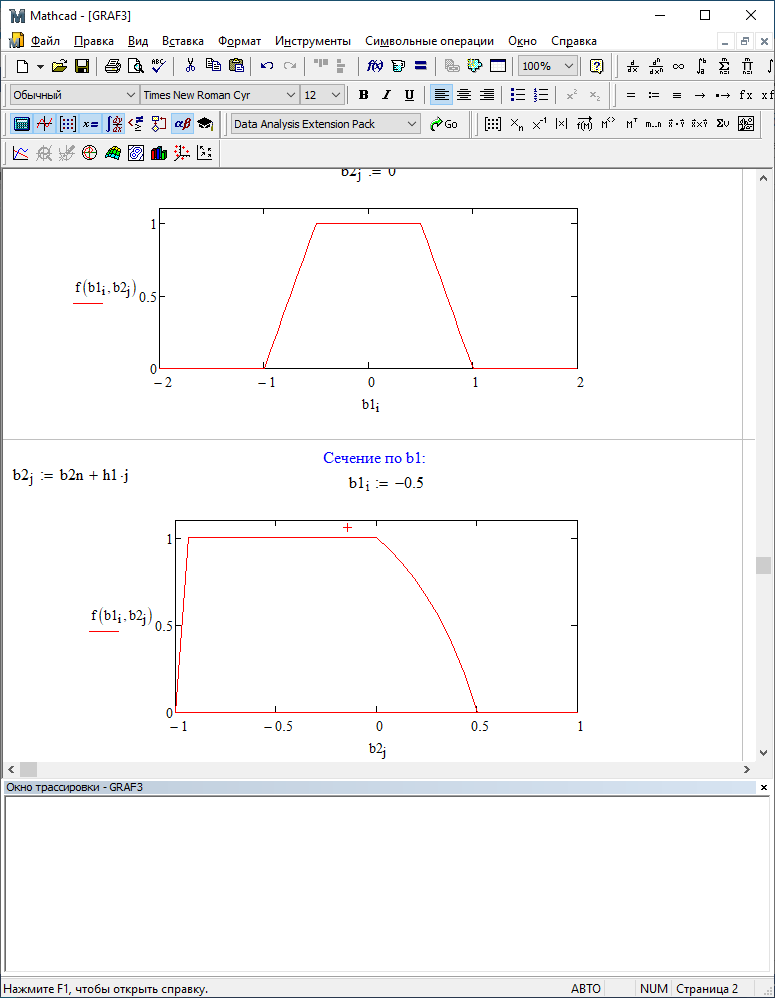

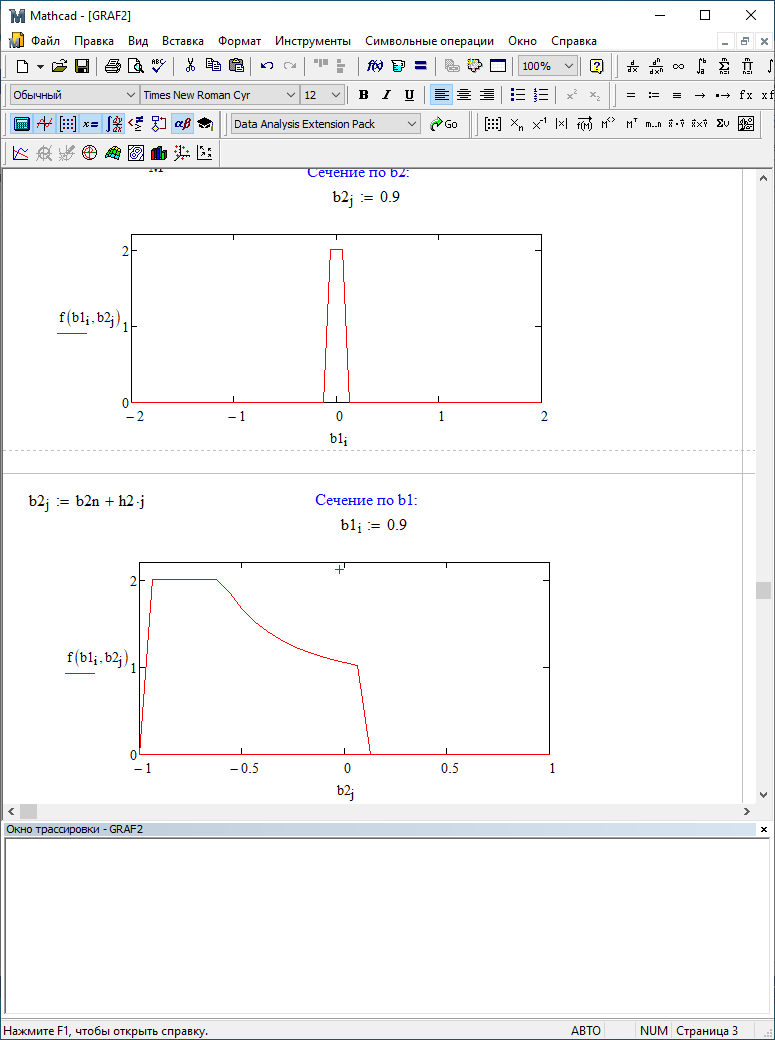
b1=0,9; b2=0,9
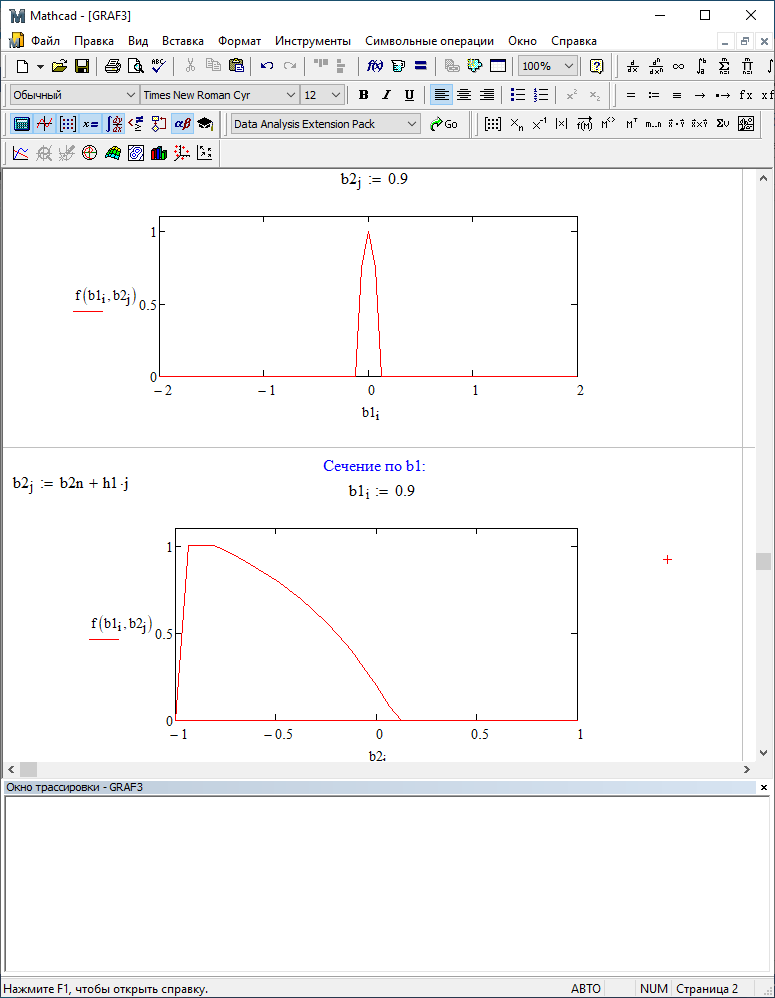

Таким образом, можно заметить, что выигрыш происходит на наклонных участках |b1| > 0,5. В этих областях предпочтительнее фильтр с использованием остатков, а на плоских областях лучше использовать фильтр без учета остатков.
7. Выводы
В данной лабораторной работе были построены ИХ и ПХ, АЧХ и ФЧХ для различных цифровых фильтров.
Полученные характеристики цифровых фильтров полностью соответствуют
характеристикам своих аналоговых фильтров-прототипов, что говорит о возможности применения ЦФ для фильтрации.
Также были построены вышеперечисленные характеристики для режекторного фильтра.
При уменьшении коэффициента b1 до 0,177 в ИХ и ПХ изменился только первый отсчет. Стал выше, вследствие того, что мы увеличили а0. АЧХ фильтра поднялась с 1 до 1.2 на нижних и верхних частотах (рис. 2.8). ФЧХ фильтра изменилась значительно. В области средних частот характеристика сильно исказилась. Появился «прогиб» характеристики вверх и вниз (рис. 2.9).
Было рассчитаны значения дисперсии. Можно сделать вывод о том, что значения, полученные экспериментальным путем, отличаются от теоретических с допустимой погрешностью.
Было рассмотрено двумерное поле ошибок округления в ЦФ второго порядка без учета остатков в зависимости от значений коэффициентов фильтрации В1 иВ2 При их увеличении происходит значительное уменьшение площади двумерного поля ошибок. Плоские части соответствуют усилению сшибок.
Для двумерного поля ошибок округления в ЦФ второго порядка с учётом остатков в зависимости от значений коэффициентов фильтрации В1 иВ2 видно также явное уменьшение площади поля ошибок, при увеличении b1 и b2. Явно выражено более грубое «урезание» сечения поля ошибок, по сравнению с полем ошибок без учета остатков.
Анализируя изменение поля отношения дисперсий от изменения коэффициентов, можно предположить, что выигрыш происходит на наклонных участках |b1| > 0,5. В этих областях предпочтительнее фильтр с использованием остатков, а на плоских областях лучше использовать фильтр без учета остатков.
Разностное уравнение без сохранения остатков :

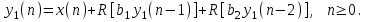
Разностное уравнение с сохранением остатков:
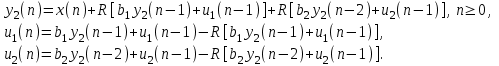
Дисперсия ошибки вычислений на выходе фильтра:
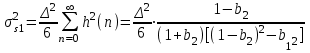 .
.Дисперсия ошибки при сохранении остатков:
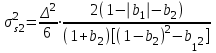
Эффективность метода при сохранении остатков можно определить с помощью отношения дисперсий:
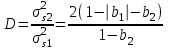 .
.Графически дисперсии ошибок
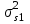 и
и 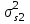 можно представить в виде полей на «треугольнике устойчивости» (рис. 6.2). Плоские части соответствуют усилению ошибок.
можно представить в виде полей на «треугольнике устойчивости» (рис. 6.2). Плоские части соответствуют усилению ошибок.
Двумерное поле ошибок округления в ЦФ второго порядка без учета остатков в зависимости от значений коэффициентов фильтрации В1 иВ2:

Рис.6.3 – Двумерное поле ошибок округления в ЦФ второго порядка без учета остатков в зависимости от значений коэффициентов фильтрации В1 иВ2.
Разрезы двумерного поля ошибок в зависимости от значений коэффициентов
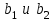 .
.b1=0; b2=0


b1=0; b2=0,5


b1=0; b2=-0,5


b1=0,5; b2=0


b1=-0,5; b2=0


b1=0,9; b2=0,9


Двумерное поле ошибок округления в ЦФ второго порядка с учётом остатков в зависимости от значений коэффициентов фильтрации В1 иВ2:

Рис.6.4 – Двумерное поле ошибок округления в ЦФ второго порядка с учетом остатков в зависимости от значений коэффициентов фильтрации В1 и В2.
Разрезы двумерного поля ошибок в зависимости от значений коэффициентов
 .
.b1=0; b2=0


b1=0; b2=0,5


b1=0; b2=-0,5


b1=0,5; b2=0


b1=-0,5; b2=0


b1=0,9; b2=0,9


Двумерное поле относительной дисперсии ошибок для двух вариантов построения ЦФ второго порядка:

Рис.6.5 – Двумерное поле относительной дисперсии ошибок для двух вариантов построения ЦФ второго порядка.
Разрезы двумерного поля ошибок в зависимости от значений коэффициентов
 .
.b1=0; b2=0


b1=0; b2=0,5


b1=0; b2=-0,5


b1=0,5; b2=0


b1=-0,5; b2=0


b1=0,9; b2=0,9


Таким образом, можно заметить, что выигрыш происходит на наклонных участках |b1| > 0,5. В этих областях предпочтительнее фильтр с использованием остатков, а на плоских областях лучше использовать фильтр без учета остатков.
7. Выводы
В данной лабораторной работе были построены ИХ и ПХ, АЧХ и ФЧХ для различных цифровых фильтров.
Полученные характеристики цифровых фильтров полностью соответствуют
характеристикам своих аналоговых фильтров-прототипов, что говорит о возможности применения ЦФ для фильтрации.
Также были построены вышеперечисленные характеристики для режекторного фильтра.
При уменьшении коэффициента b1 до 0,177 в ИХ и ПХ изменился только первый отсчет. Стал выше, вследствие того, что мы увеличили а0. АЧХ фильтра поднялась с 1 до 1.2 на нижних и верхних частотах (рис. 2.8). ФЧХ фильтра изменилась значительно. В области средних частот характеристика сильно исказилась. Появился «прогиб» характеристики вверх и вниз (рис. 2.9).
Было рассчитаны значения дисперсии. Можно сделать вывод о том, что значения, полученные экспериментальным путем, отличаются от теоретических с допустимой погрешностью.
Было рассмотрено двумерное поле ошибок округления в ЦФ второго порядка без учета остатков в зависимости от значений коэффициентов фильтрации В1 иВ2 При их увеличении происходит значительное уменьшение площади двумерного поля ошибок. Плоские части соответствуют усилению сшибок.
Для двумерного поля ошибок округления в ЦФ второго порядка с учётом остатков в зависимости от значений коэффициентов фильтрации В1 иВ2 видно также явное уменьшение площади поля ошибок, при увеличении b1 и b2. Явно выражено более грубое «урезание» сечения поля ошибок, по сравнению с полем ошибок без учета остатков.
Анализируя изменение поля отношения дисперсий от изменения коэффициентов, можно предположить, что выигрыш происходит на наклонных участках |b1| > 0,5. В этих областях предпочтительнее фильтр с использованием остатков, а на плоских областях лучше использовать фильтр без учета остатков.
