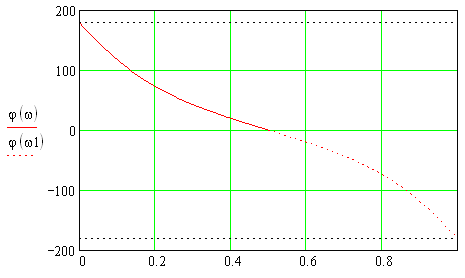
_{Рис. 1.19 – ФЧХ всепропускающего звена}

По полученным коэффициентам построим структурную схему фильтра (рис. 1.20).






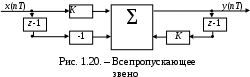
5) Сглаживающее звено (К=0,5)


_{Коэффициенты фильтра:}


АЧХ сглаживающего звена представлена на рис.1.21.



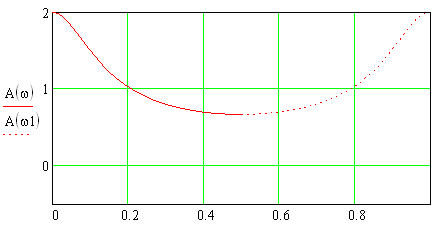
_{Рис. 1.21 – АЧХ сглаживающего звена}

Импульсная характеристика сглаживающего звена представлена на рис.1.22.



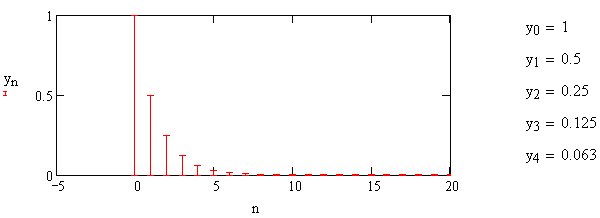
_{Рис. 1.22 – Импульсная характеристика сглаживающего звена}

Переходная характеристика сглаживающего звена представлена на рис.1.23.



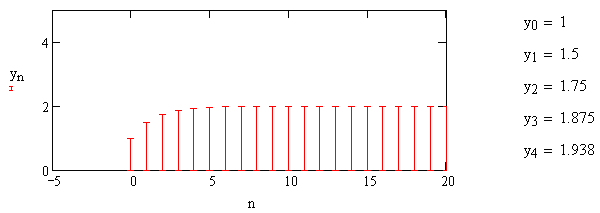
_{Рис. 1.23 – Переходная характеристика сглаживающего звена}

ФЧХ сглаживающего звена представлена на рис.1.24.

---

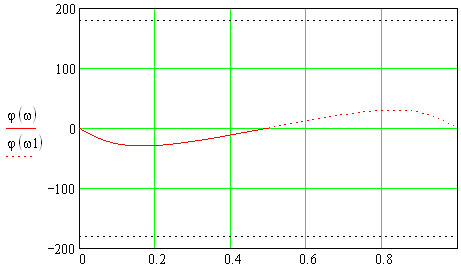
_{Рис. 1.24 – ФЧХ сглаживающего звена}
По полученным коэффициентам построим структурную схему фильтра (рис. 1.25).




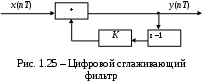
2. На основе варианта №5 получить АЧХ, ФЧХ, ИХ и ПХ. Опишите особенности характеристик исследованного фильтра. Изменяя один из коэффициентов в рекурсивной или нерекурсивной частях ЦФ опишите изменения, произошедшие с характеристиками фильтра. Объясните эти изменения. Приведите структурную схему фильтра.

Режекторный фильтр— фильтр с двумя полосами пропускания (от 0 до ω_сн и от ω_св до ∞) и одной полосой подавления.
Системная функция режекторного фильтра:


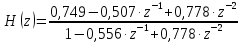
АЧХ и ФЧХ фильтра:

Используя программный модуль h(jw) получим следующие АЧХ и ФЧХ фильтра:



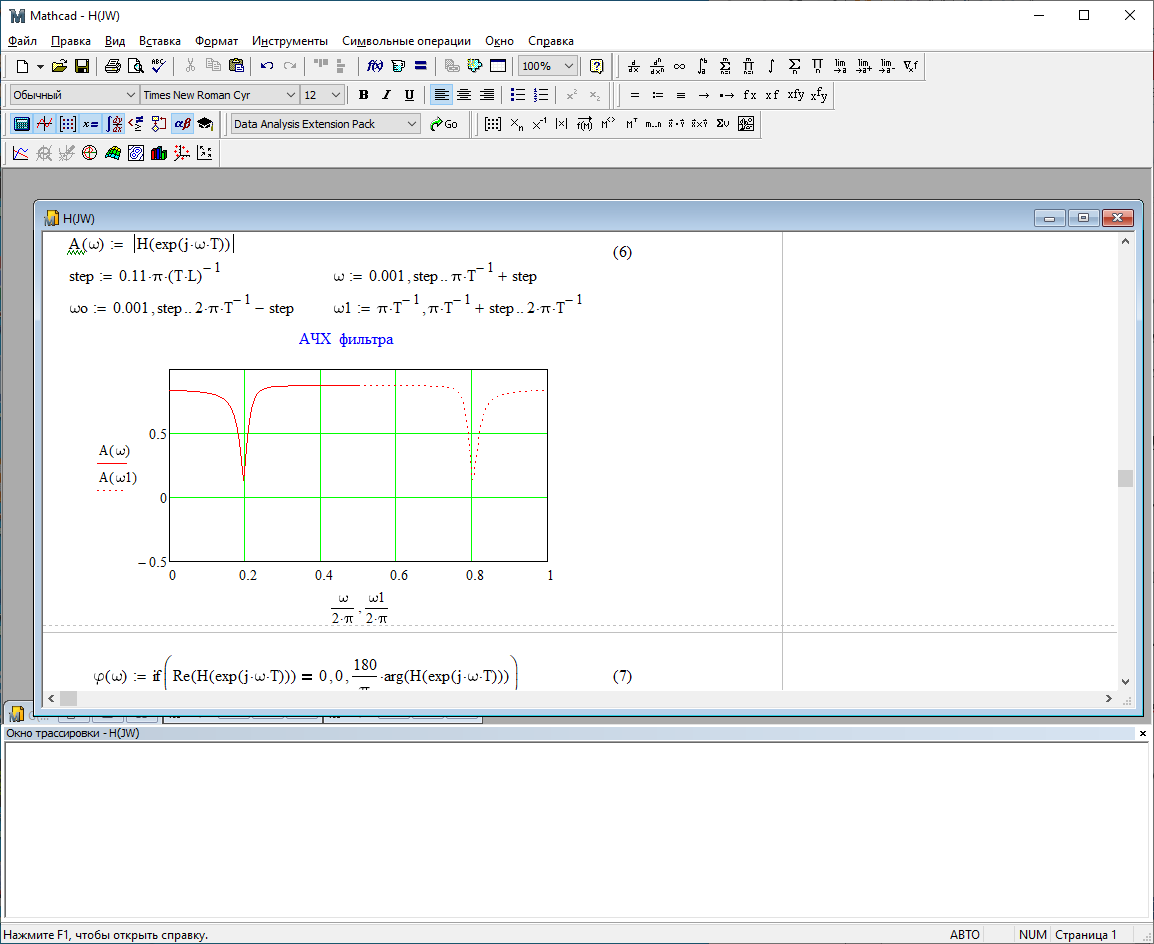
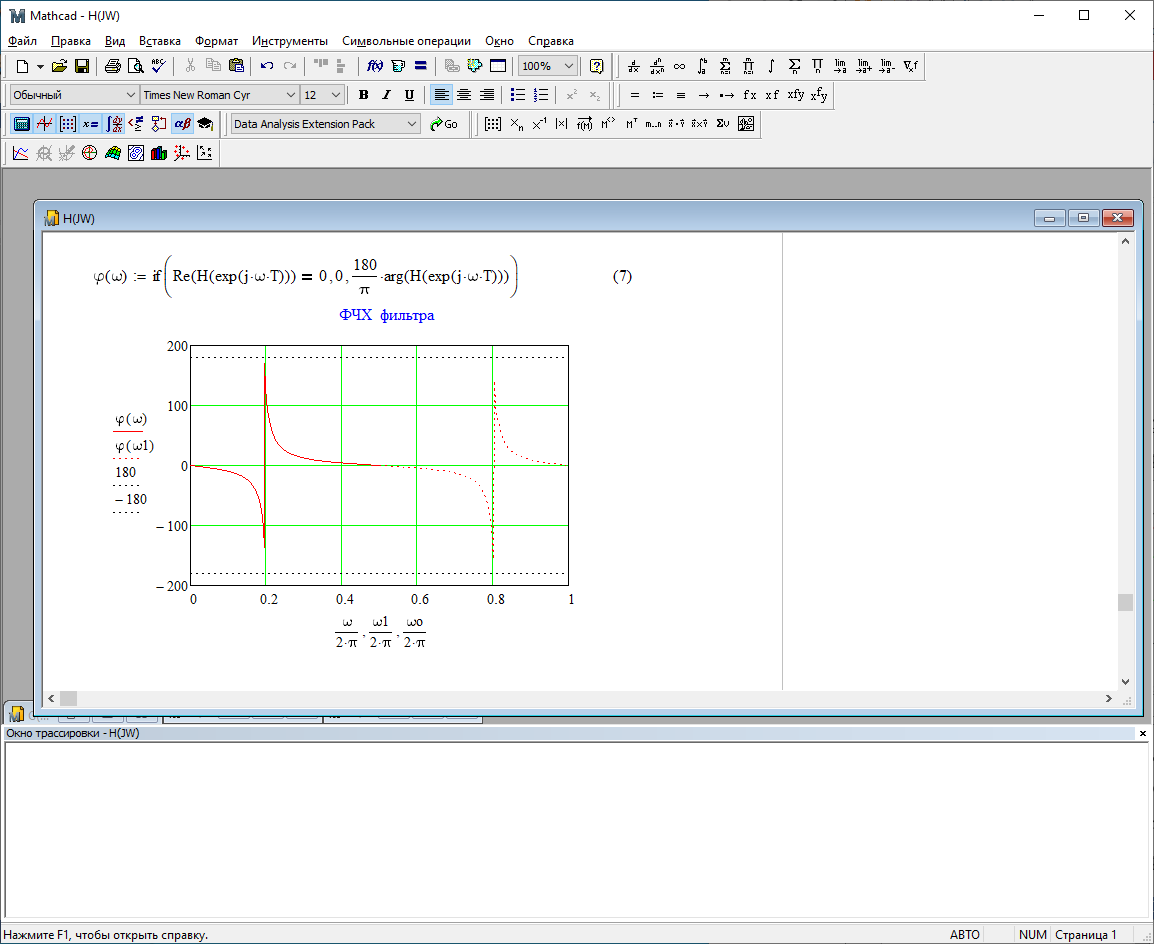
_{Рис.2.1 – АЧХ фильтра. Рис.2.2 – ФЧХ фильтра}.

Используя программный модуль h(nT) получим импульсную характеристику:



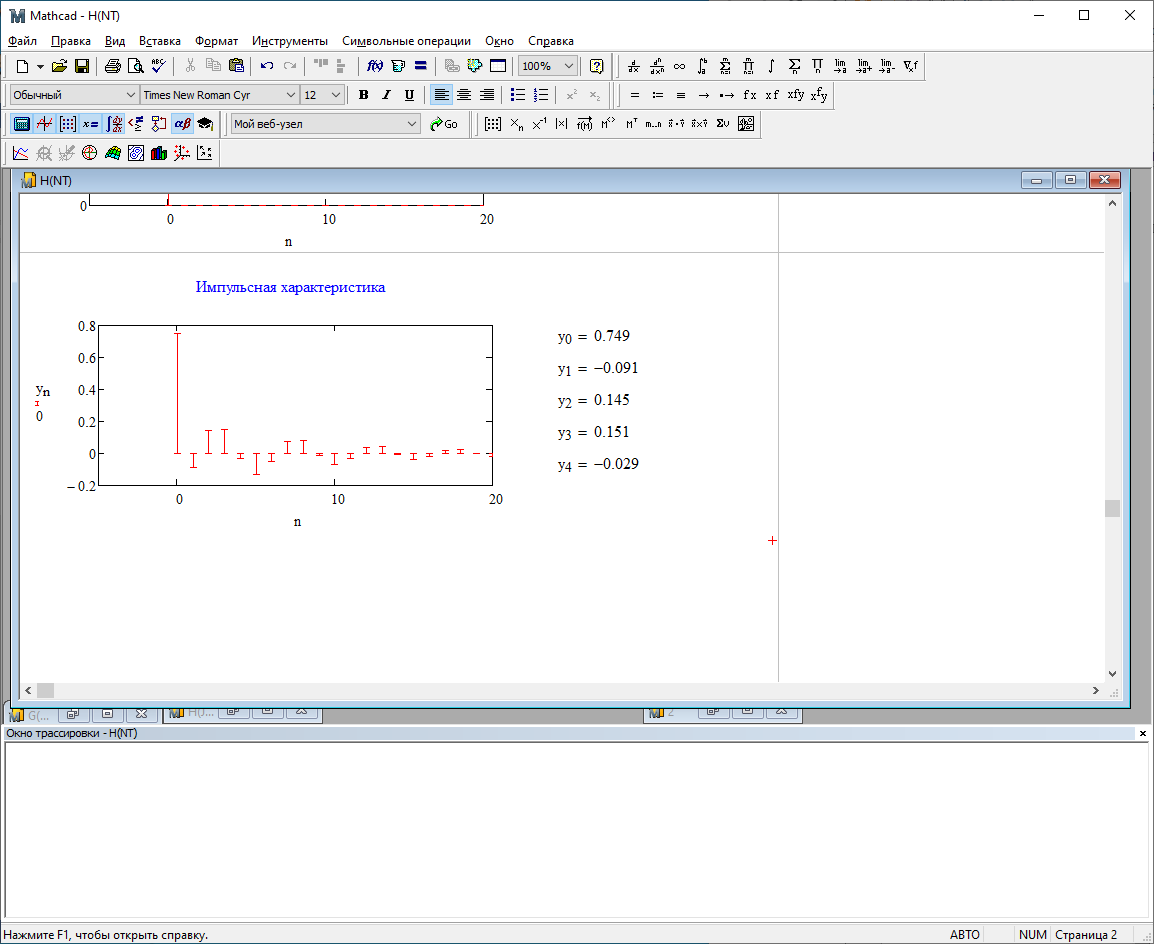
_{Рис.2.3 – Импульсная характеристика}.
Переходная характеристика:

Используя программный модуль g(nT) получим переходную характеристику:



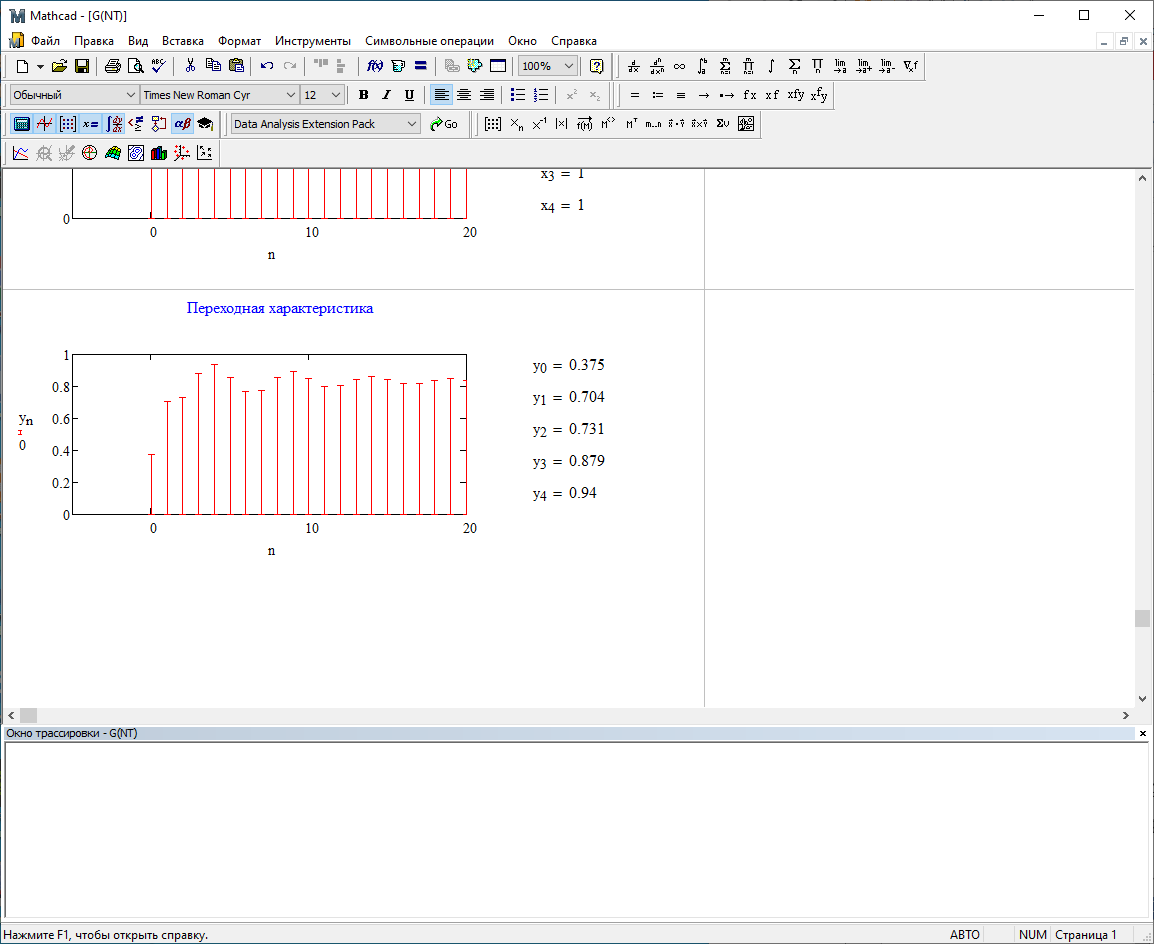
_{Рис.2.4 – Переходная характеристика}.

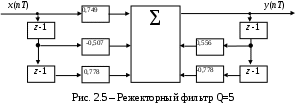
Структурная схема режекторного фильтра приведена на рис.2.5:
Изменим коэффициент b₁ = 0.177. Рассмотрим произошедшие изменения.

Импульсная характеристика:



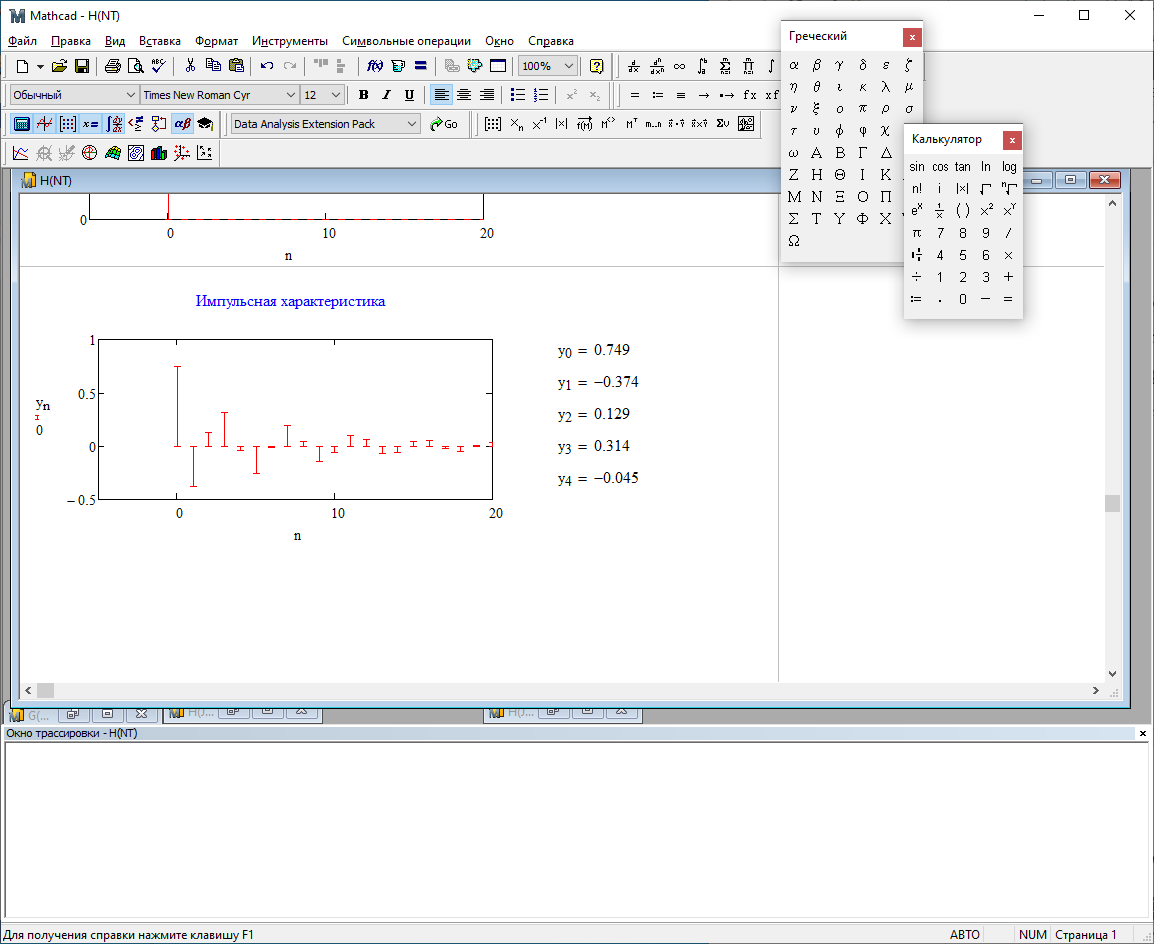
_{Рис.2.6 – Импульсная характеристика}.

Переходная характеристика:



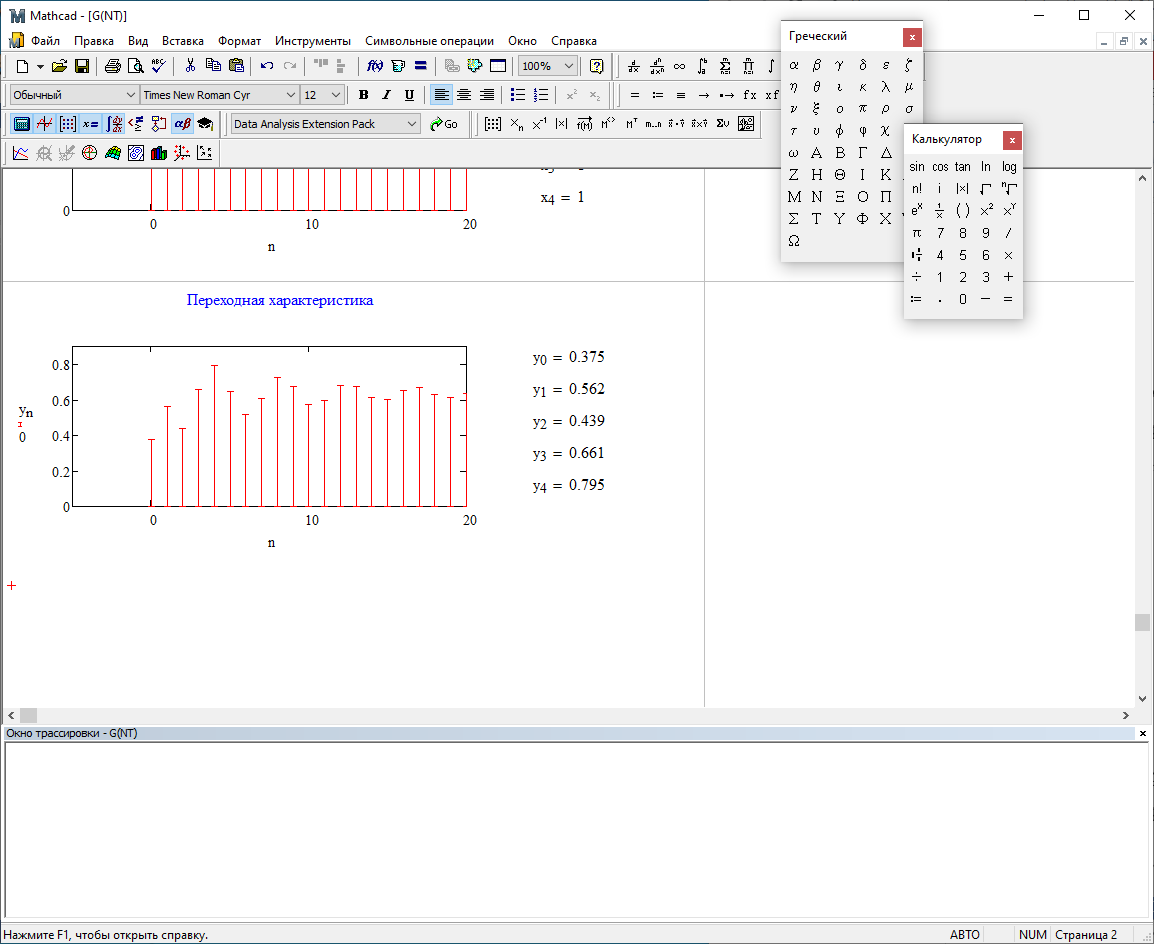
_{Рис.2.7 – Переходная характеристика}.
АЧХ и ФЧХ фильтра:

---

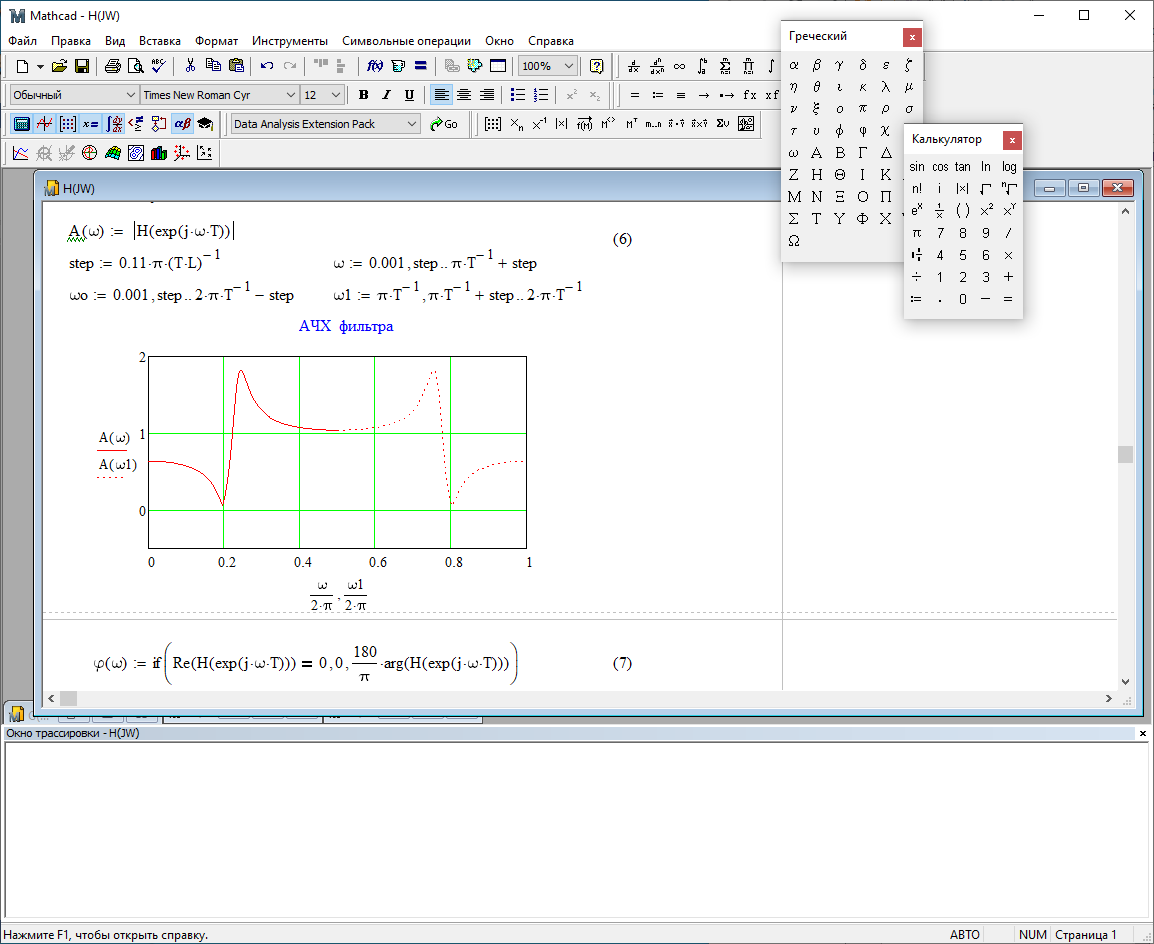
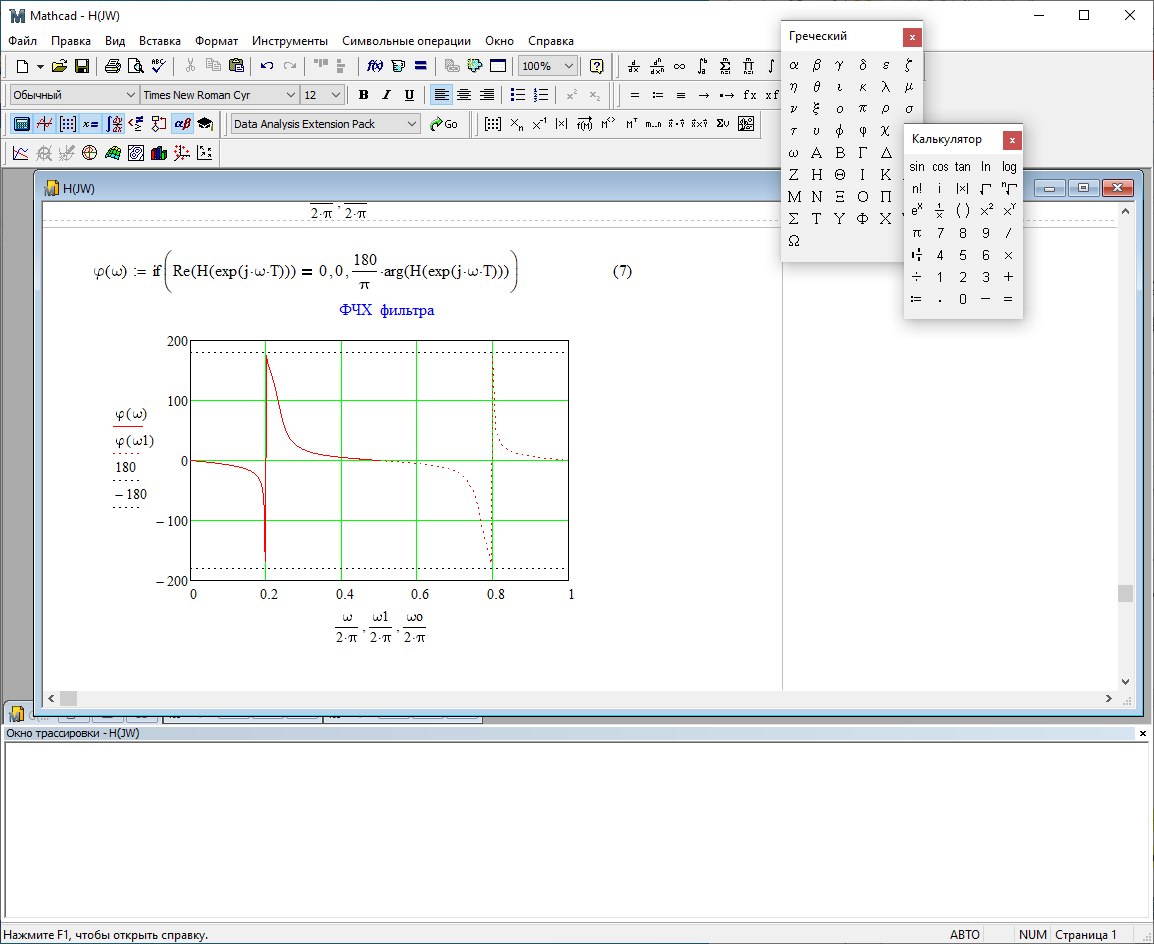
_{Рис.2.8 – АЧХ фильтра}. _{Рис.2.9 – ФЧХ фильтра}.
При уменьшении b₁ до 0,177 в ИХ и ПХ значительных изменений не наблюдается. изменился только первый отсчет. Стал выше, вследствие того, что мы увеличили а₀. АЧХ фильтра стала приближенной к АЧХ полосового фильтра поднялась с 1 до 1.2 на нижних и верхних частотах. ФЧХ фильтра изменилась незначительно. В области средних частот характеристика сильно исказилась. Появился «прогиб» характеристики вверх и вниз.
3. Дискретная свертка сигналов и входного сигнала с импульсной характеристикой ЦФ.

Зададим два входных сигнала:


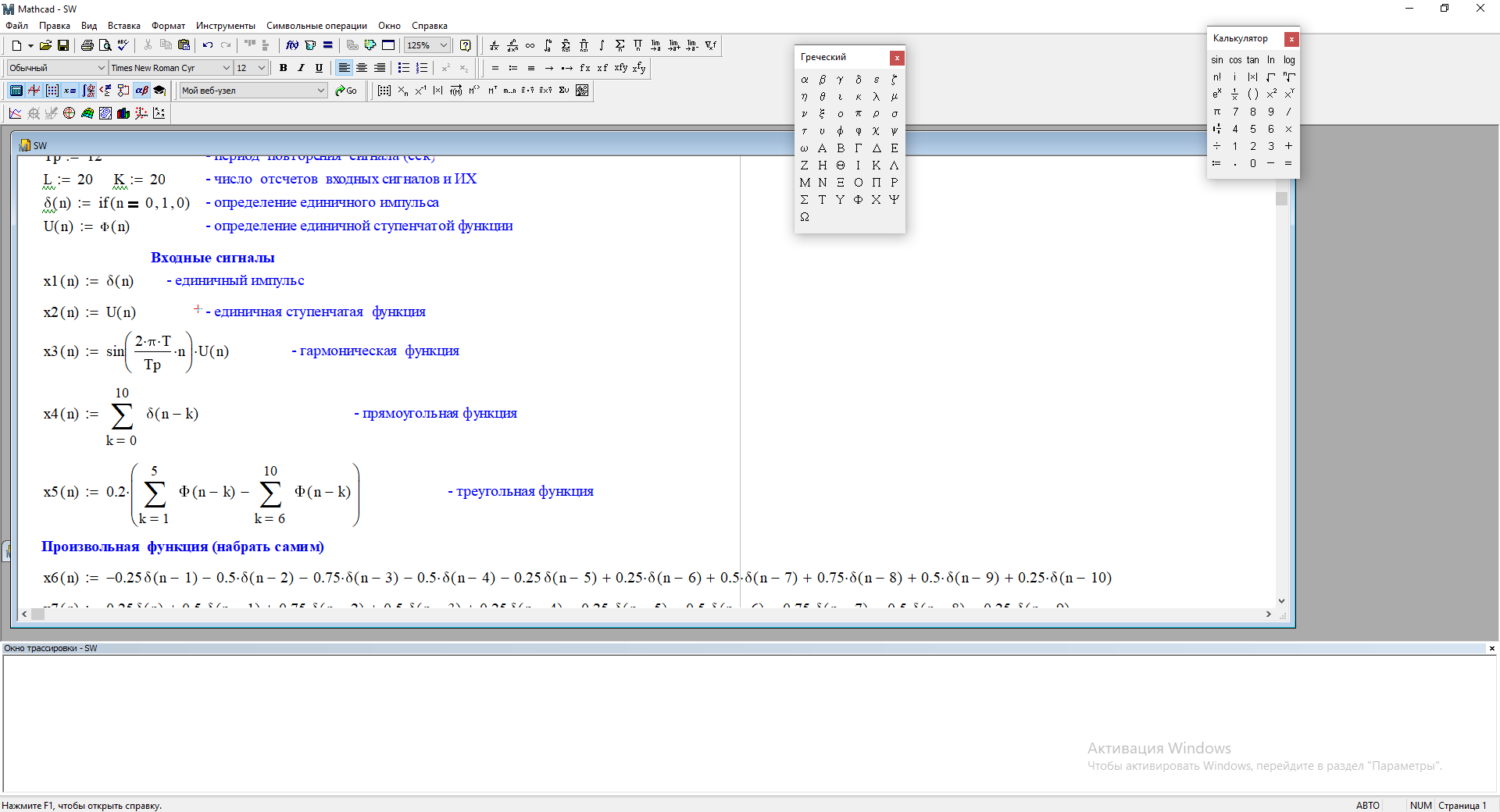
Используя программный модуль sw получим следующую свертку этих сигналов:



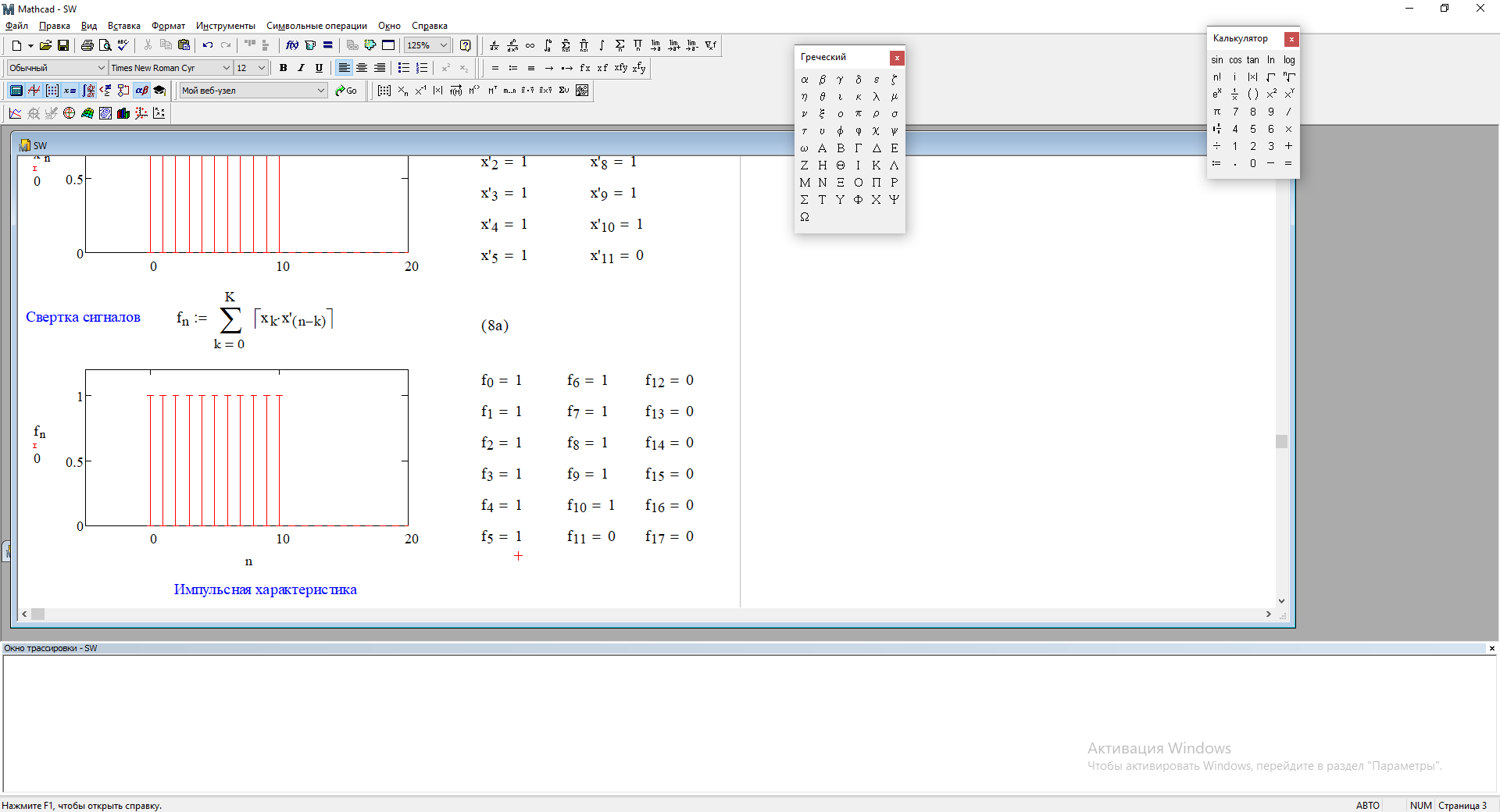
_{Рис. 3.1 – Свертка двух сигналов}.
Возьмем, из предложенных в задании, импульсную характеристику:


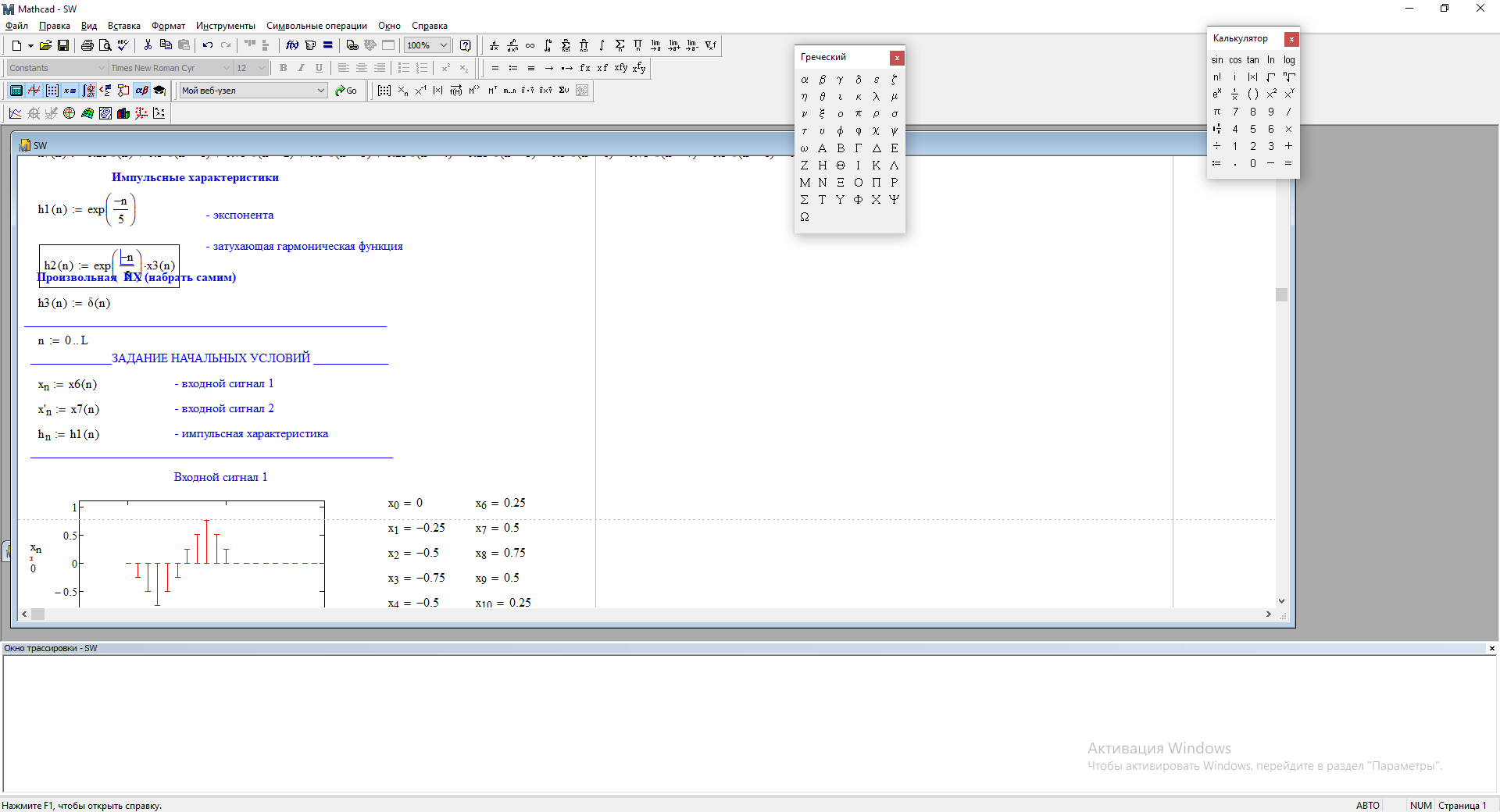
Получим выходной сигнал (свертку с импульсной характеристикой):



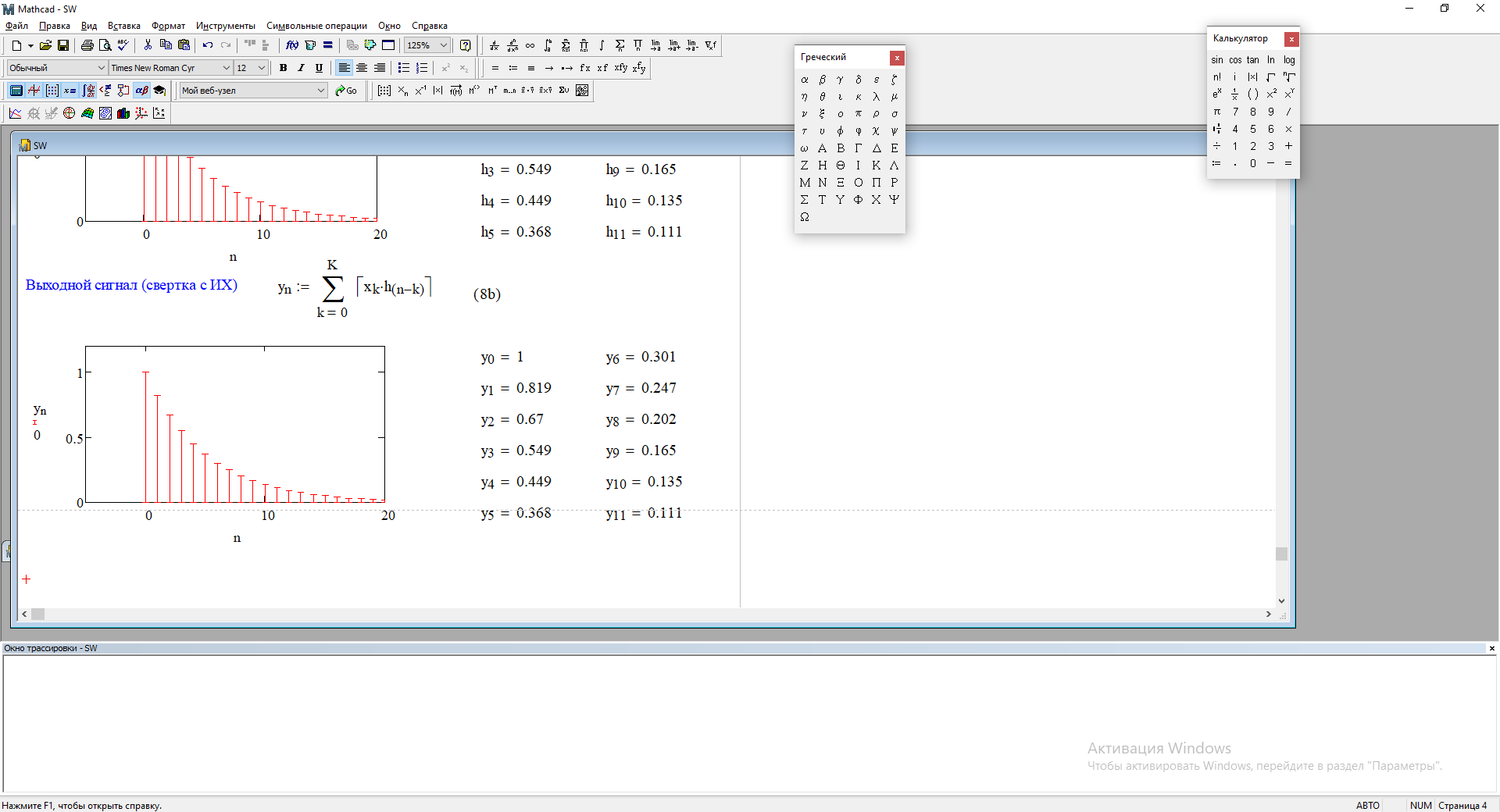
_{Рис.3.2 – Импульсная характеристика}. _{Рис.3.3 – Свертка с импульсной характеристикой.}

4. Дискретная свертка сигналов и входного сигнала с импульсной характеристикой ЦФ (сигналы взяты в соответствии с вариантом №5).

Аналитическое описание x6(n) через единичные импульсы будет иметь вид:

---

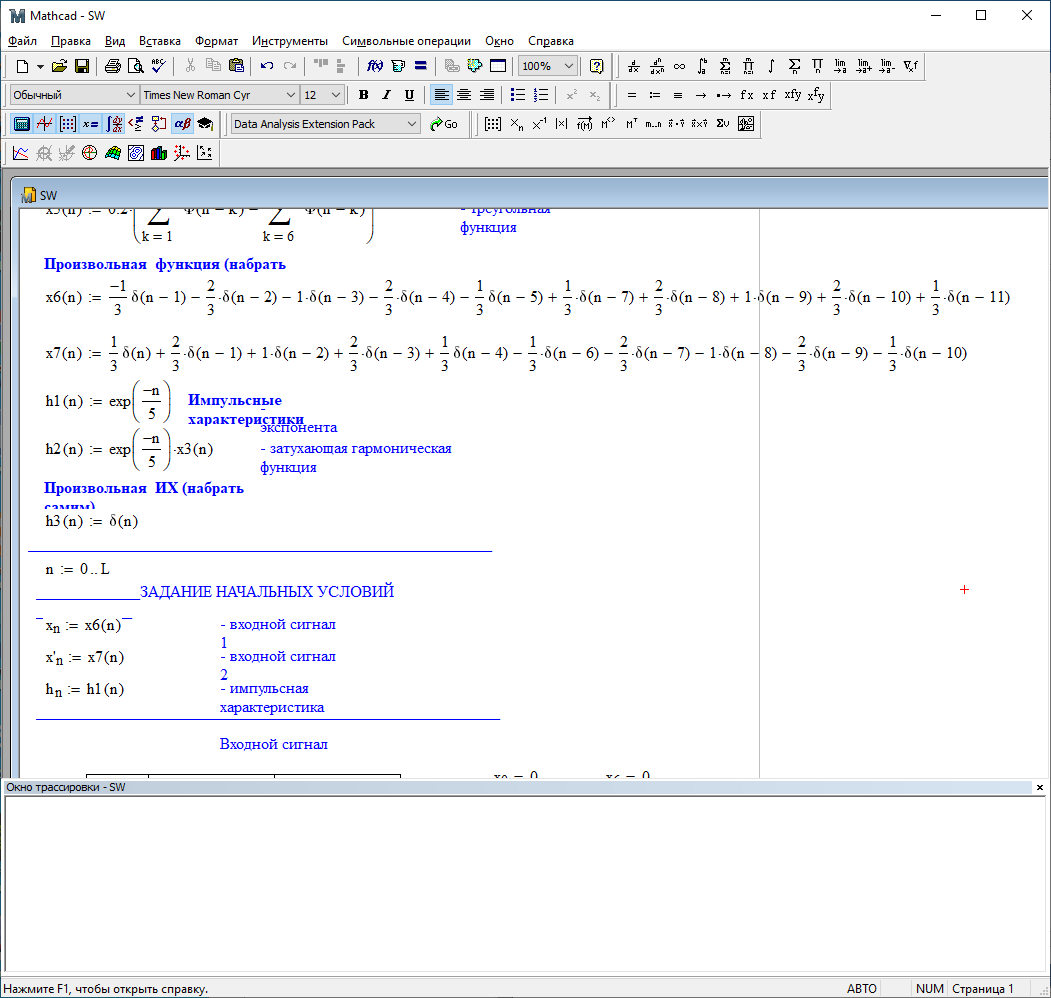
Симметричный ему сигнал x7(n) будет иметь вид:





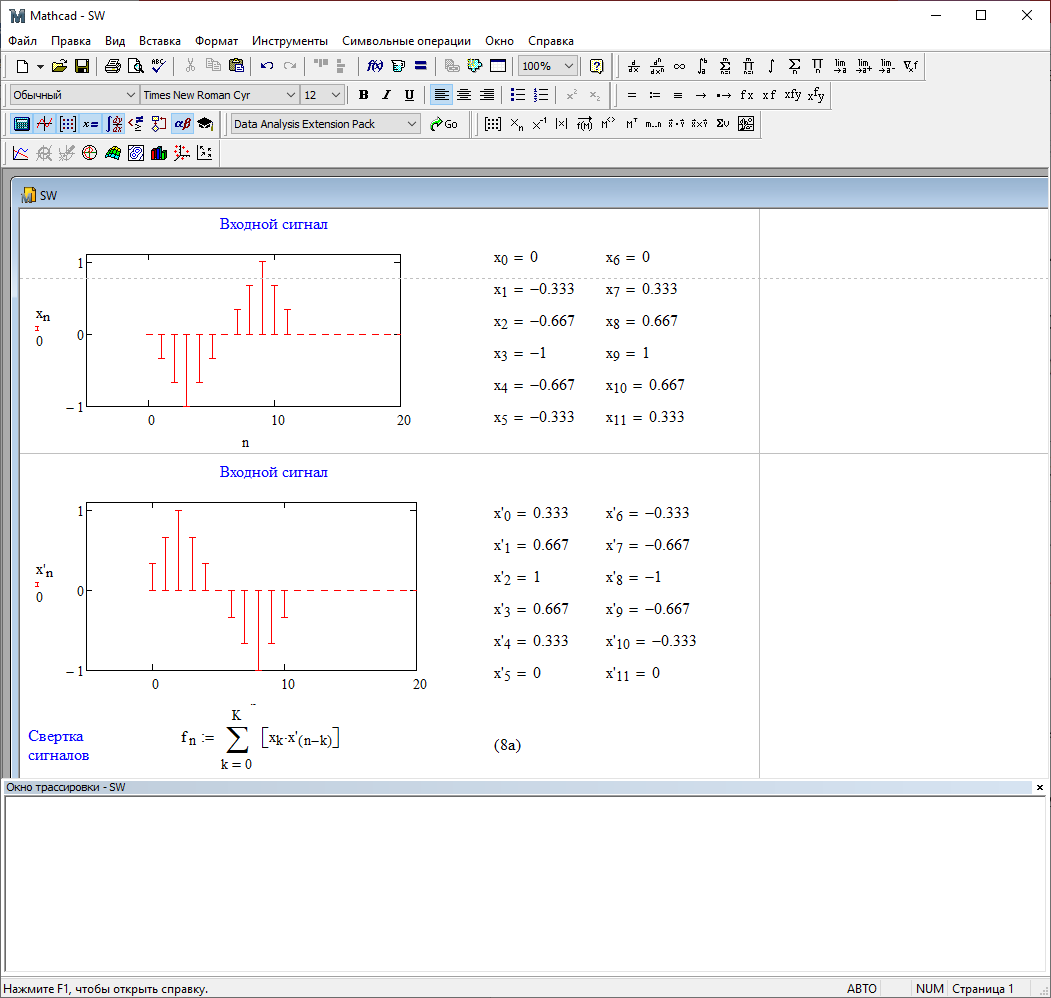
<sub>Рис. 4.1 – Сигнал x6(n)



Рис. 4.2 – Сигнал x7(n</sub>)
Дискретная свёртка данного сигнала с симметричным сигналом x7(n):



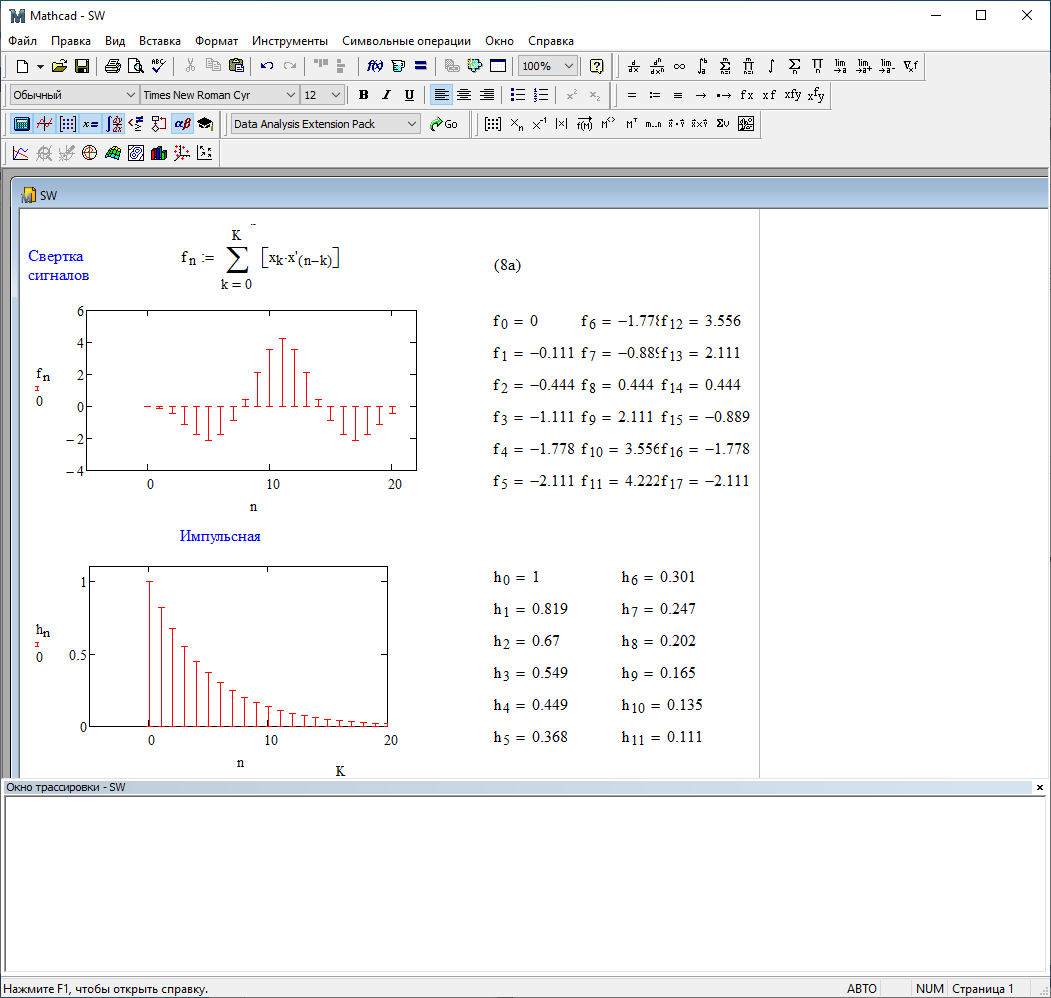
_{Рис. 4.3 – Свертка двух сигналов.}

Возьмем, из предложенных в задании, импульсную характеристику



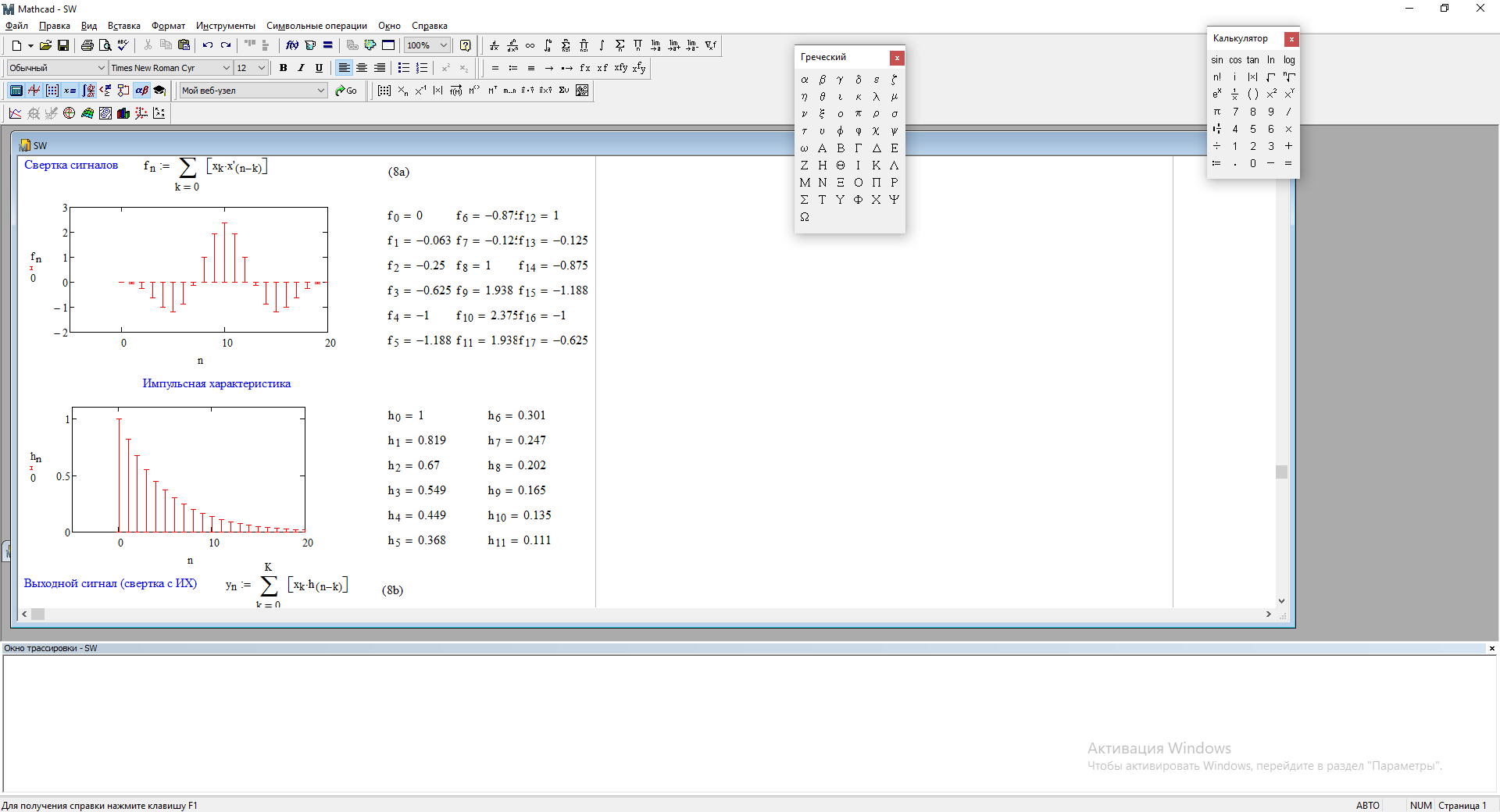
_{Рис. 4.4 – Импульсная характеристика}
Дискретная свёртка данного сигнала с импульсной характеристикой :



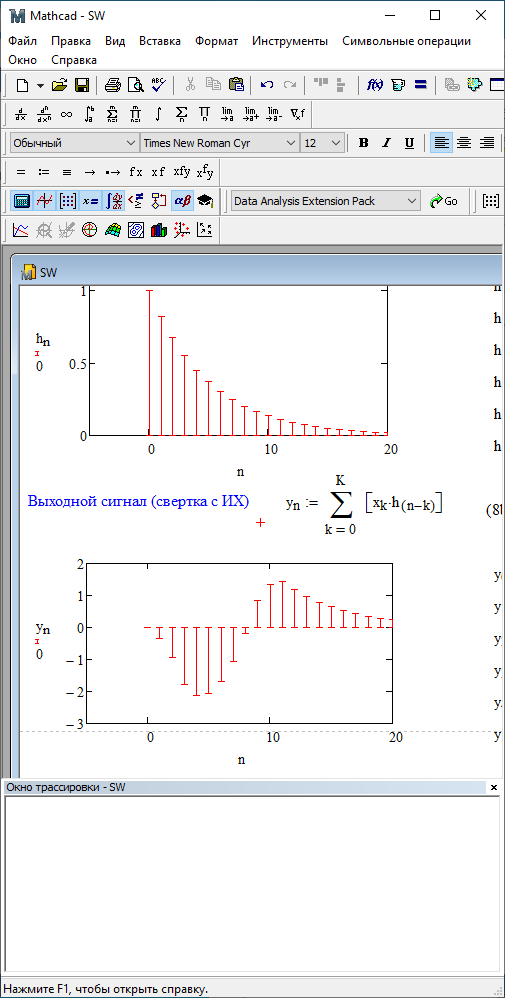
_{Рис. 4.5 – Дискретная свертка с ИХ}.
Возьмем другую импульсную характеристику:



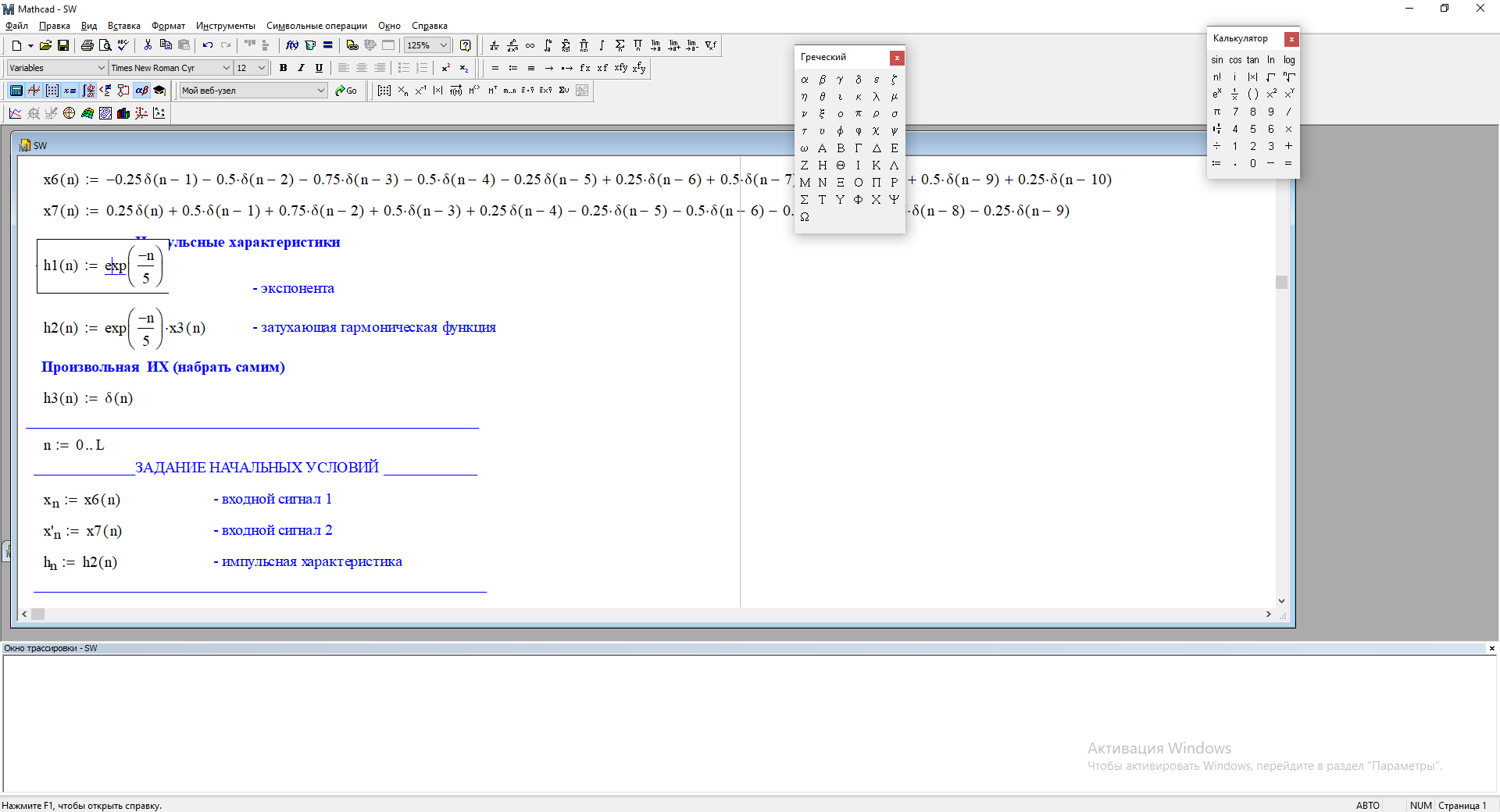
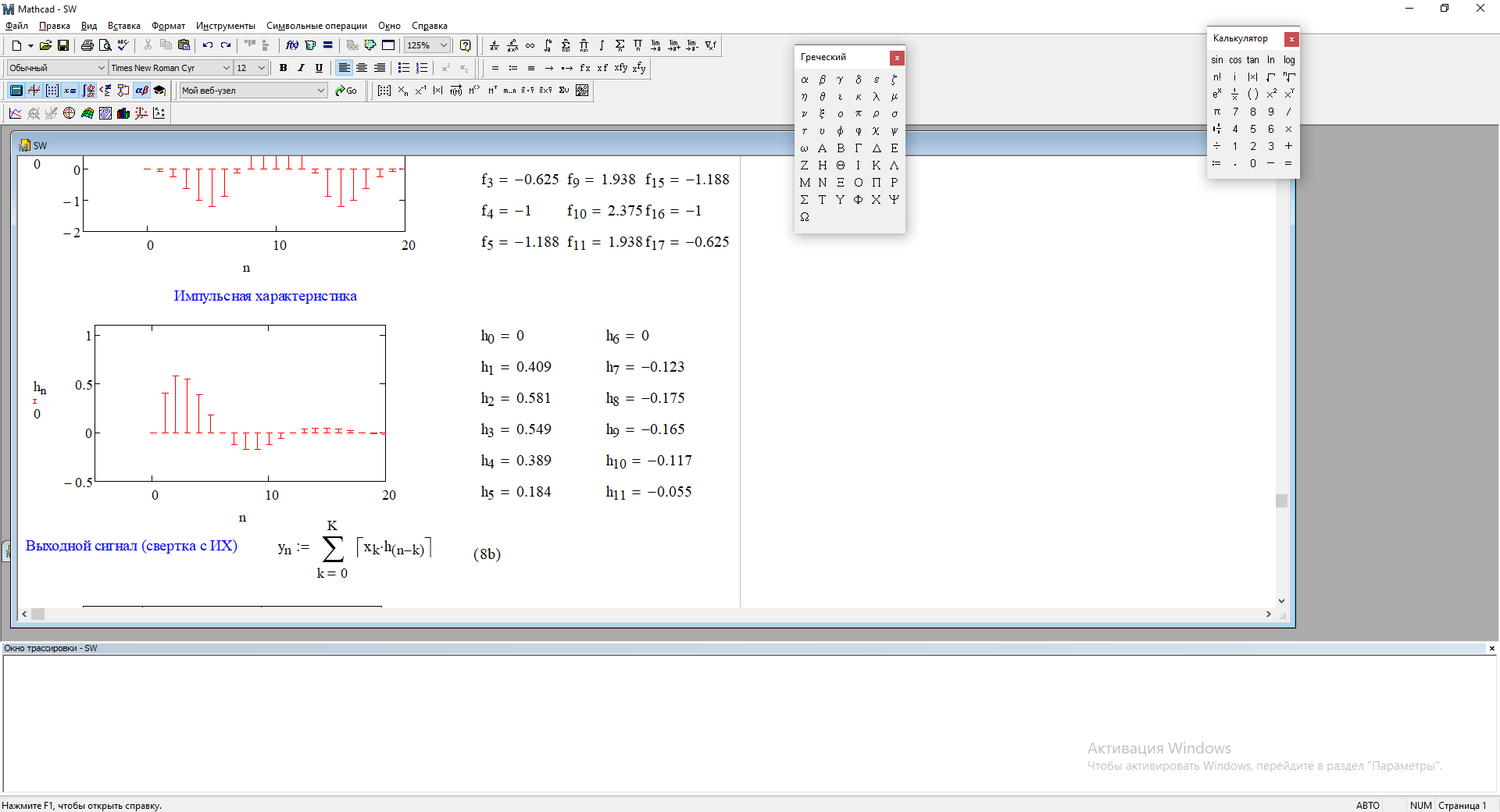
_{Рис. 4.6 – Импульсная характеристика}

Дискретная свёртка данного сигнала с импульсной характеристикой:



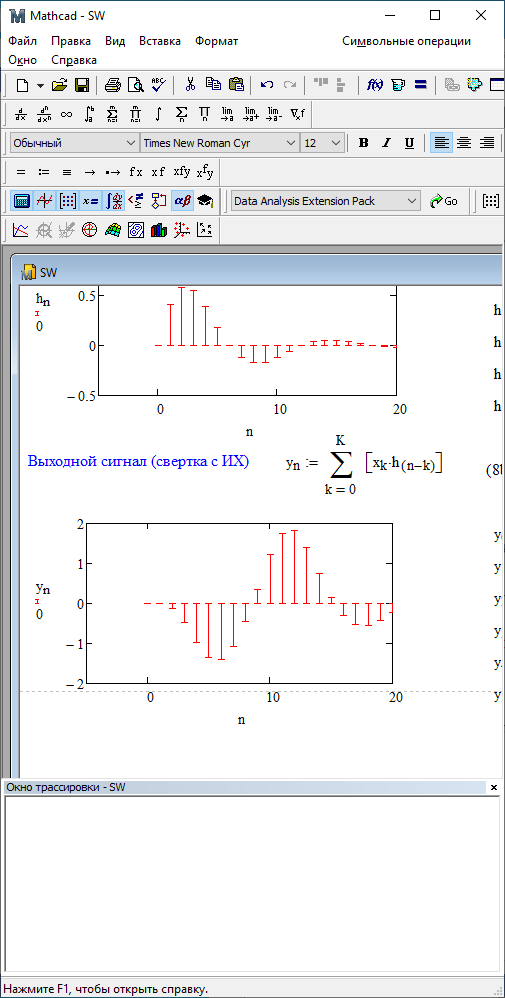
_{. Рис. 4.7 – Дискретная свертка с ИХ.}
5. Зависимость дисперсии шума квантования АЦП на выходе цифрового фильтра от коэффициента сглаживания K. Запишите выражение для системной функции H(z) и зарисуйте структурную схему ЦФ. Рассчитайте теоретически зависимость дисперсии шума квантования АЦП на выходе цифрового фильтра от коэффициента сглаживания K. Сравните расчет с полученными данными.
Исследуем зависимость дисперсии шума квантования АЦП сглаживающего звена от коэффициента К.

Структурная схема сглаживающего звена приведении на Рис.5.1:

---

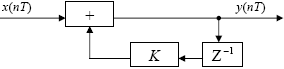
_{Рис.5.1 – Структурная схема сглаживающего звена.}
Системная функция сглаживающего звена:





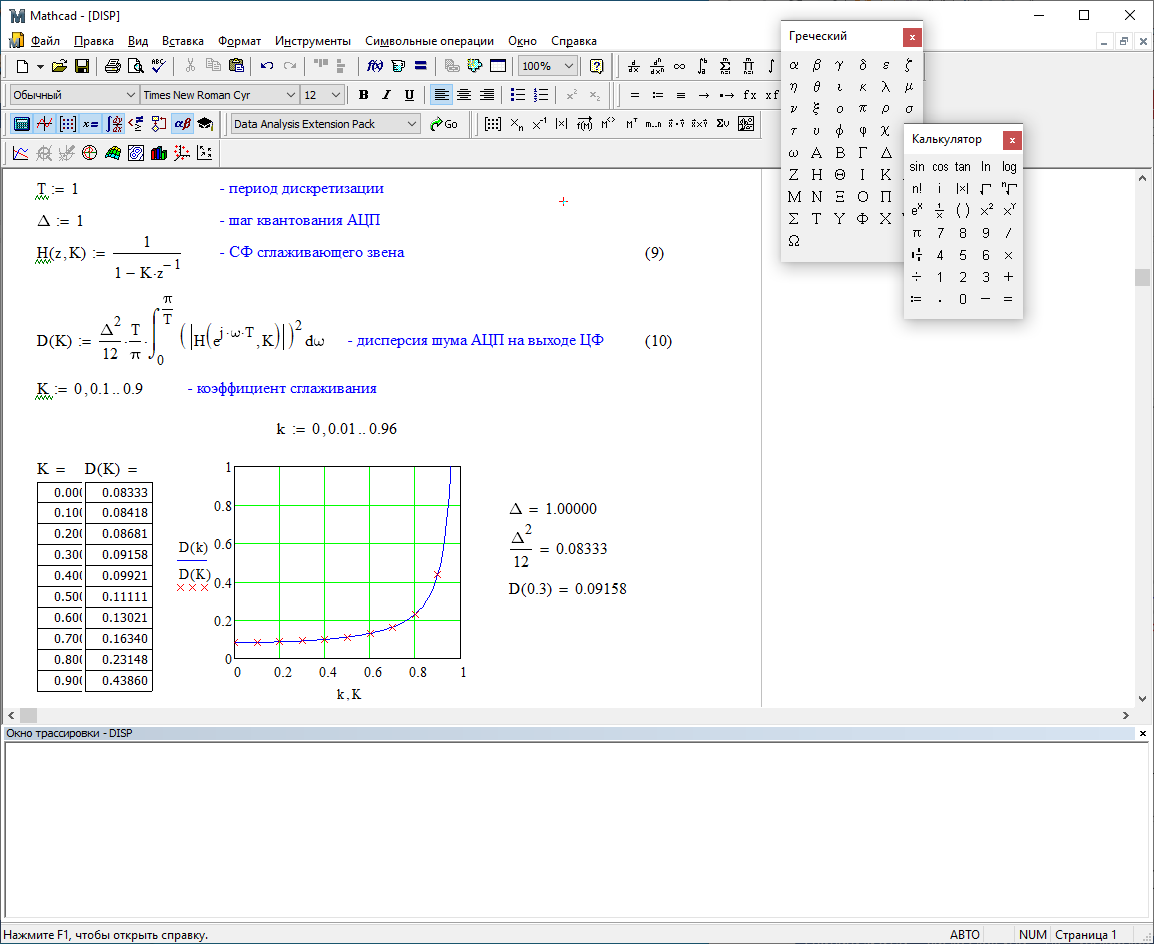
_{Рис. 5.1 – График зависимости дисперсии от коэффициента сглаживания К.}

Рассчитаем теоретически зависимость дисперсии шума квантования АЦП на выходе цифрового фильтра от коэффициента сглаживания K:













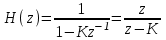
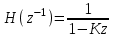
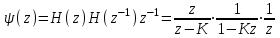
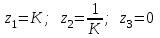
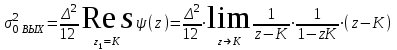
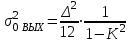
Расчетные и экспериментальные данные сведены в таблицу 5.1.
Таблица 5.1

K	0	0,1	0,2	0,3	0,4	0,5	0,6	0,7	0,8	0,9
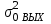теорет.	0,08333	0,08418	0,08681	0,09158	0,09921	0,11111	0,13021	0,16340	0,23148	0,43860
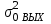экпер.	0,083	0,084	0,087	0,092	0,099	0,111	0,130	0,163	0,231	0,439

Можно заметить, что эти данные, с большой степенью точности совпадают.
6. Просмотрите поля ошибок, вычисленные программными модулями graf1, graf2, graf3. Зарисуйте эти поля ошибок и объясните функциональные зависимости от значений коэффициентов b

---

Смотрите также файлы

• Практическое задание 2, Модуль Общий план строения центральной нервной системы. Спинной мозг слушатель Федина Татьяна Андреевна Преподаватель Пузикова Ольга Юрьевна.docx

• Программа занятий специального педагога с Кулиевой Фахриёй 1 класс на 1 четверть 2022 2023 учебного года.docx

• 1. Как вы понимаете значение терминов объект управления исубъект управления.docx

• Реферат на тему Концепции и функции менеджмента.docx

• Как простой родник в белгородской глубинке превратился в святой источник.docx