МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ

Федеральное государственное бюджетное

образовательное учреждение высшего образования

«НОВОСИБИРСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ»

Кафедра менеджмента

КОНТРОЛЬНАЯ РАБОТА

Дисциплина: Эконометрика

Направление подготовки: 38.03.02 Менеджмент

Выполнил:		Проверил:
Студент	Мешкова А.	Преподаватель	Щеколдин В.Ю.
Факультет	ЗО ИДО
Направление (специальность) подготовки	38.03.02 Менеджмент	Балл:________		, ECTS: ________
Группа	ДЭ-060	Оценка: _________________
Шифр	093406703
____________________________________		____________________________________
подпись		подпись
Дата сдачи:	«__»__________2022 г.	Дата защиты:	«__»__________2022 г.

Новосибирск 2022

Задача. Построить и проинтерпретировать модель взаимосвязи между указанными факторами, проверить на значимость, осуществить точечный и интервальный прогноз, сделать выводы.

ПОРЯДОК РЕШЕНИЯ

1. Исходные данные нанести на координатную плоскость. Сделать предварительное заключение о наличии взаимосвязи между факторами X и Y, о ее характере (положительная или отрицательная) и форме (линейная или нелинейная).

2. Рассчитать значение парного коэффициента корреляции xy r . Используя t-критерий Стьюдента проверить значимость полученного коэффициента корреляции и сделать вывод о тесноте связи между факторами X и Y.

3. Полагая, что взаимосвязь между факторами X и Y

---

может быть описана линейной функцией, записать соответствующее уравнение этой зависимости. Вычислить оценки неизвестных параметров уравнения парной регрессии по методу наименьших квадратов на основе решения системы нормальных уравнений. Проинтерпретировать полученные результаты в терминах решаемой задачи.

4. Проверить значимость всех параметров модели по t-критерию Стьюдента. Для значимых коэффициентов построить доверительные интервалы. Сформулировать выводы.

5. Проверить значимость модели (уравнения регрессии) в целом с помощью F-критерия Фишера. Сформулировать вывод.

6. Построить таблицу дисперсионного анализа.

7. Выбрать прогнозную точку x P в стороне от основного массива данных. Используя уравнение регрессии выполнить точечный прогноз величины Y в точке x P .

8. Рассчитать доверительные интервалы для уравнения регрессии и для результативного признака y P при доверительной вероятности a = 0.95.

9. Изобразить в одной системе координат исходные данные, линию регрессии, точечный прогноз, 95% доверительный интервал.

10. Сделать общие выводы по проделанной работе.

Таблица 1 - Исходные данные

Код	Стоимость основных производственных фондов (Х, тыс. руб.)
М	358	338	425	413	508	485	548	613	723	750
	Среднесуточная производительность (Y, тонн)
А	69	71	70	72	73	68	72	75	76	76

РЕШЕНИЕ

1. 
   Необходимо нанести исходные данные на координатную плоскость:
   

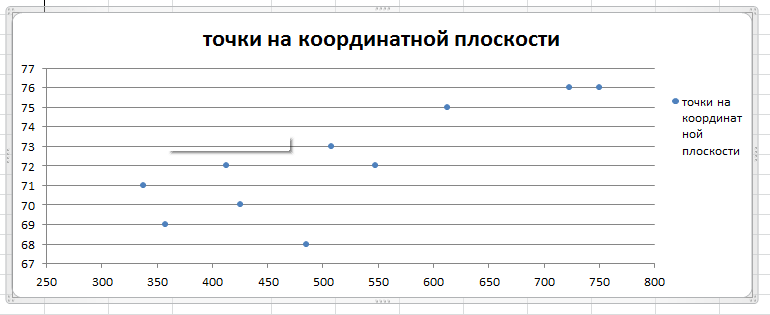
Рисунок 1 – Исходные данные, нанесенные на координатную плоскость

Предварительное заключение: существует взаимосвязь между факторами Х и Y, ее характер: положительная, так как значения Х и Y возрастают, форма взаимосвязи – линейная, так как форма напоминает прямую линию.

---

2. 
   Далее я построила таблицу и рассчитала значение парного коэффициента корреляции r_xy.
   

Таблица 2 – Расчетная таблица №1

х	у	x2	y2	x*y
358	69	128164	4761	24702
338	71	114244	5041	23998
425	70	180625	4900	29750
413	72	170569	5184	29736
508	73	258064	5329	37084
485	68	235225	4624	32980
548	72	300304	5184	39456
613	75	375769	5625	45975
723	76	522729	5776	54948
750	76	562500	5776	57000
5161	722	2848193	52200	375629

Парный коэффициент корреляции рассчитывается по формуле: r_xy = ,

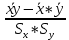где ,

,

---

,

,



=

=

=

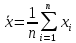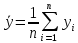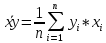
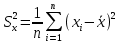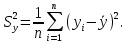
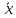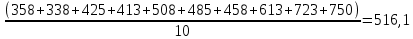
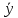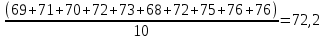
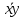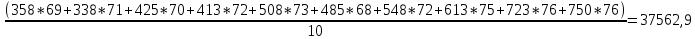
Дисперсии:





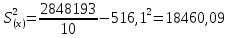
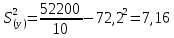
Среднеквадратическое отклонение:

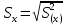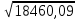= = 135,868

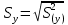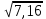= = 2,676

Коэффициент корреляции:

r_{xy= .}

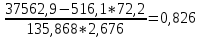Коэффициент корреляции может принимать значения от -1 до 1. В моем случае значение коэффициента положительное, близится к 1, что говорит о тесной, прямой связи между признаками Х и Y.

Используя t-критерий Стьюдента проверяю значимость рассчитанного коэффициента корреляции. Для этого предполагаю, что есть нулевая гипотеза H₀, где нет линейной взаимосвязи между признаками. Она подтвердится в случае, если наблюдаемое значение критерия будет меньше, чем значение критерия Стьюдента по таблице. Уровень значимости а=0,05, число степеней свободы k=10-2=8.

t_табл(k;a:2); t_табл=(8;0,025)=2,752.

t_набл= r_{xy 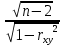;} t_набл=0,826 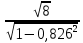=4,153

Если | t_набл |> t_крит , то есть основания отвергнуть нулевую гипотезу. t_табл =2,752. 5,637>2,752, нулевую гипотезу можно отвергнуть, а это значит что коэффициент корреляции не равен нулю и статистически значим.

3. 
   При помощи МНК записываю уравнение линейной регрессии y = bx+a. Для этого вычисляю параметры a, b, которые нужны для записи уравнения.
   

---

10a + 5161b = 722 |*(-516.1) -5161a - 2663592.1b = -372624.2

5161a + 2848193b = 375629 <=> 5161a + 2848193b = 375629

Решаю систему способом сложения:

-2663592,1b+2848193b = -372624.2+375629

184600.9b = 3004.8

b = 0.0162773

10a + 5161*0.01628 = 722

10a = 637.993

a = 63.7993

Уравнение регрессии: y=0.0162773x+63.7993.

Уравнение описывает следующее отношение: при увеличении стоимости основных производственных фондов (Х) на 1 тысячу рублей, среднесуточная производительность (Y) будет увеличиваться в среднем на 0,0162773 тонн. Значение коэффициента а = 63,7993 показывает прогнозируемый уровень среднесуточной производительности (Y).

4. 
   Проверяю значимость параметров а и b по t-критерию Стьюдента.
   

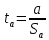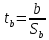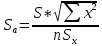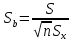; ; ; , где S-стандартная ошибка.

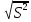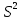S= , где -дисперсия ошибки регрессии.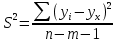



Таблица 3 – Расчетная таблица №2

x	y	y(x)	(yi-ycp)2	(y-y(x))2
358	69	69,627	10,24	0,393
338	71	69,301	1,44	2,887
425	70	70,717	4,84	0,514
413	72	70,522	0,04	2,185
508	73	72,068	0,64	0,868
485	68	71,694	17,64	13,644
548	72	72,719	0,04	0,517
613	75	73,777	7,84	1,495
723	76	75,568	14,44	0,187
750	76	76,007	14,44	0,00005
5161	722	722	71,6	22,69

---

Смотрите также файлы

• Анализ контрольной работы за 1 полугод.docx

• Автономная некоммерческая профессиональная образовательная организация "Национальный социальнопедагогический колледж" открытый социальноэкономический колледж.docx

• Математические методы в психологии.docx

• Преобразователи движения. Передачи с гибкой связью.docx

• Задание и два вопроса из раздела вопросы для проверки и письменно дайте на них развёрнутые ответы. Оформите файл в word.docx