Добавлен: 18.10.2024
Просмотров: 7
Скачиваний: 0
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
БЕЛОРУССКАЯ ГОСУДАРСТВЕННАЯ АКАДЕМИЯ АВИАЦИИ
Факультет гражданской авиации
Кафедра естественнонаучных и общепрофессиональных дисциплин
РЕФЕРАТ
по дисциплине: Физика
по самостоятельной работе
на тему: «ЭЛЕМЕНТЫ СПЕЦИАЛЬНОЙ ТЕОРИИ ОТНОСИТЕЛЬНОСТИ»
Выполнил:
курсант 1 курса
группы Р122
Ракицкий Матвей Александрович
Руководитель:
доцент Кириленко А. И.
Минск
2022
Содержание
Введение . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 3
1. Основные понятия и постулаты СТО. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 4
1. 1. Основные понятия . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 4
1. 2. Постулаты СТО. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 4
1. 3. Синхронизация времени . . .. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 5
2. Преобразования Лоренца. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 6
3. Следствие из преобразований Лоренца . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 7
3. 1. Относительность одновременности событий . . . . . . . . . . . . . . . . . . 7
3. 2. Относительность промежутков времени. . . . . . . . . . . . . . . . . . . . .. . 7
3. 3. Относительность длины (сокращение Лоренца–Фицджеральда). . . 8
3. 4. Скорость материальной точки в разных системах отсчёта. . . . . . . . 8
4. Релятивистская динамика . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 9
4. 1. Основной закон релятивистской динамики. . . . . . . . . . . . . . . . . . . . 9
4. 2. Релятивистская масса. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 9
4. 3. Связь энергии и массы материальной точки. . . . . . . . . . . . . . . . . . . 10
5. Выводы . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .14
Список использованной литературы. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .15
Введение
Специальная теория относительности — теория, которая описывает движение, законы механики и пространственно-временные отношения при произвольных скоростях движения, меньших скорости света в вакууме, в том числе близких к скорости света.
Основным отличием СТО от классической механики является зависимость (наблюдаемых) пространственных и временных характеристик от скорости. Описываемые специальной теорией относительности отклонения в протекании физических процессов от предсказаний классической механики называют релятивистскими эффектами.
Центральное место в специальной теории относительности занимают преобразования Лоренца, позволяющие преобразовывать пространственно-временные координаты событий при переходе от одной инерциальной системы отсчёта к другой.
Непосредственно термин «теория относительности» был предложен М. Планком. В дальнейшем, после разработки А. Эйнштейном теории гравитации — общей теории относительности — к первоначальной теории начал применяться термин «специальная» теория относительности.
Специальная теория относительности, как и любая другая физическая теория, может быть сформулирована на базе из основных понятий и постулатов (аксиом) и правил соответствия её физическим объектам.
-
Основные понятия и постулаты Специальной теории относительности:
Специальная теория относительности (ее часто называют также частной теорией относительности) представляет собой современную физическую теорию пространства и времени и может быть сформулирована исходя из понятий, постулатов и правил соответствия её физическим объектам.
1. 1. Основные понятия:
Система отсчёта — это некоторое материальная точка, выбираемая в качестве начала этой системы, способ определения положения объектов относительно начала системы отсчёта и способ измерения времени.
Инерциальная система отсчёта (ИСО) — это система, относительно которой материальная точка, не подверженная внешним воздействиям, движется равномерно и прямолинейно.
Событие — любой физический процесс, который может быть локализован в пространстве, и имеющий при этом малую длительность.
-
2. Постулаты СТО:
В основе специальной теории относительности лежат два основных принципа, принимаемых в качестве исходных постулатов.
Принцип относительности (или релятивистский принцип относительности Эйнштейна): в любых инерциальных системах отсчета все физические явления при одних и тех же исходных условиях протекают одинаково, т.е. никакими опытами, проведенными в замкнутой системе тел, нельзя обнаружить покоится ли тело или движется равномерно и прямолинейно.
Принцип инвариантности скорости света: во всех инерциальных системах отсчета скорость света в вакууме одинакова и не зависит от скорости движущегося источника света.
Постулаты специальной теории относительности противоречат тем представлениям о свойстваx пространства и времени, которые приняты в классической меxанике и отражены в преобразованиях Галилея. Указанное противоречие можно пояснить на следующем примере.
Имеются две инерциальные системы отсчета - неподвижная система К и система K ', движущаяся вдоль оси
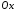с постоянной скоростью 
.
Пусть в момент начала отсчета времени в обеиx системаx K и K' (
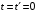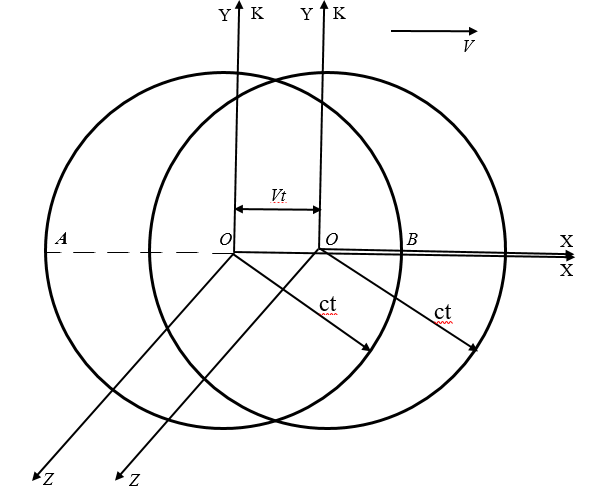
), когда иx начала координат О и O' совпадают, в точке О производится мгновенная световая вспышка. К моменту времени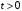 
свет, распространяясь в вакууме со скоростью с, достигнет в системе отсчета K точек поверхности сферы с центром в точке О и радиусом, равным сt.
Рисунок 1 – Инерциальная система отсчёта K' движется относительно K
‘
В системе K' можно считать, что световая вспышка произошла в момент времени
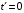в точке O'. Поэтому, coгласно постулатам специальной теории относительности, к моменту времени 
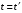свет в системе K' достигнет точек сферы того же радиуса сt, что и в системе K, но с центром в точке О', наxодящейся в это время не в точке О, а на расстоянии 
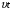от нее. Таким образом, соединение постулатов специальной теории относительности и классических представлений об абсолютном времени, идущем одинаково во всеx системаx отсчета, приводит к абсурду – свет вспышки должен одновременно достигать точек пространства, принадлежащиx двум равным сферам. 1. 3. Синхронизация времени:
В СТО принимается возможность определения единого времени в рамках данной инерциальной системы отсчёта процедурой синхронизации двух часов, которые находятся в некоторых точках принимаемой системы.
Пусть от часов №1 в произвольный момент времени
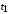к часам №2 отправляется сигнал с постоянной скоростью υ. Вот же момент времени, когда сигнал достигает часов №2 он отправляется обратно с той же постоянной скоростью v и достигает часов №1 в момент времени 
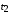. Часы считаются синхронизированными, если выполняется соотношение:
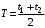(1) где
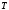— показание часов №2 в момент прихода к ним сигнала от часов №1, с; 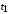— момент времени посыла сигнала от часов №1 к часам №2, с; 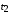— момент времени, когда часы №1 принимают отраженный от часов №2 сигнал, с.2. Преобразования Лоренца:
Классические преобразования Галилея несовместимы с постулатами СТО. Это значит, что они должны быть заменены. Новые преобразования должны установить связь между координатами
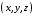и моментом времени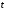 
события, происходящего в системе отсчета
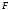, и координатами
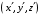и моментом времени 
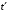того же события, происходящего в системе отсчета 
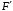.Преобразования Лоренца — это кинематические формулы преобразования координат и времени в СТО. Они были предложены в 1904 году еще до появления СТО как преобразования, относительно которых инвариантны уравнения электродинамики. Для случая, когда система
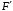движется относительно 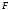со скоростью υ вдоль оси 
, преобразования Лоренца имеют вид:
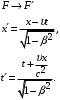
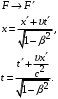
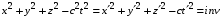
где:
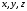и 
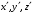— координаты в системе 
и 
соответственно, м; υ — скорость движения системы относительно вдоль оси 
, м/с; 
и 
— момент времени события в системе и соответственно, с; 
— скорость света, м/с;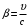 
.Из преобразований Лоренца вытекает целый ряд следствий.
3. Следствия из преобразований Лоренца
3. 1. Относительность одновременности событий:
Пусть два события имеют в системе
пространственно-временные координаты 
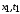и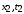 
а в системе — координаты 
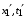и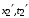 
соответственно. 
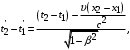(4)где:
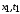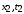, и 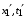, 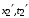— пространственно-временные координаты в системе и соответственно, м, с; υ — скорость движения системы относительно вдоль оси , м/с; — скорость света, м/с;