Добавлен: 18.10.2024
Просмотров: 8
Скачиваний: 0
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
3. 2. Относительность промежутков времени:
Пусть в одной и той же точке в системе F' происходят два события, разделённые промежутком времени
 (
(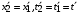 ). Предположим, что эта система связана с ракетой, летящей со скоростью υ относительно Земли, и пусть упомянутые два события — космонавт покинул кресло, космонавт вернулся в кресло. Система
). Предположим, что эта система связана с ракетой, летящей со скоростью υ относительно Земли, и пусть упомянутые два события — космонавт покинул кресло, космонавт вернулся в кресло. Система  — система покоя для данных событий, они происходят в одной и той же точке. Промежуток времени между двумя событиями в системе покоя называют собственным временем.
— система покоя для данных событий, они происходят в одной и той же точке. Промежуток времени между двумя событиями в системе покоя называют собственным временем. Теперь обратимся к системе отсчёта
 , связанной в данном случае с Землёй. Взятые события, если их рассматривать с Земли, будут происходить в разных пространственных точках:
, связанной в данном случае с Землёй. Взятые события, если их рассматривать с Земли, будут происходить в разных пространственных точках: 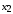 и
и 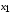 . По часам наблюдателя с Земли эти события разделяет промежуток времени
. По часам наблюдателя с Земли эти события разделяет промежуток времени 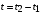 .
.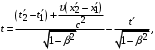 (5)
(5)где:
 — промежуток времени, разделяющий два события в системе
— промежуток времени, разделяющий два события в системе  , с;
, с;  ,
,  и
и  ,
,  — пространственно-временные координаты в системе
— пространственно-временные координаты в системе  и
и  соответственно, м, с; υ — скорость движения системы
соответственно, м, с; υ — скорость движения системы  относительно
относительно  вдоль оси
вдоль оси  , м/с;
, м/с;  — скорость света, м/с;
— скорость света, м/с;  .
.
Промежуток времени между двумя событиями зависит от системы отсчёта.
3. 3. Относительность длины (сокращение Лоренца–Фицджеральда):
Пусть тело покоится в системе
 , его собственная длина
, его собственная длина 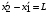 . Выполним его «моментальный снимок» из системы
. Выполним его «моментальный снимок» из системы  в момент
в момент 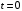 .
.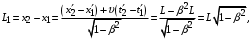 (6)
(6)где:
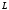 — собственная длина тела, покоящегося в системе
— собственная длина тела, покоящегося в системе  , м;
, м;  — промежуток времени, разделяющий два события в системе
— промежуток времени, разделяющий два события в системе  , с;
, с;  ,
,  и
и  ,
,  — пространственно-временные координаты в системе
— пространственно-временные координаты в системе  и
и  соответственно, м, с; υ — скорость движения системы
соответственно, м, с; υ — скорость движения системы  относительно
относительно  вдоль оси
вдоль оси  , м/с;
, м/с;  — скорость света, м/с;
— скорость света, м/с;  .
.3. 4. Скорость материальной точки в разных системах отсчёта:
Пусть материальная точка равномерно движется в системе
 со скоростью
со скоростью  в направлении оси
в направлении оси  ;
; 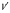 – скорость этой материальной точки в системе
– скорость этой материальной точки в системе  . Так как
. Так как 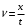 и
и 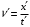 , то:
, то:
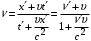 , (7)
, (7)где:
 — время движения, с;
— время движения, с; 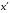 — координата в системе
— координата в системе  , м; υ — скорость движения, м/с;
, м; υ — скорость движения, м/с;  — скорость материальной точки в системе
— скорость материальной точки в системе  , м/с;
, м/с;  — скорость света, м/с.
— скорость света, м/с.Так выражается скорость материальной точки в одной системе отсчёта через её скорость в другой системе.
4. Релятивистская динамика
4.1 Основной закон релятивистской динамики
Основной закон релятивистской динамики: скорость изменения импульса материальной точки равна силе
 , действующей на эту точку, т. е.
, действующей на эту точку, т. е.
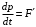 , или
, или 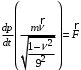 (8)
(8)Примечание. Если на материальную точку одновременно действует несколько сил, то под силой
 нужно понимать равнодействующую силу.
нужно понимать равнодействующую силу. Элементарная работа силы
 на малом перемещении
на малом перемещении 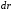 точки её приложения равна
точки её приложения равна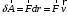 (9)
(9)Из основного закона релятивистской динамики следует, что элементарная работа силы
 , действующей на материальную точку массы
, действующей на материальную точку массы 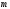 равна
равна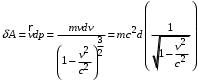 (10)
(10)4. 2. Релятивистская масса:
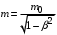 , (11)
, (11)где
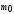 — масса покоя, кг;
— масса покоя, кг; 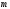 – релятивистская масса, кг;
– релятивистская масса, кг;  .
.
Масса частицы (инвариантная масса) не зависит от скорости, являясь инвариантом относительно преобразований Лоренца, и является величиной неаддитивной. В данной формуле речь идет о релятивистской массе, которая возрастает с увеличением скорости.
4. 3. Связь энергии и массы материальной точки:
Энергией покоя
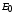 материальная точка обладает в ИСО относительно которой она покоится и называется собственной энергией материальной точки:
материальная точка обладает в ИСО относительно которой она покоится и называется собственной энергией материальной точки: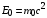 , (12)
, (12)где:
 — масса покоя материальной точки, кг;
— масса покоя материальной точки, кг;  — скорость света, м/с.
— скорость света, м/с.Любое изменение энергии материальной точки означает изменение её массы и наоборот:
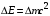 , (13)
, (13)где:
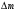 — изменение массы материальной точки, кг;
— изменение массы материальной точки, кг;  — скорость света, м/с.
— скорость света, м/с.Полная энергия материальной точки:
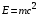 , (14)
, (14)где:
 — масса материальной точки, кг;
— масса материальной точки, кг;  — скорость света, м/с.
— скорость света, м/с. Между полной энергией материальной точки, энергией покоя и импульсом существует зависимость:
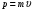 (15)
(15) значит: (16)
значит: (16)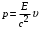 составим: (17)
составим: (17)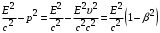 (18)
(18)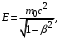 запишем: (19)
запишем: (19)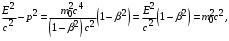 (20)
(20)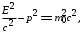 (21)
(21)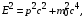 тогда: (22)
тогда: (22)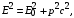 (23)
(23)
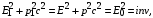 (24)
(24)где:
 — энергия покоя, Дж; p — импульс, кг.м/с;
— энергия покоя, Дж; p — импульс, кг.м/с;  — скорость света, м/с;
— скорость света, м/с;  — масса материальной точки, кг;
— масса материальной точки, кг; 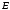 — полная энергия, Дж;
— полная энергия, Дж;  — масса покоя, кг;
— масса покоя, кг;  .
.Рассмотрим задачу:
Какую скорость должно иметь тело в виде куба со сторонами а при движении вдоль оси х, как показано на рисунке 1, чтобы плотность тела увеличилась в два раза? Ответ представить в мегаметрах за секунду и округлить до целого числа.
Решение:
По определению плотность — скалярная физическая величина, определяемая как отношение массы тела к занимаемому этим телом объёму, значит:
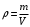 , (1)
, (1)где:
 — масса тела, кг;
— масса тела, кг; 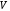 — объём тела, м3.
— объём тела, м3. 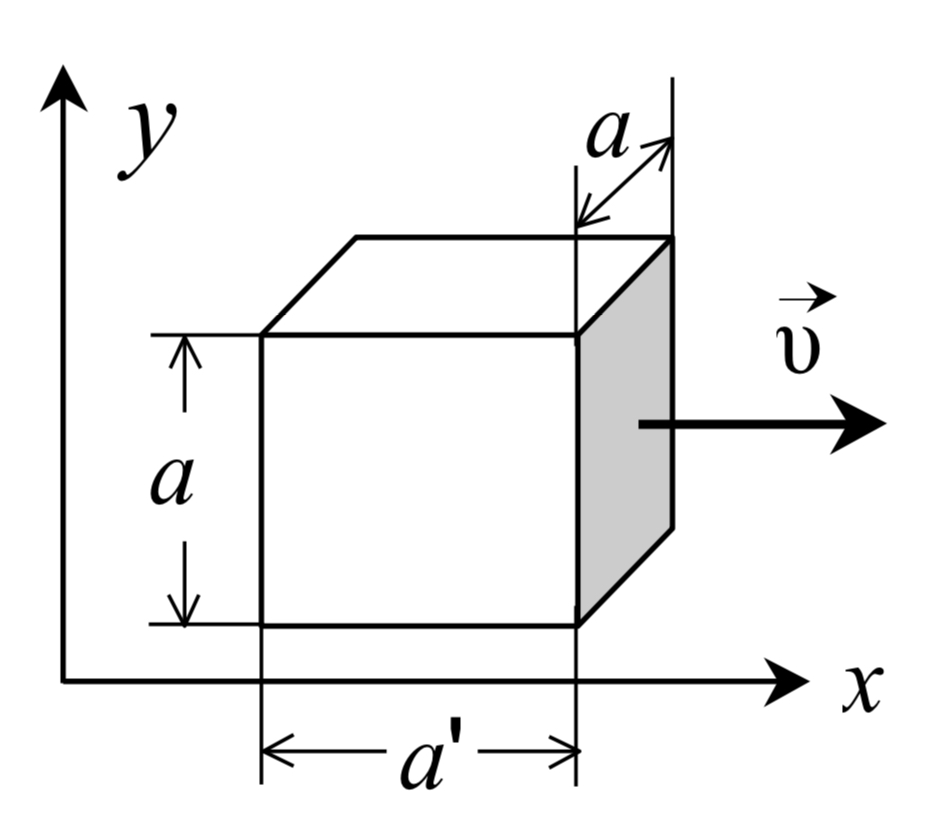
Рисунок 1 — Тело в виде куба со сторонами a движется по направлению вдоль оси x со скоростью υ.
По условию задачи плотность тела должна увеличится в 2 раза, значит
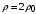 .
. Выражение (1) примет вид:
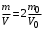 (2)
(2)где:
 — масса движущегося куба, кг;
— масса движущегося куба, кг;  — масса куба в состоянии покоя, кг;
— масса куба в состоянии покоя, кг; 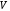 — объём движущегося куба, м3;
— объём движущегося куба, м3; 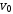 — объём куба в состоянии покоя, м3.
— объём куба в состоянии покоя, м3. При скоростях близких к скорости света масса тела увеличивается, становясь бесконечно большой при υ = c:
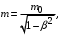 (3)
(3)где:
 — масса куба в состоянии покоя, кг;
— масса куба в состоянии покоя, кг;  .
.
