Файл: Основные понятия теории моделирования и анализа информационных процессов (1 час).docx

Отчет о работе

Отчет должен содержать:

1) задание и исходные данные по заданному варианту лабораторной работы;

2) краткое описание используемых технических и программных средств;

3) обоснование выбора конкретных статистических объектов GPSS для реализации данного варианта задания;

4) обоснование принимаемых решений;

5) блок–диаграмму GPSS и описание результирующей программы;

6) текст результирующей программы и окончательные результаты решения поставленной задачи моделирования.

Лабораторное занятие № 11

Тема: «Функция распределения вероятностей случайной величины. (интегральная функция распределения)» (2 часа)

Задание к работе

1. Конкретизировать свойства интегральной функции распределения

2. Найти интегральную функцию распределения F(x) и начертить ее график.
Результат любого случайного эксперимента можно характеризовать качественно и количественно. Качественный результат случайного эксперимента - случайное событие. Любая количественная характеристика, которая в результате случайного эксперимента может принять одно из некоторого множества значений, - случайная величина. Случайная величинаявляется одним из центральных понятий теории вероятностей.

Пусть  - произвольное вероятностное пространство. Случайной величиной называется действительная числовая функция x =x (w ), w   W , такая, что при любом действительном x  .

Событие  принято записывать в виде x < x. В дальнейшем случайные величины будем обозначать строчными греческими буквами x , h , z , …

Случайной величиной является число очков, выпавших при бросании игральной кости, или рост случайно выбранного из учебной группы студента. В первом случае мы имеем дело с дискретной случайной величиной (она принимает значения из дискретного числового множества M=

---

{1, 2, 3, 4, 5, 6} ; во втором случае - с непрерывной случайной величиной (она принимает значения из непрерывного числового множества - из промежутка числовой прямой I=[100, 3000]).

Функция распределения случайной величины. Её свойства

Каждая случайная величина полностью определяется своей функцией распределения.

Если x .- случайная величина, то функция F(x) = F_x(x) = P(x < x) называется функцией распределения случайной величины x . Здесь P(x < x) - вероятность того, что случайная величина x принимает значение, меньшее x.

Важно понимать, что функция распределения является “паспортом” случайной величины: она содержит всю информация о случайной величине и поэтому изучение случайной величины заключается в исследовании ее функции распределения, которую часто называют просто распределением.

Функция распределения любой случайной величины обладает следующими свойствами:

• 
  F(x)определена на всей числовой прямой R;
  
• 
  F(x)не убывает, т.е. если x₁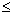 x₂, то F(x₁) 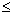 F(x₂);
  
• 
  F(-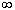 )=0, F(+ 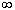)=1,т.е.  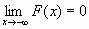 и  ;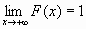
  
• 
  F(x) непрерывна справа, т.е.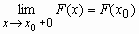 
  

.

Функция распределения дискретной случайной величины

Если x - дискретная случайная величина, принимающая значения x₁ < x₂ < … < x_i < … с вероятностями p₁ < p₂ < … < p_i < …, то таблица вида

x1	x2	…	xi	…
p1	p2	…	pi	…

---

называется распределением дискретной случайной величины.

Функция распределения случайной величины, с таким распределением, имеет вид



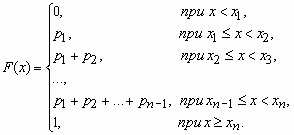
У дискретной случайной величины функция распределения ступенчатая. Например, для случайного числа очков, выпавших при одном бросании игральной кости, распределение, функция распределения и график функции распределения имеют вид:

1	2	3	4	5	6
1/6	1/6	1/6	1/6	1/6	1/6

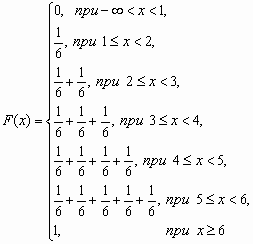
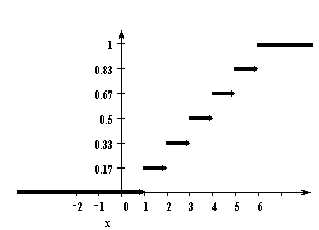
Функция распределения и плотность вероятности непрерывной случайной величины

Если функция распределения F_x(x) непрерывна, то случайная величина x называется непрерывной случайной величиной.

Если функция распределения непрерывной случайной величины дифференцируема, то более наглядное представление о случайной величине дает плотность вероятности случайной величины p_x(x), которая связана с функцией распределения F_x(x) формулам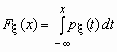и

 и  .

Отсюда, в частности, следует, что для любой случайной величины  .

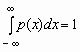Квантили

При решении практических задач часто требуется найти значение x, при котором функция распределения F_x(x) случайной величины x принимает заданное значение p, т.е. требуется решить уравнение F_x(x) = p. Решения такого уравнения (соответствующие значения x) в теории вероятностей называются квантилями.

Квантилью x_p (p-квантилью, квантилью уровня p) случайной величины 

---

, имеющей функцию распределения F_x(x), называют решение x_pуравнения F_x(x) = p, p   (0, 1). Для некоторых p уравнение F_x(x) = p может иметь несколько решений, для некоторых - ни одного. Это означает, что для соответствующей случайной величины некоторые квантили определены неоднозначно, а некоторые кванитили не существуют.

Квантили, наиболее часто встречающиеся в практических задачах, имеют свои названия:

медиана - квантиль уровня0.5;

нижняя квартиль - квантиль уровня0.25;

верхняя квартиль - квантиль уровня0.75;

децили - квантили уровней0.1, 0.2, …, 0.9;

процентили - квантили уровней 0.01, 0.02, …, 0.99.

Вероятность попадания в интервал

Вероятность того, что значение случайной величины F_x(x) попадает в интервал (a, b), равная P(a < x < b) = F_x(b) -F_x(a), вычисляется по формулам:

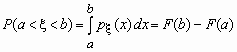 - для непрерывной случайной величины и

- для дискретной случайной величины.

Если a= -  , то   ,

если b=  , то  .

Лабораторное занятие № 12 (2 часа)

«Моделирование управление запасами «Поставщик-склад-потребитель» Цель работы: Выполнить моделировании управление запасами «Поставщик-склад-потребитель»

Задания:

1. 
   Изучить и провести анализ складских операций на предприятии
   
2. 
   Выполнить моделирование по управлению запасами «Поставщик-склад-потребитель»
   
3. 
   Решение задач
   

1. Модель с фиксированным (оптимальным) размером заказа

Эта модель предусматривает постоянный контроль уровня запасов. Заказ на пополнение запаса имеет фиксированный объем и формируется всякий раз, когда уровень запасов снижается до так называемой «точки заказа». Уровень «точки заказа» включает предполагаемый объем потребления рассматриваемого МТР за время реализации заказа и страховой запас, необходимый для обеспечения требуемого уровня надежности снабжения данным МТР при возможных колебаниях уровня спроса и времени реализации заказа.

---

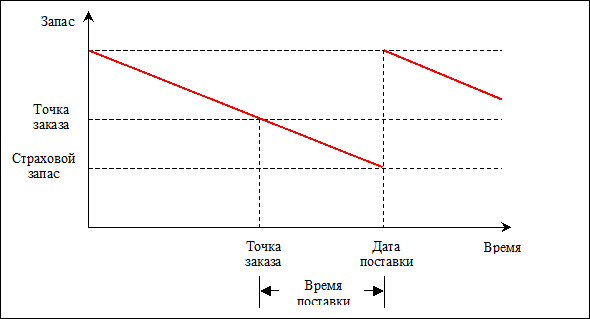
Величина партии заказа должна минимизировать суммарные расходы на пополнение и хранение запаса при заданных условиях поставок (т.е. с учетом  величины минимальной партии заказа, периодичности поставок, системы скидок и т.д.).

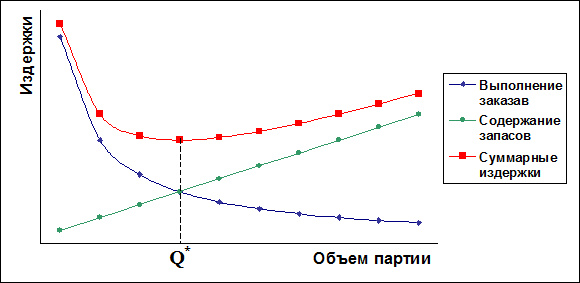
Для решения задачи оптимизации необходимо составить целевую функцию затрат, выражающую зависимость удельных затрат на пополнение и хранение запасов от объема поставки (Q), а затем найти значение аргумента Q, при котором целевая функция достигает своего наименьшего значения.

При формировании целевой функции в нее нет смысла включать величины, не зависящие от объема партии заказа. По этой причине из совокупных расходов на приобретение и хранение запасов, в частности, исключаются:

• 
  стоимость закупаемого МТР, если цена на него не зависит от объема партии (поскольку - независимо от объема партии заказа - совокупный объем закупок за весь период планирования определяется объемом спроса);
  
• 
  стоимость хранения страхового запаса, если его уровень поддерживается постоянным.
  

В простейшем случае (при постоянном спросе и при отсутствии ограничений, вытекающих из условий поставок) целевая функция имеет вид:

С(Q) = с_зк×d/Q + с_хр×Q/2 ,                                                     (1)

и достигает наименьшего значения в точке

                                                      (2)

Формула (2) называется формулой оптимальной партии заказа (или формулой Уилсона) [3].



«Точка заказа» определяется по формуле:

s = d×L + q_стр ,                                                                       (3)

а максимальный уровень запаса - по формуле:

S = s + Q^* .                                                                (4)

Как видно из (4), максимальный уровень запаса включает как собственно складской запас, так и заказанную партию и достигается в момент начала поставки; фактический же уровень складского запаса после завершения поставки будет, естественно, несколько ниже. Аналогичное замечание справедливо и в отношении «точки заказа»: если время выполнения заказа столь велико, что необходимость очередного пополнения запасов может возникнуть еще до прибытия предыдущей партии, то при практическом применении критерия «точки заказа» следует учитывать все наличные запасы, включая «запасы в пути».

---