Файл: Вариант 7 н айти область определения функции и изобразить её на плоскости Д ля заданной функции область определяется следующим неравенством, или..doc
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 03.02.2024
Просмотров: 17
Скачиваний: 0
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Вариант № 7
-
Н
айти область определения функции и изобразить её на плоскости: 
.
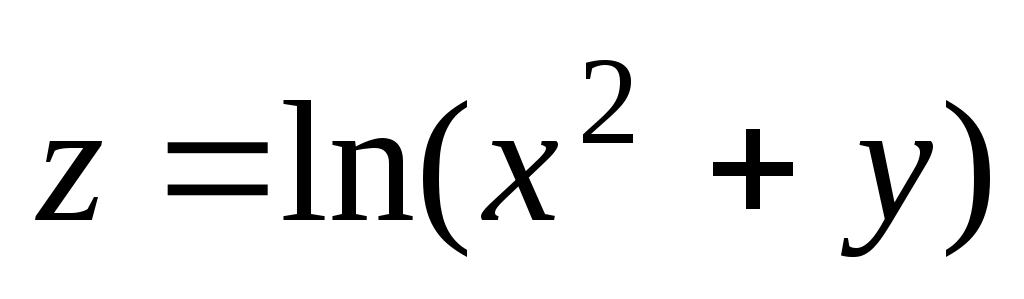Д
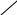
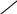
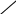
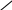
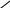ля заданной функции область определяется следующим неравенством: 
, или
. Это неравенство определяет область, расположенную выше линии параболы 
, причём сама линия параболы не входит в указанную область (см. рисунок). Ответ:
. -
Вычислить частные производные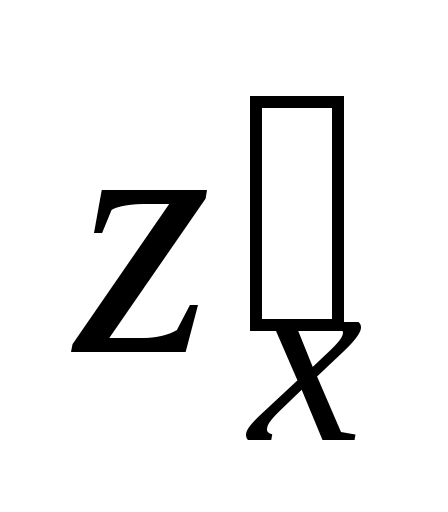
и 
сложной функции в данной точке: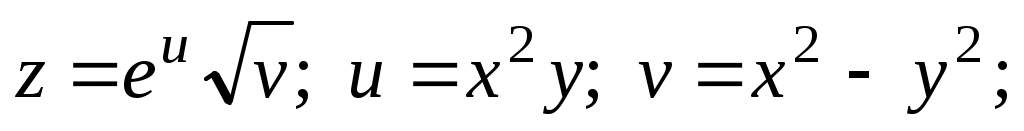 
при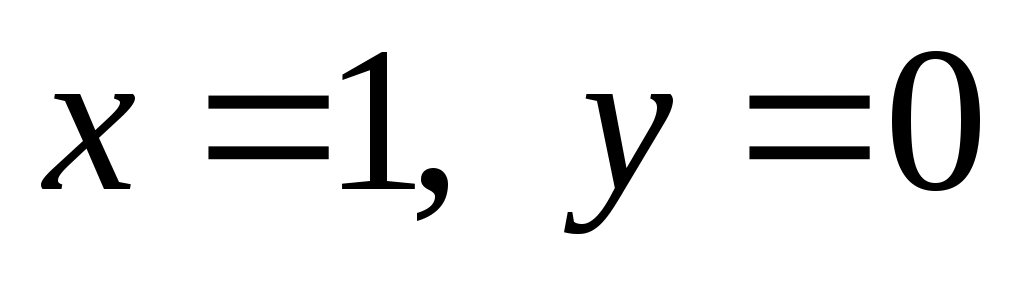 
.
Частные производные сложной функции двух переменных
находятся по формулам 
и 
. В данном случае 
. Следовательно, 
, 
. Заметим, что в точке 
промежуточные переменные равны: 
. Подставляя в частные производные 
, получим: 
, 
. Ответ: 
, 
.-
Найти уравнение касательной плоскости и нормали к указанной поверхности в данной на ней точке: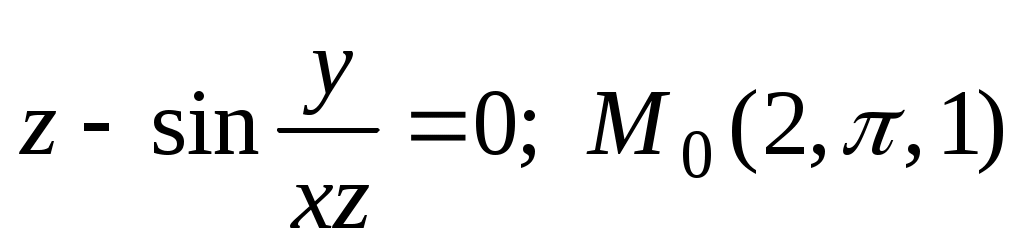
.
Касательная плоскость и нормаль к поверхности
в точке
имеют следующие уравнения: а) 
(касательная плоскость): 
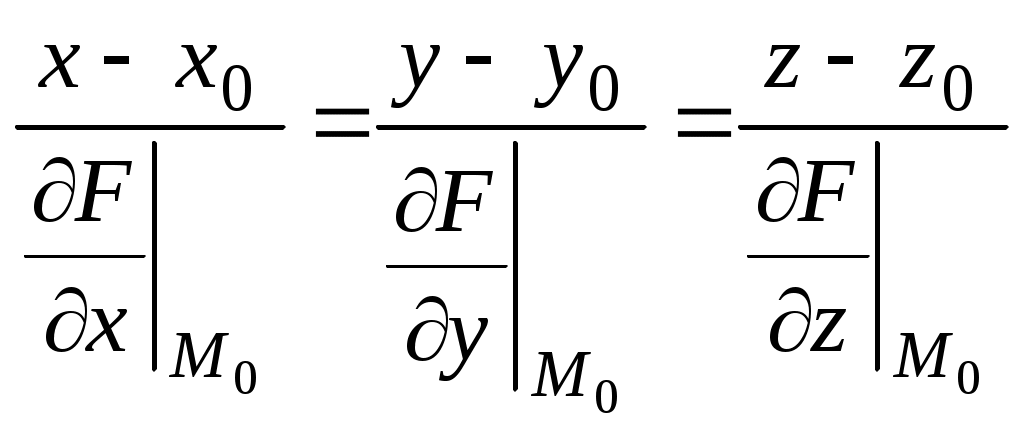(нормаль). В данном случае 
. Найдём частные производные от 
в точке 
: 
. Подставим найденные частные производные в уравнения касательной плоскости и нормали: 
, 
. Ответ: а) Уравнение касательной плоскости: ; б) Уравнение нормали: .-
Найти наибольшее и наименьшее значения функции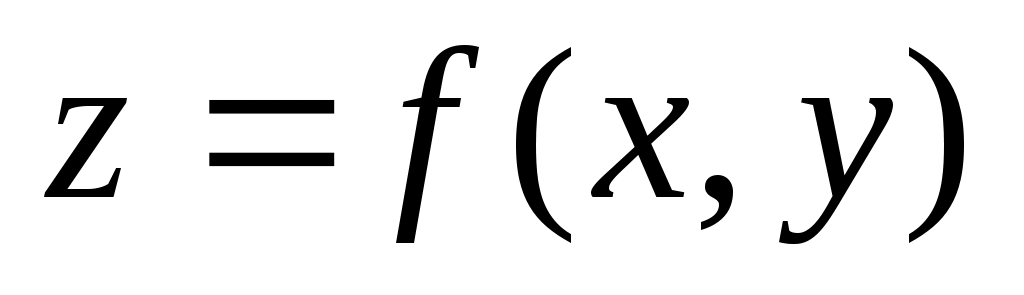
в области D: 
.
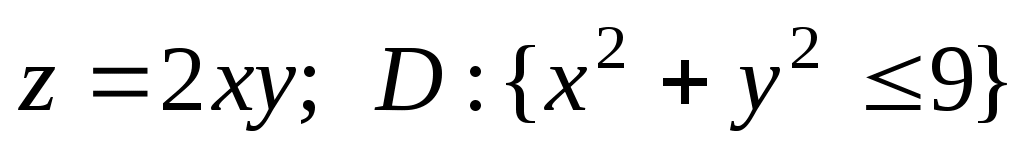С
тационарная точка 
не является точкой экстремума, поскольку функция является возрастающей функцией своих аргументов. На границе области D 
, 
, функция имеет вид 
. Тогда 
. Приравнивая производную к нулю, получим четыре стационарные точки 
. Стационарные точки
расположены в верхней полуокружности, т.е. 
, точки 
- в нижней части, т.е. 
. В этих точках функция соответственно равна: 
. Сравнивая эти значения, видим, что наибольшее значение 
функция принимает в точках 
, а наименьшее значение 
- в точках 
. Ответ: наибольшее значение функции - в точках , наименьшее значение - в точках .-
Изменить порядок интегрирования: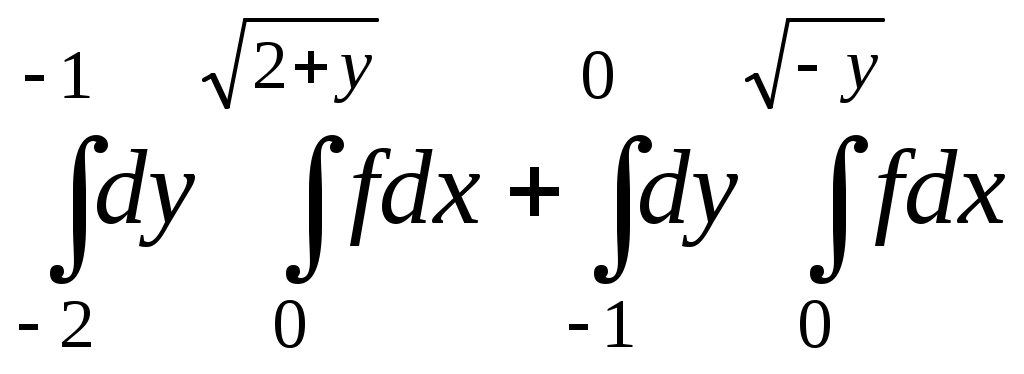
.
В
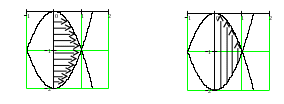
осстановим область интегрирования (D) по пределам повторных интегралов:
, 
. Изобразим область интегрирования на чертеже (см. рисунок). Найдём точки пересечения парабол 
и 
: 
. Порядок интегрирования в данном интеграле показан штриховкой на первом графике. На втором графике штриховка изменена на вертикальную. Из рисунка видим, что данная область является y – трапецией. На нижней границе
, на верхней границе 
. Поэтому 
и в результате подстановки пределов получим следующий повторный интеграл: 
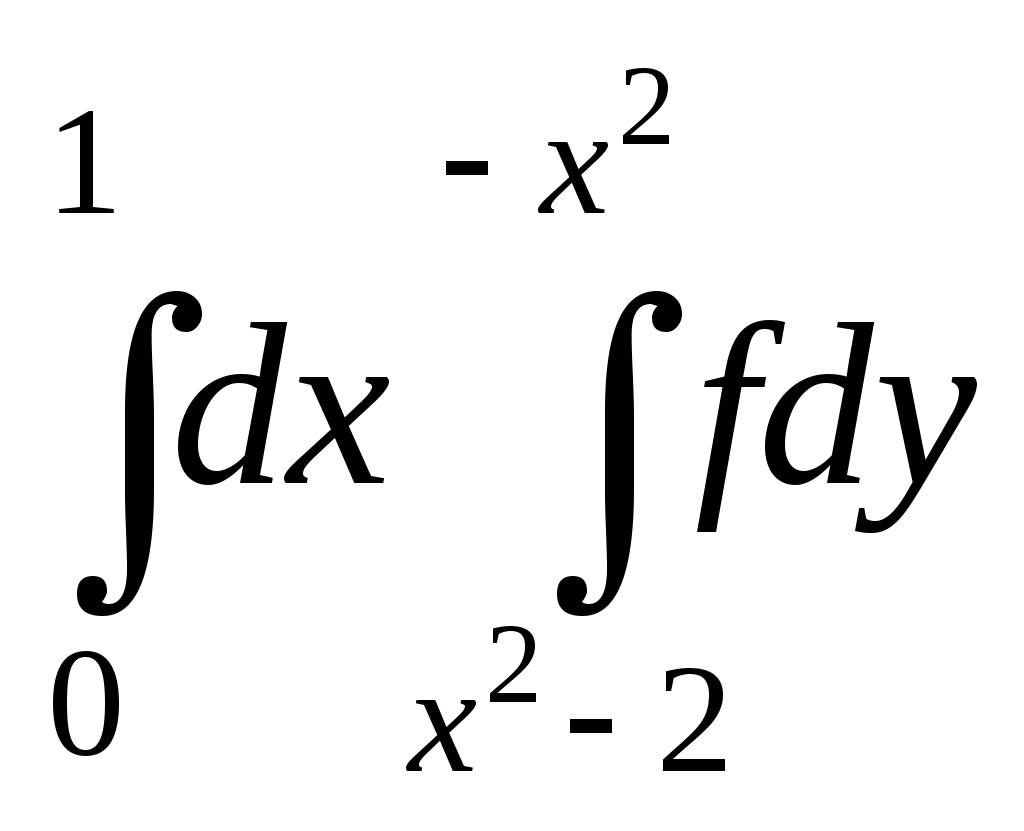. Ответ: .-
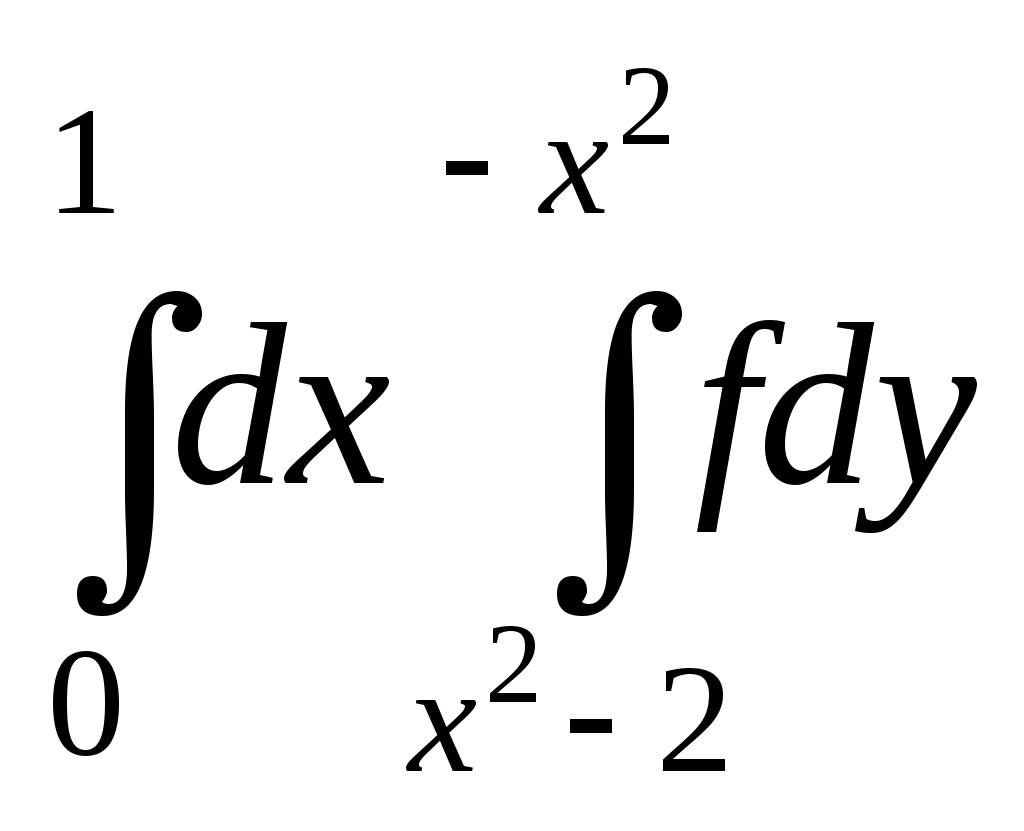Н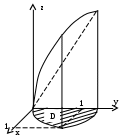
айти объём тела, ограниченного указанными поверхностями: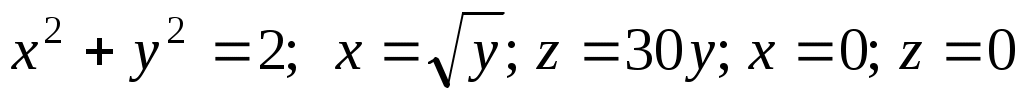
.
Основанием тела в плоскости ХОУ является область D, ограниченная параболой
и окружностью 
, которые пересекаются в точке 
. Снизу тело ограничено плоскостью 
, сверху – плоскостью 
(см. рисунок). Таким образом,
. Ответ: 
.-
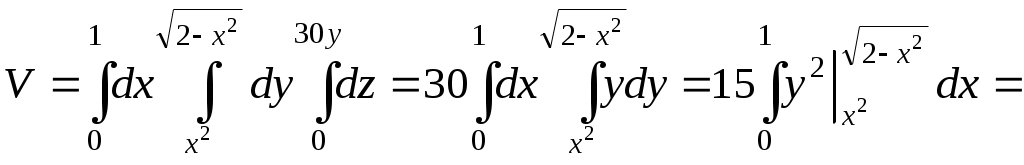
Н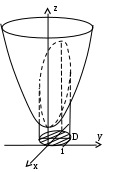
айти объём тела, ограниченного указанными поверхностями: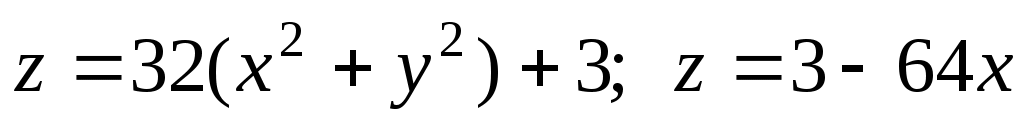
.
Параболоид вращения
ограничен сверху плоскостью 
(см. рисунок). Проекция тела на плоскость ХОУ представляет круг 
. Сверху тело ограничено плоскостью, а снизу – поверхностью параболоида. Удобно перейти к цилиндрическим координатам: