Файл: Вариант 7 н айти область определения функции и изобразить её на плоскости Д ля заданной функции область определяется следующим неравенством, или..doc
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 03.02.2024
Просмотров: 19
Скачиваний: 0
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
-
Найти объём тела, ограниченного указанными поверхностями: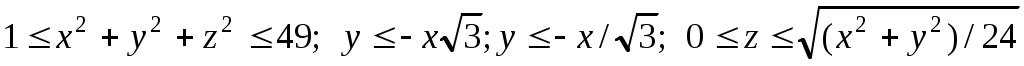 .
.
Т
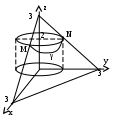
 ело расположено между двумя концентрическими сферами с центрами в начале координат радиуса 1 и 7, конусом (сверху), и двумя плоскостями
ело расположено между двумя концентрическими сферами с центрами в начале координат радиуса 1 и 7, конусом (сверху), и двумя плоскостями -
Найти массу пластинки: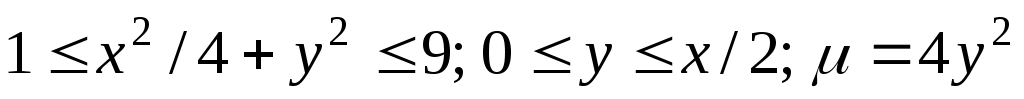
Пластинка занимает область D, и
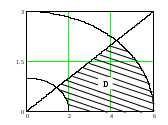
зображённую на рисунке. Область неудобна для интегрирования в декартовой системе координат. Поэтому перейдём к эллиптической системе координат:
-
Найти массу тела: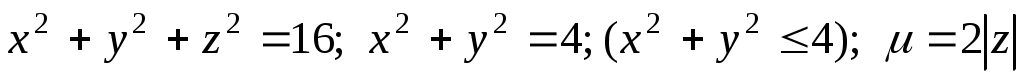 .
.
Т
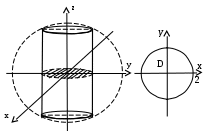
ело представляет часть шара, «вырезанную» цилиндрической поверхностью
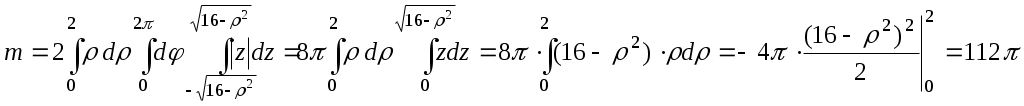 . Ответ:
. Ответ: -


R
Вычислить криволинейный интеграл по формуле Грина: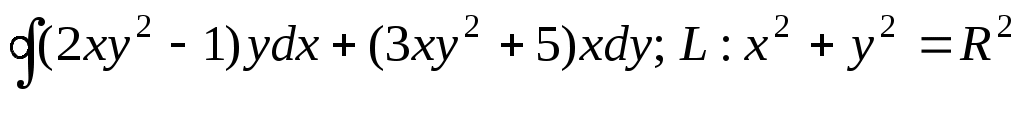 .
.
П
D
реобразуем криволинейный интеграл по замкнутому контуру в двойной по формуле Грина:
Ответ:
.
-
Вычислить массу дуги кривой (L) при заданной плотности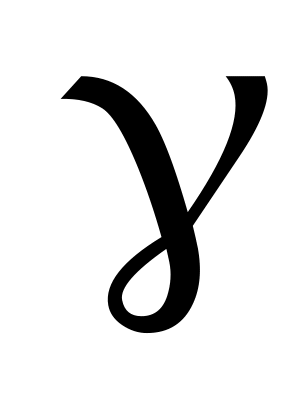 :
:
М
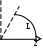
ассу дуги вычисляем с помощью криволинейного интеграла первого рода:
-
Вычислить работу силы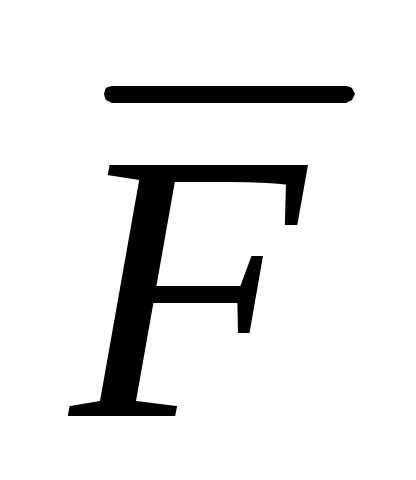 при перемещении вдоль линии
при перемещении вдоль линии 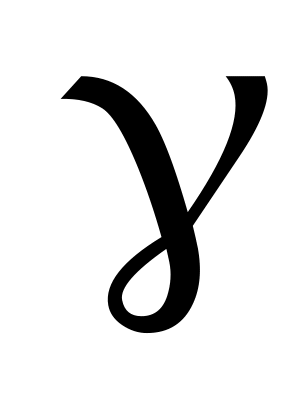 от точки M к точке N:
от точки M к точке N: 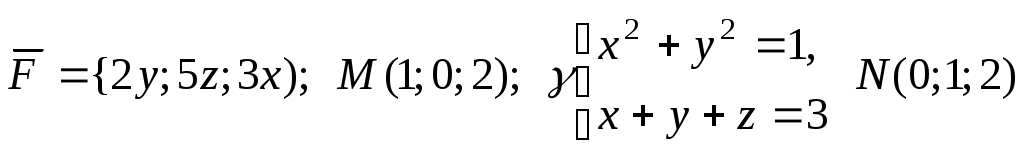 .
.
Работу вычисляем по формуле:
Ответ: Работа равна
-
Найти производную функции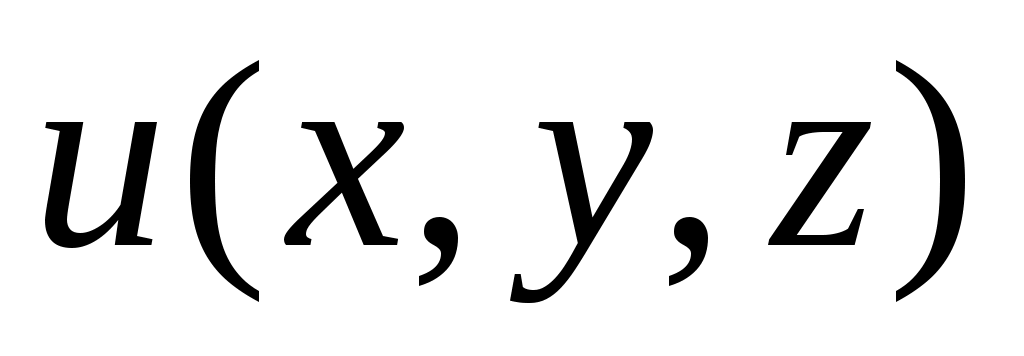 в точке
в точке 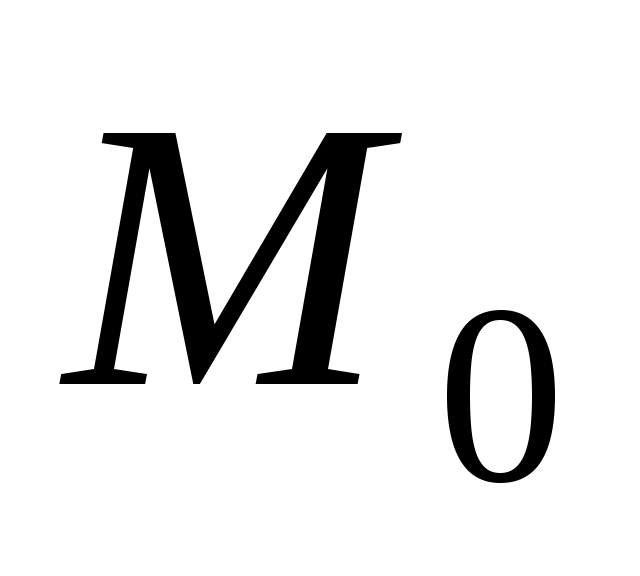 по направлению внешней нормали
по направлению внешней нормали 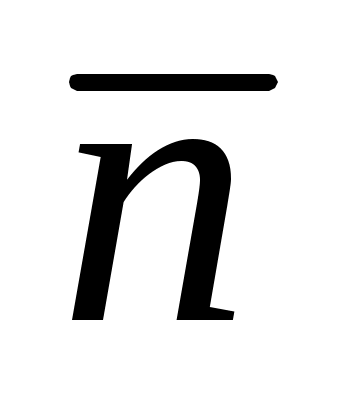 к поверхности
к поверхности 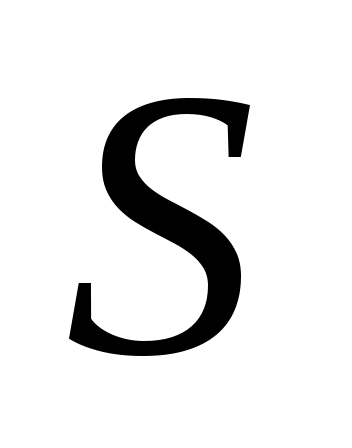 , заданной уравнением
, заданной уравнением 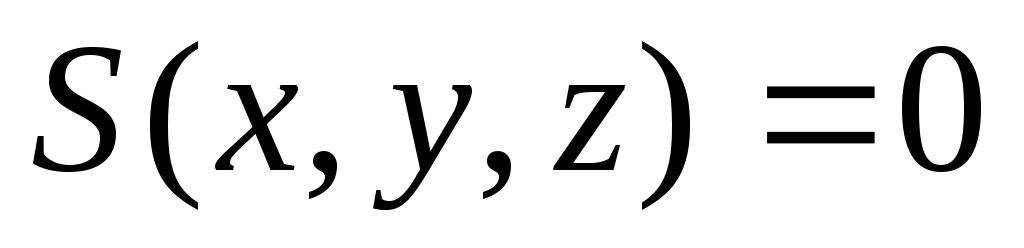 , или по направлению вектора
, или по направлению вектора 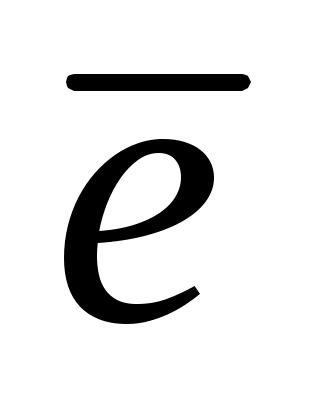 :
: 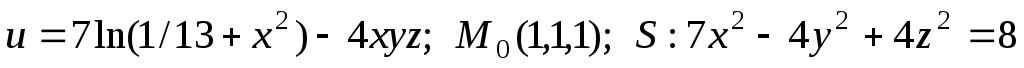 .
.
Производная по направлению находится по формуле:
 Следовательно,
Следовательно, 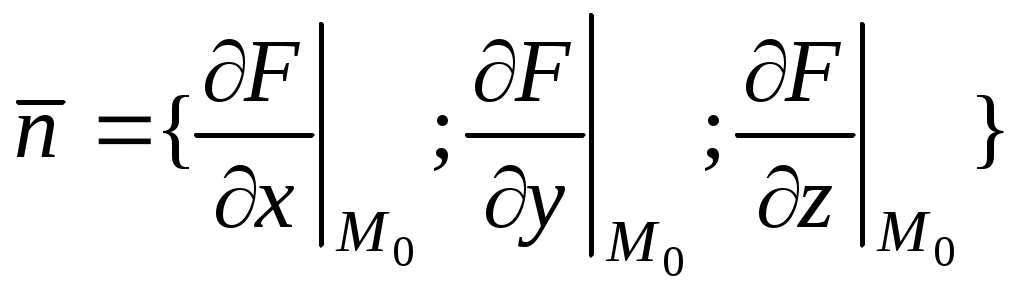 , где
, где
