1)Температурное поле. Температурный градиент. Тепловой поток. Плотность теплового потока. Закон Фурье.

Температурным полем называют совокупность мгновенных значений температуры во всех точках рассматриваемого пространства.

Градиент температуры. Производная температуры по нормали к изотермической поверхности называется градиентом температуры:

Тепловой поток – это поток энергии (в форме теплоты), обусловленный ее самопроизвольным, необратимым переносом в пространстве от более нагретых тел (участков тела) к менее нагретым.

Плотность теплового потока:



Закон Фурье



2)Коэффициент теплопроводности. Условия однозначности для процессов теплопроводности.

Коэффициент теплопроводности– это физический параметр вещества, который в общем случае зависит от температуры, давления и природы вещества.


3)Передача теплоты через однослойную плоскую стенку при граничных условиях I и III рода (теплопередача).

Граничные условия первого рода, в которых задается распределение температуры на поверхности тела для каждого момента времени: tc = f(x, y, z, ); частный случай tc = const

Граничные условия третьего рода, в которых задается температура окружающей среды tж и закон теплообмена между поверхностью тела и окружающей средой в процессе охлаждения и нагревания. Для его описания используется закон Ньютона – Рихмана: плотность теплового потока пропорциональна разности температур поверхности тела tc и окружающей среды tж: q =  (tc – tж). Здесь  – коэффициент теплоотдачи

---

, характеризующий интенсивность теплообмена между поверхностью тела и окружающей средой. Численно равен количеству тепла, отдаваемому (воспринимаемому) единицей поверхности в единицу времени при разности температур между поверхностью и средой в один градус.

Теплопередачей называется передача теплоты от горячего теплоносителя к холодному теплоносителю через стенку, разделяющую эти теплоносители.

Примерами теплопередачи являются: передача теплоты от греющей воды нагревательных элементов (отопительных систем) к воздуху помещения; передача теплоты от дымовых газов к воде через стенки кипятильных труб в паровых котлах; передача теплоты от раскаленных газов к охлаждающей воде (жидкости) через стенку цилиндра двигателя внутреннего сгорания; передача теплоты от внутреннего воздуха помещения к наружному воздуху и т. д. При этом ограждающая стенка является проводником теплоты, через которую теплота передается теплопроводностью, а от стенки к окружающей среде конвекцией и излучением. Поэтому процесс теплопередачи является сложным процессом теплообмена.

П 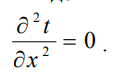ри установившемся, или стационарном, тепловом режиме температура тела не зависит от времени. Рассмотрим однородную и изотропную стенку толщиной  с постоянным коэффициентом теплопроводности . На наружных поверхностях стенки поддерживаются постоянными температуры tc1 и tc2. Дифференциальное уравнение теплопроводности для рассматриваемого случая запишется в виде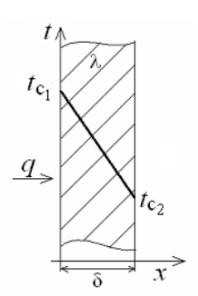

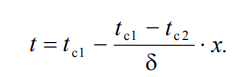Граничные условия в данной задаче зададим следующим образом: при х = 0 t = tc1; при х =  t = tc2. Закон распределения температуры по толщине стенки найдем, дважды проинтегрировав уравнение и найдя константы интегрирования из граничных условий, заданных уравнениями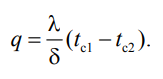

---

Для определения количества тепла, проходящего через единицу поверхности стенки в единицу времени в направлении оси Ох, воспользуемся законом Фурье, согласно которому     / xtq .

Из уравнения следует, что количество тепла, проходящее через единицу поверхности в единицу времени прямо пропорционально коэффициенту теплопроводности и температурному напору и обратно пропорционально толщине стенки. Отношение  / называется тепловой проводимостью стенки, а обратная величина  /  – тепловым или термическим сопротивлением стенки. Последнее представляет собой падение температуры в стенке на единицу плотности теплового потока. Зная удельный тепловой поток, легко вычислить общее количество тепла, которое передается через поверхность стенки величиной F за промежуток времени :

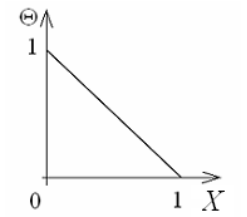
Из уравнения следует, что при прочих равных условиях температура в стенке убывает тем быстрее, чем больше плотность теплового потока. Если отсчет избыточной температуры в стенке вести от наименьшей заданной температуры tc2, то уравнение можно привести к безразмерному виду

Уравнение температурного поля является универсальным, так как распределение температуры в стенке можно представить единой прямой для любых заданных значений температур стенки tc1, tc2 и ее толщины  Выражения и получены в предположении, что коэффициент теплопроводности является постоянной величиной. В действительности это не всегда бывает так. Рассмотрим зависимость коэффициента теплопроводности только от температуры, которая для многих материалов близка к линейной 0   (1 ) bt , где 0 – значение коэффициента теплопроводности при 0о С. Тогда плотность теплового потока на поверхности пластины Из этого уравнения следует, что температура в стенке изменяется не линейно, а по кривой. Характер температурной кривой определяется знаком и численным значением коэффициента b

В опрос 4. Передача теплоты через многослойную плоскую стенку при граничных условиях 1 и 3 рода (теплопередача)

Рассмотрим теплопроводность многослойной стенки состоящей из n однородных слоев. Примем, что контакт между слоями совершенный и температура на соприкасающихся поверхностях двух слоев одинакова. При стационарном режиме тепловой поток, проходящий через любую изотермическую поверхность неоднородной стенки

---

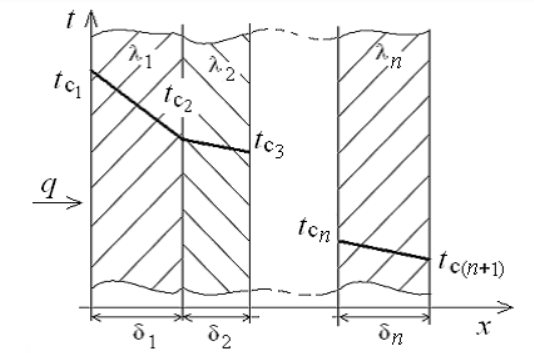
П 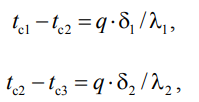ри заданных температурах внешних поверхностей такой стенки, размерах слоев и, соответственно, коэффициентах теплопроводности можно составить систему уравнений для плотности теплового потока каждого из слоев, из которых выразим температурные напоры

О 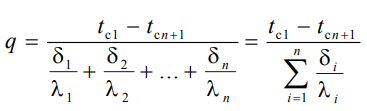тсюда плотность теплового потока



в 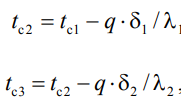еличина , равная сумме тепловых сопротивлений всех n слоев, называется полным тепловым или термическим сопротивлением теплопроводности многослойной стенки. Температуры на границе соприкосновения двух соседних слоев равны

Температуры на границе соприкосновения двух соседних слоев равны

Внутри каждого из слоев температура изменяется согласно уравнениям или для многослойной стенки в целом температурная кривая представляет ломаную линию. При сравнении переноса тепла через многослойную стенку и стенку из однородного материала удобно ввести в рассмотрение эквивалентный коэффициент теплопроводности для многослойной стенки экв. Он равен коэффициенту теплопроводности однородной стенки, толщина которой  равна толщине многослойной стенки , а тепловое сопротивление равно термическому сопротивлению рассматриваемой многослойной стенки, т. е

Т 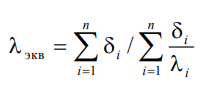аким образом, эквивалентный коэффициент теплопроводности экв зависит не только от теплофизических свойств слоев, но и от их толщины.

П 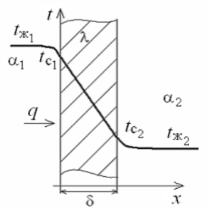ередача тепла от одной жидкой среды (жидкости или газа) к другой через разделяющую их однородную или многослойную твердую стенку любой формы называется теплопередачей. Теплопередача включает в себя теплоотдачу от более горячей жидкости к стенке, теплопроводность в стенке, теплоотдачу от стенки к более холодной подвижной среде

---

Пусть плоская однородная стенка имеет толщину  Заданы коэффициент теплопроводности , температуры окружающей среды tж1 и tж2, а также коэффициенты теплоотдачи 1 и 2. Будем считать, что tж1, tж2, 1 и 2 постоянны и не меняются вдоль поверхности. Это позволяет рассматривать изменение температуры жидкостей и стенки только в направлении, перпендикулярном плоскости стенки. При заданных условиях необходимо найти тепловой поток от горячей жидкости к холодной, а также температуры на поверхностях стенки. Удельный тепловой поток от горячей жидкости к стенке определяется из закона Ньютона – Рихмана уравнением

П ри стационарном тепловом режиме тот же тепловой поток пройдет путем теплопроводности через твердую стенку

Э тот же тепловой поток передается от второй поверхности стенки к холодной жидкости за счет теплоотдачи

А 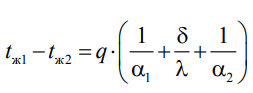налогично решению для многослойной плоской стенки выразим температурные напоры и почленно сложим правые и левые части, тогда

В 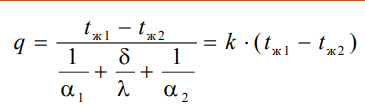ыразим плотность теплового потока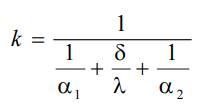



Здесь

коэффициент теплопередачи, характеризующий интенсивность передачи тепла от одной жидкости к другой через разделяющую их стенку, имеет ту же размерность, что и коэффициент теплоотдачи, численно равен количеству тепла, которое передается через единицу поверхности стенки в единицу времени при разности температур между жидкостями в один градус. Величина, обратная коэффициенту теплопередачи, называется полным термическим сопротивлением теплопередачи и для однослойной стенки запишется как



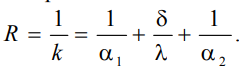
Вопрос 5. Передача теплоты через однослойную цилиндрическую стенку при граничных условиях 1 и 3 рода. Критический диаметр цилиндрической стенки

---

Смотрите также файлы

• Органы чувств.pptx

• Мое отношение к коррупции.docx

• Занятие 1 Обучающийся Кобзева Яна Александровна Преподаватель Губарева Татьяна Викторовна.doc

• Интенсивный курс Матрица, определитель и зачёт!.pdf

• Часть света, западная часть материка Евразия.docx