Р ассмотрим стационарный процесс теплопроводности в бесконечной цилиндрической стенке (трубе) с внутренним диаметром d1 и наружным диаметром d2 с постоянным коэффициентом теплопроводности . На наружных поверхностях трубы поддерживаются постоянными значения температуры tc1 и tc2. Необходимо найти распределение температуры в цилиндрической стенке и тепловой поток через нее. В рассматриваемом случае дифференциальное уравнение теплопроводности удобно записать в цилиндрической системе координат (ось Оz совмещена с осью трубы)

Так как труба бесконечная и изотропная, то дифференциальное уравнение теплопроводности примет вид



у равнение температурного поля в цилиндрической стенке

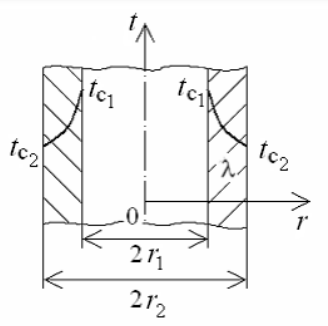
Полученное выражение представляет собой уравнение логарифмической кривой. То обстоятельство, что распределение температуры в цилиндрической стенке является криволинейным, можно объяснить следующим. В случае плоской стенки удельный тепловой поток q остается одинаковым для всех изотермических поверхностей. По этой причине градиент температуры сохраняет для всех изотермических поверхностей постоянную величину. В случае цилиндрической стенки плотность теплового потока через любую изотермическую поверхность будет величиной переменной, так как величина поверхности зависит от радиуса

Д 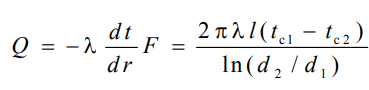ля определения количества теплоты, проходящего через цилиндрическую поверхность величиной F  2  r l в единицу времени, следует воспользоваться законом Фурье



Тепловой поток через единицу внутренней поверхности

Т епловой поток через единицу внешней поверхности

---

Т 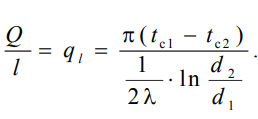епловой поток на единицу длины трубы

Тепловой поток, отнесенный к единице длины трубы, имеет размерность Вт/м и называется линейной плотностью теплового потока

Критический диаметр цилиндрической стенки

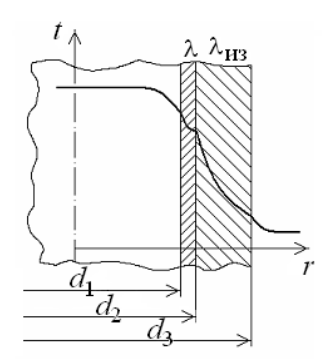
Рассмотрим влияние изменения наружного диаметра d2 на термическое сопротивление однородной цилиндрической стенки. При постоянных значениях 1, 2,  и d1 полное термическое сопротивление теплопередачи цилиндрической стенки будет зависеть только от внешнего диаметра. При этих условиях термическое сопротивление теплоотдачи на внутренней поверхности цилиндра



Термическое сопротивление теплопроводности



термическое сопротивление теплоотдачи на наружной поверхности цилиндра

О чевидно, что полное термическое сопротивление будет определяться характером изменения термических сопротивлений теплопроводности и теплоотдачи от наружной поверхности

З начение внешнего диаметра трубы, соответствующего минимальному полному термическому сопротивлению теплопередачи в цилиндрической стенке, называется критическим диаметром и рассчитывается по формуле

П 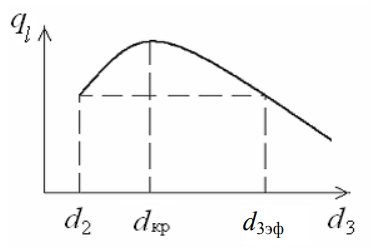ри d2 < dкр с увеличением d2 полное термическое сопротивление теплопередачи падает, так как увеличение наружной поверхности оказывает на термическое сопротивление большее влияние, чем увеличение толщины стенки.

При d2 > dкр с увеличением d2 термическое сопротивление теплопередачи возрастает, что указывает на доминирующее влияние толщины стенки. Изложенные соображения необходимо учитывать при выборе тепловой изоляции различных цилиндрических аппаратов и трубопроводов. Рассмотрим критический диаметр изоляции, наложенной на трубу.

Термическое сопротивление теплопередачи для такой трубы

---

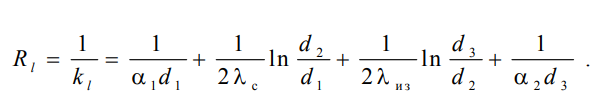
В ыбрав какой-либо теплоизоляционный материал для покрытия цилиндрической поверхности, прежде всего нужно рассчитать критический диаметр изоляции

Е сли окажется, что величина dкр.из больше наружного диаметра трубы d2, то применение выбранного материала в качестве тепловой изоляции в области d2 < d3 < dкр.из приведет к тому, что при увеличении толщины изоляции будет наблюдаться увеличение потерь тепла. Только при d3 = dэф потери тепла вновь станут такими же, как для первоначального, неизолированного трубопровода

Следовательно, некоторый слой тепловой изоляции не будет оправдывать своего назначения. Таким образом, для эффективной работы тепловой изоляции необходимо, чтобы dкр.из  d2

Вопрос 6. Передача теплоты через многослойную цилиндрическую стенку при граничных условиях 1 и 3 рода.

Р 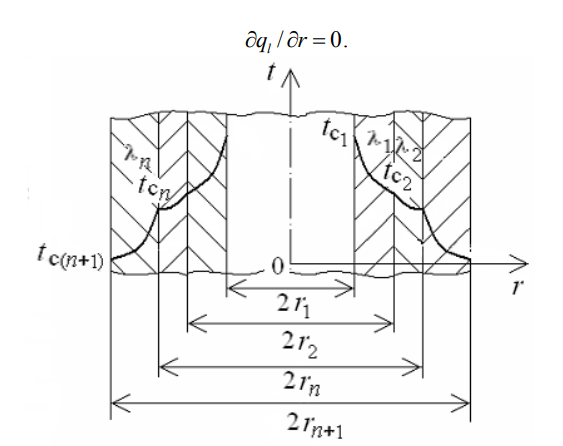ассмотрим теплопроводность многослойной цилиндрической стенки, состоящей из n однородных слоев. Примем, что контакт между слоями совершенный и температура на соприкасающихся поверхностях соседних слоев одинакова. Заданы температуры на внешних поверхностях стенки, коэффициенты теплопроводности и толщины слоев (рис. 4.2). Метод решения аналогичен методу для плоской многослойной стенки. При стационарном тепловом режиме линейная плотность теплового потока не меняется по толщине стенки

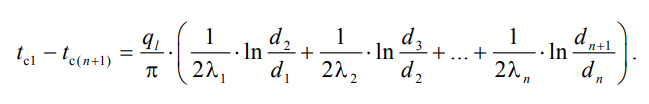Составим систему уравнений линейных плотностей теплового потока для каждого из слоев. Выразим из них температурные напоры и почленно сложим уравнения, тогда

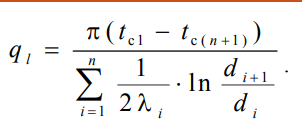Отсюда линейная плотность теплового потока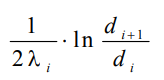



В

---

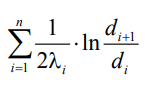
еличина называется линейным термическим сопротивлением теплопроводности отдельного слоя, а величина

п 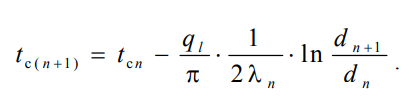редставляет собой термическое сопротивление всех слоев и называется полным линейным термическим сопротивлением теплопроводности многослойной цилиндрической стенки. Температура на границе соприкосновения любых слоев

Внутри любого слоя температура изменяется по логарифмической кривой

П онятие об эквивалентном коэффициенте теплопроводности для цилиндрической стенки принципиально не отличается от такого же понятия для многослойной плоской стенки: термическое сопротивление, вычисленное по эквивалентному коэффициенту теплопроводности, должно равняться сумме термических сопротивлений всех слоев, образующих многослойную цилиндрическую стенку



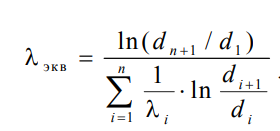
Отсюда эквивалентный коэффициент теплопроводности

Рассмотрим однородную цилиндрическую стенку (трубу) с внутренним диаметром d1 и наружным диаметром d2 с постоянным коэффициентом теплопроводности . Заданы постоянные температуры подвижных сред tж1 и tж2, а также постоянные значения коэффициентов теплоотдачи на внутренней и наружной поверхностях трубы 1 и 2. Необходимо найти температуры поверхностей цилиндрической стенки tс1 и tс2 и тепловой поток через нее

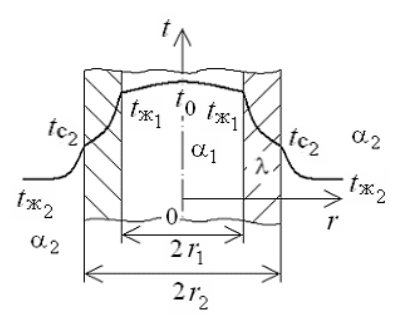
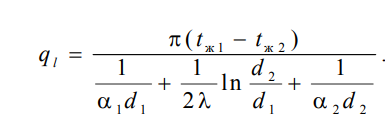Тогда линейная плотность теплового потока определяется как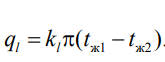



Величина k называется линейным коэффициентом теплопередачи. Она характеризует интенсивность передачи тепла от одной подвижной среды к другой через разделяющую их стенку. Значение k численно равно количеству тепла, которое проходит через стенку трубы длиной один метр в единицу времени от одной жидкой среды к другой при разности температур между ними в один градус. Величина Rl  /1 kR , обратная коэффициенту теплопередачи, называется линейным термическим сопротивлением теплопередачи:

---

В 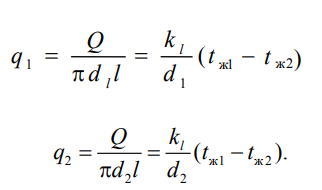отличие от термических сопротивлений теплоотдачи для плоской стенки здесь термические сопротивления теплоотдачи зависят не только от коэффициента теплоотдачи, но и от диаметра стенки. Если тепловой поток через цилиндрическую стенку отнести к внутренней или наружной поверхности стенки, то получим плотность теплового потока, отнесенную к единице соответствующей поверхности трубы

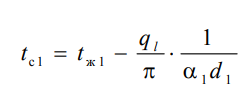
Т 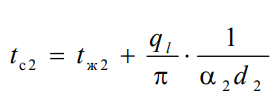емпературы поверхностей цилиндра

В случае теплопередачи через многослойную цилиндрическую стенку линейная плотность теплового потока определяется как

В 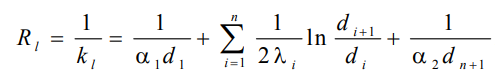еличина Rl называется полным термическим сопротивлением теплопередачи многослойной цилиндрической стенки и равна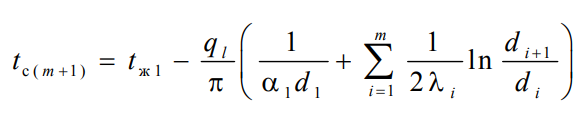



Температуры стенок

Вопрос 7. Теплопроводность при наличии внутренних источников теплоты (однородная пластина)

В одномерном случае (примером является плоская пластина, толщина которой много меньше двух других ее размеров) дифференциальное уравнение теплопроводности упрощается и в декартовой системе координат имеет вид

П 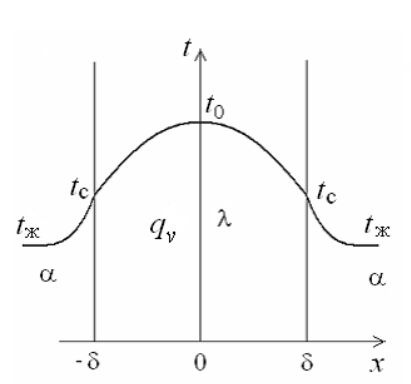остоянные интегрирования определяются в зависимости от условий охлаждения на поверхности пластины.

Рассмотрим длинную пластину, толщина которой 2 – величина малая по сравнению с двумя другими размерами Источники равномерно распределены по всему объему и равны qv = const. Заданы постоянные коэффициенты теплоотдачи  = = const и температура жидкости вдали от пластины tж = const. Благодаря симметричному отводу теплоты температуры обеих поверхностей пластины одинаковы. При указанных условиях температура пластины будет изменяться только вдоль оси х, направленной нормально к поверхности тела

---

Смотрите также файлы

• Органы чувств.pptx

• Мое отношение к коррупции.docx

• Занятие 1 Обучающийся Кобзева Яна Александровна Преподаватель Губарева Татьяна Викторовна.doc

• Интенсивный курс Матрица, определитель и зачёт!.pdf

• Часть света, западная часть материка Евразия.docx