ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 02.02.2024
Просмотров: 72
Скачиваний: 0
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Угловое ускорение направлено на нас, то есть направлено в противоположенную сторону относительно угловой скорости, поскольку движение – замедленное.
Напоследок, приведем важные формулы кинематики, вывод которых и глубокое раскрытие физического смысла в нашем курсе не предусмотрено.
Линейная скорость связана с угловой через радиус траектории:
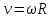
Предположим, что скорость предмета изменяется по величине. Из этого следует, что угловая скорость также будет изменяться по величине. Тогда справедливо записать:
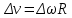
Тангенциальное ускорение есть:
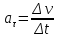
Угловое ускорение есть:
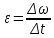
Тогда:
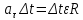
Окончательно получим взаимосвязь тангенциального и углового ускорений:
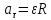
Время, которое требуется предмету для совершения полного оборота по окружности, называется периодом обращения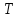
.
Если предмет совершает полный оборот вдоль окружности, следовательно, он поворачивается на угол, равный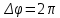
. Если предмет движется с постоянной угловой скоростью, то справедливо равенство:
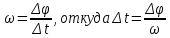
Откуда, получим формулу периода обращения, с учетом, что :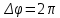
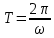
Угловую скорость часто называют угловой частотой. Однако, на практике оказывается полезным пользоваться и линейной частотой, которую обозначают буквой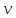
. Линейная частота связана с угловой как:
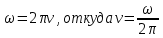
Используя формулу для периода обращения, получим:
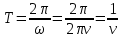
Линейная частота равна числу событий, совершаемых в единицу времени (в секунду). Измеряется она в Герцах [Гц]. Например, лампочка мигает 4 раза в секунду, тогда линейная частота мигания лампочки равна 4 Гц.
Свяжем период обращения с линейной скоростью:
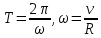
Тогда:
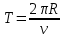
Приведем еще один пример, который было бы неудобно привести в ходе основного повествования. Ранее, по заданному уравнению координаты от времени, мы определяли величину скорости (делали это для линейной функции и искали тангенс угла наклона функции к горизонтальной оси, который численно равен скорости). Однако, существует обратная задача – когда по функции уравнения скорости, зависящей от времени, необходимо определить путь или перемещения, пройденные предметом.
Пример 12.
На графике представлена проекция скорости материальной точки на ось x в зависимости от времени. В начальный момент времени материальная точка находилась в начале координат. Определить ее среднюю скорость перемещения и среднюю путевую скорость для промежутка времени 0 ÷ 7 с.
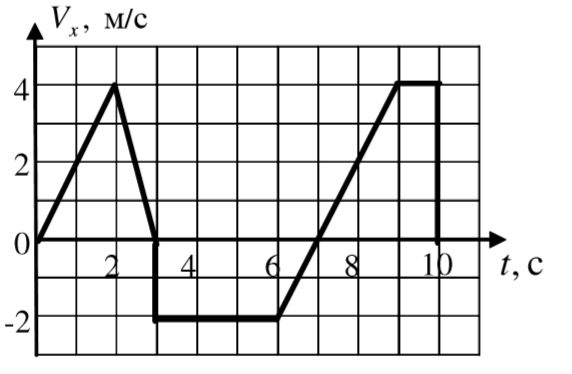
Во-первых, проанализируем, что нам дано. На рисунке представлена зависимость скорости от времени. Вспоминая, что на таком графике функции скорости углом наклона функции к горизонту является ускорение. Замечаем, что здесь присутствуют как равнозамедленные и равноускоренные этапы движения, так и равномерные.
Необходимо определить путь и перемещение. Определения данных величин можете пересмотреть выше.
Мы знаем, что:
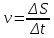
Откуда получим:
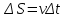
Результат означает, что путь равен площади под кривой (под функцией). В свою очередь, перемещение также равно площади под кривой, но с одним отличием. Путь – сугубо положительная величина, то есть длина траектории. Перемещение – отрезок, соединяющий начальное положение предмета с конечным (проводится из начального в конечное). Напомним о том, что если предмет в процессе движения возвращается в исходную координату, то его перемещение равно нулю.
Таким образом – путь – это величина площади под кривой, вычисленная как сумма площадей различных участков (без учета знака). Перемещение – то же самое, но с учетом знака (перемещение может быть отрицательным, если предмет, например, переместился в направлении отрицательного направления оси).
На рисунке ниже представлен тот же график функции, но уже разбитый на секторы:
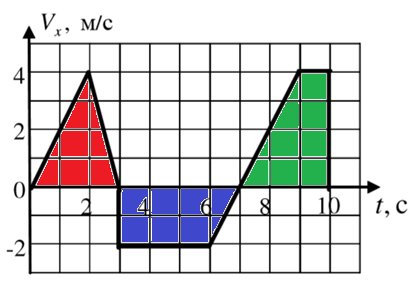
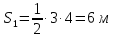
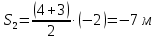
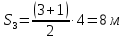
Точка прошла в одном направлении 14 м, и в обратном – 7 м. Таким образом, путь, проходимой точкой за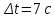
:
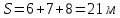
Перемещение точки:
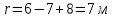
Определим среднюю путевую скорость:
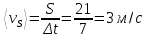
Определим среднюю скорость перемещения:
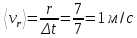
В самом конце повествования было бы справедливым сказать, что везде и всюду в рассказе я использовал понятие «предмет». Такого понятия в физике нет, однако, как показывает практика, оно более привычно, нежели, чем материальная точка или тело. Однако, необходимо дать определения двух последних терминов.
Материальная точка – это некоторый объект, размерами которого в рассматриваемой задаче можно пренебречь. Материальная точка может обладать массой, однако, вся масса сосредоточена в очень малом объеме.
Тело – физический объект, имеющий характеристики длины/площади/объема и массы и размерами которого в рассматриваемой задаче пренебречь нельзя.
Напоследок, приведем важные формулы кинематики, вывод которых и глубокое раскрытие физического смысла в нашем курсе не предусмотрено.
Линейная скорость связана с угловой через радиус траектории:
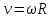
Предположим, что скорость предмета изменяется по величине. Из этого следует, что угловая скорость также будет изменяться по величине. Тогда справедливо записать:
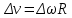
Тангенциальное ускорение есть:
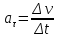
Угловое ускорение есть:
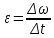
Тогда:
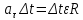
Окончательно получим взаимосвязь тангенциального и углового ускорений:
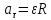
Время, которое требуется предмету для совершения полного оборота по окружности, называется периодом обращения
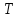.Если предмет совершает полный оборот вдоль окружности, следовательно, он поворачивается на угол, равный
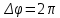. Если предмет движется с постоянной угловой скоростью, то справедливо равенство: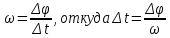 Откуда, получим формулу периода обращения, с учетом, что
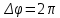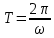
: Угловую скорость часто называют угловой частотой. Однако, на практике оказывается полезным пользоваться и линейной частотой, которую обозначают буквой
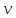. Линейная частота связана с угловой как: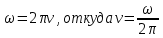 Используя формулу для периода обращения, получим:
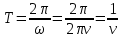
Линейная частота равна числу событий, совершаемых в единицу времени (в секунду). Измеряется она в Герцах [Гц]. Например, лампочка мигает 4 раза в секунду, тогда линейная частота мигания лампочки равна 4 Гц.
Свяжем период обращения с линейной скоростью:
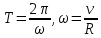
Тогда:
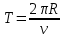
Приведем еще один пример, который было бы неудобно привести в ходе основного повествования. Ранее, по заданному уравнению координаты от времени, мы определяли величину скорости (делали это для линейной функции и искали тангенс угла наклона функции к горизонтальной оси, который численно равен скорости). Однако, существует обратная задача – когда по функции уравнения скорости, зависящей от времени, необходимо определить путь или перемещения, пройденные предметом.
Пример 12.
На графике представлена проекция скорости материальной точки на ось x в зависимости от времени. В начальный момент времени материальная точка находилась в начале координат. Определить ее среднюю скорость перемещения и среднюю путевую скорость для промежутка времени 0 ÷ 7 с.
Во-первых, проанализируем, что нам дано. На рисунке представлена зависимость скорости от времени. Вспоминая, что на таком графике функции скорости углом наклона функции к горизонту является ускорение. Замечаем, что здесь присутствуют как равнозамедленные и равноускоренные этапы движения, так и равномерные.
Необходимо определить путь и перемещение. Определения данных величин можете пересмотреть выше.
Мы знаем, что:
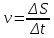
Откуда получим:
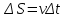
Результат означает, что путь равен площади под кривой (под функцией). В свою очередь, перемещение также равно площади под кривой, но с одним отличием. Путь – сугубо положительная величина, то есть длина траектории. Перемещение – отрезок, соединяющий начальное положение предмета с конечным (проводится из начального в конечное). Напомним о том, что если предмет в процессе движения возвращается в исходную координату, то его перемещение равно нулю.
Таким образом – путь – это величина площади под кривой, вычисленная как сумма площадей различных участков (без учета знака). Перемещение – то же самое, но с учетом знака (перемещение может быть отрицательным, если предмет, например, переместился в направлении отрицательного направления оси).
На рисунке ниже представлен тот же график функции, но уже разбитый на секторы:
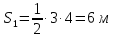
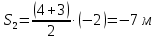
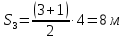
Точка прошла в одном направлении 14 м, и в обратном – 7 м. Таким образом, путь, проходимой точкой за
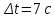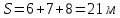
: Перемещение точки:
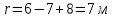
Определим среднюю путевую скорость:
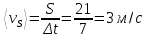
Определим среднюю скорость перемещения:
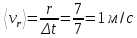
В самом конце повествования было бы справедливым сказать, что везде и всюду в рассказе я использовал понятие «предмет». Такого понятия в физике нет, однако, как показывает практика, оно более привычно, нежели, чем материальная точка или тело. Однако, необходимо дать определения двух последних терминов.
Материальная точка – это некоторый объект, размерами которого в рассматриваемой задаче можно пренебречь. Материальная точка может обладать массой, однако, вся масса сосредоточена в очень малом объеме.
Тело – физический объект, имеющий характеристики длины/площади/объема и массы и размерами которого в рассматриваемой задаче пренебречь нельзя.