ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 02.02.2024
Просмотров: 74
Скачиваний: 0
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Система отсчета перестает быть инерциальной, когда она начинает двигаться с ускорением. И тогда она называется неинерциальной. Однако, как сказано выше, этот вопрос будет поднят подробно в будущем.
Следующим разделом кинематики, который мы рассмотрим, будет вращательное движение – движение, при котором предмет движется вокруг некоторой оси или точки.
Да, выше мы рассматривали линейное, или, как его еще называют – поступательное движение (это движение, при котором предмет движется вдоль прямой). Да, частично мы касались движения по окружности, и ввели понятие нормального ускорения, однако нормальное ускорение – линейная характеристика, поскольку является мерой того, как часто поворачивает вектор линейной скорости
.Теперь пришло ввести понятия угловых величин – величин кинематики, используемых при вращательном движении.
В поступательном движении мы характеризовали положение предмета с помощью координаты. Однако, в ряде задач на вращательное движение оказывается удобным ввести понятие угла поворота
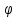.Угол поворота – величина, характеризующая положение предмета, движущегося по окружности (то есть, показатель того, на какой угол повернулся предмет относительно некоторого начального значения). Сделаем рисунок:
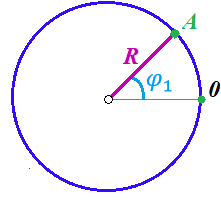
На рисунке представлен предмет А, который может двигаться по окружности радиусом
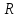. Изначально, предмет расположен в точке, повернутой на угол 
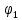относительно горизонтального выбранного нуля. Предположим, что предмет переместился по окружности и стал повернут на угол 
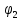. Сделаем рисунок: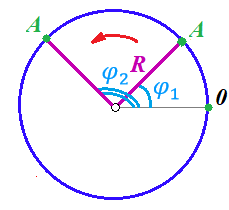
Мы видим, таким образом, что предмет A повернулся на угол:
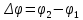
Обратите внимание! Для задания угла поворота не нужен никакой нулевой угол, поскольку он полностью определяется углом между начальным и конечным положениями предмета на окружности:
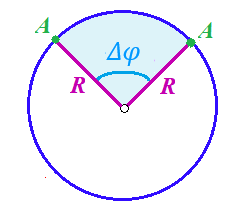
В этом и состоит удобство использования вращательных величин. Система координат, в которой положение предмета относительно центра окружности характеризуется только расстоянием от центра окружности до любой из ее точек (радиусом R) и углом поворота (φ) называется плоской круговой системой координат (на самом деле, пользуются сферической системой координат, в которой присутствует еще один угол пространственного положения, поскольку сфера – объемное тело, но в нашем курсе такое рассматриваться не может).
Сделаем промежуточный вывод: при вращательном движении аналогом координаты предмета (как в поступательном движении) является угол поворота φ.
Угол поворота измеряется либо в градусах (как у гражданских), либо в радианах [рад].
Приведем рисунок:
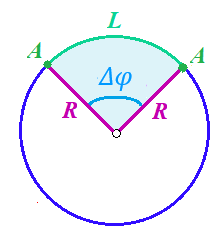
Угол поворота определяется следующим фундаментальным геометрическим равенством:
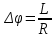
– длина сектора дуги.Вполне естественно, что угол поворота при движении различных предметов может изменяться с разной быстротой.
В поступательном движении характеристикой быстроты изменения координаты предмета с течением времени является скорость
. Во вращательном движении аналогичным параметром является угловая скорость – величина, характеризующая быстроту изменения угла поворота предмета с течением времени.В определении направления угловой скорости есть нечто непохожее на определение направления линейной скорости предмета (в поступательном движении все очевидно – вектор скорости направлен туда, куда движется предмет).
Простота вращательного движения состоит в том, что возможно всего лишь два направления вращения – либо по часовой стрелки, либо против часовой.
Приведем рисунок:
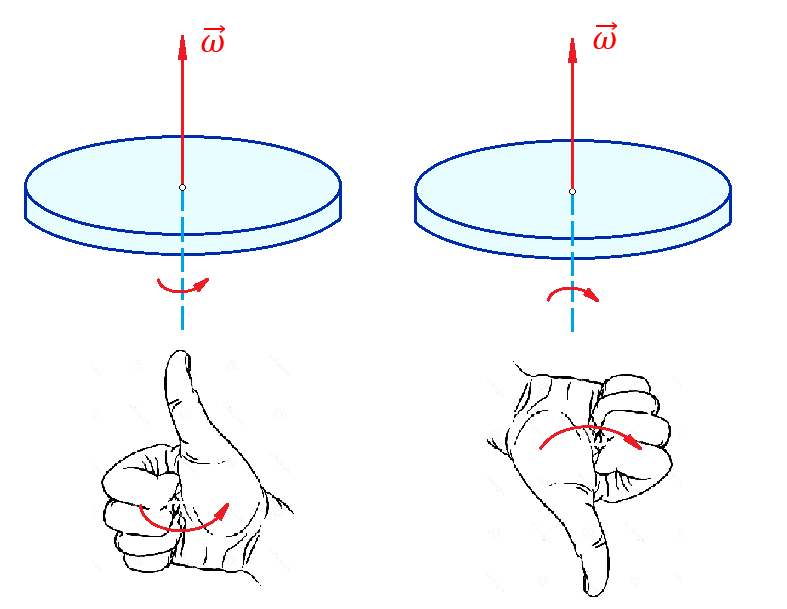
На рисунке выше изображены два вращающихся диска. Левый диск вращается против часовой стрелки, а правый – по часовой.
Направление вращения – это не то же самое, что и направление угловой скорости. Для определения направления угловой скорости используют правило правой руки:
4 пальца правой руки направляем по вращению диска, тогда большой палец покажет направление угловой скорости. Рекомендуется проделать определение направления самостоятельно.
Если бы мы смотрели на вращающийся диск сверху, то картина имела бы следующий вид:
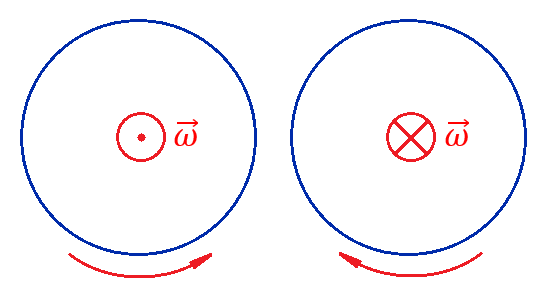
Направление «на нас» отмечается кружком с точкой, направление «от нас» отмечается кружком с крестиком.
Вернемся к раскрытию понятия угловая скорость. Согласно выше сказанному, угловая скорость может быть вычислена следующим образом:
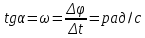
Формула получена аналогично формуле, рассмотренной выше (мы рассматривали линейную зависимость координаты предмета от времени, выбрали два момента времени и соответствующие этим моментам времени координаты, отметили угол α – угол наклон функции к горизонту и затем записали выражение для тангенса этого угла наклона, который и оказался равным скорости).
Из этого следует, что угловая скорость есть тангенс угла наклона функции угла поворота, зависящего от времени.
Как и ранее, если дана линейная зависимость угла поворота от времени, то угловая скорость будет постоянной (так как угол наклона не меняется).
Угловая скорость, как и линейная, является векторной величиной. Однако, мы не будем касаться случаев, когда предмет может менять направление вращения, поскольку это выходит далеко за рамки курса. В кинематике поступательного движения параметром, характеризующем быстроту изменения скорости по величине было тангенциальное ускорение.
В кинематике вращательного движения параметром, характеризующим быстроту изменения величины угловой скорости, является угловое ускорение:
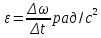
То есть, угловое ускорение есть тангенс угла наклона функции угловой скорости, зависящей от времени. Разумеется, постоянным угловое ускорение будет только тогда, когда зависимость угловой скорости от времени линейная.
Очевидно, что если вектор угловой скорости и углового ускорения имеют одно направление, то движение будет ускоренным
, иначе – замедленным (добавим: если угловое ускорение постоянно по величине и направлению, то движение будет либо равнозамедленным, либо равноускоренным).
Напоследок, запишем уравнения кинематики вращательного движения, подходящие для равномерного или равноускоренное движений:
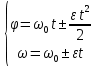
Приведем рисунок, на котором изобразим три различных случая движения предмета по окружности:
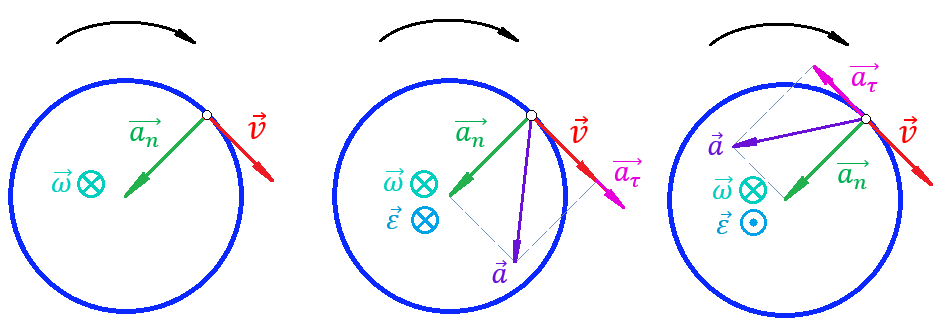
Крайний рисунок слева. Предмет движется по окружности с постоянной по величине линейной скоростью
. Тангенциальное ускорение 
равно нулю, поскольку величина линейной скорости постоянно. Однако, вектор скорости поворачивается, следовательно, предмет обладает нормальным ускорением. Угловая скорость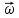 
, согласно правилу правой руки, направлена от нас (черной стрелкой показано направление вращения предмета). Угловое ускорение 
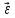равно нулю, поскольку угловая скорость не меняется по величине (по направлению угловая скорость также постоянна, все время направлена от нас).Центральный рисунок. Предмет движется вдоль окружности с изменяющейся по величине линейной скоростью. Следовательно, предмет обладает тангенциальным ускорением. На рисунке тангенциальное ускорение и линейная скорость сонаправлены, это значит, что движение ускоренное. Нормальное ускорение также присутствует, поскольку вектор скорости постоянно поворачивается в процессе движения. Угловая скорость направлена от нас, но уже не постоянная по величине (судя по сказанному выше, она увеличивается, поскольку движение ускоренное). Угловое ускорение направлено от нас, то есть направлено туда же, куда и угловая скорость, поскольку движение – ускоренное.
Крайний рисунок справа. Предмет движется вдоль окружности с изменяющейся по величине линейной скоростью. Следовательно, предмет обладает тангенциальным ускорением. На рисунке тангенциальное ускорение и линейная скорость противоположно направлены, это значит, что движение замедленное. Нормальное ускорение также присутствует, поскольку вектор скорости постоянно поворачивается в процессе движения. Угловая скорость направлена от нас, но уже не постоянная по величине (судя по сказанному выше, она уменьшается, поскольку движение замедленное).