ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 02.02.2024
Просмотров: 70
Скачиваний: 0
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
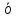льшую величину, чем координата предмета 2. Из этого следует, что скорость предмета 1 больше, чем скорость предмета 2, поскольку: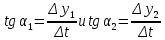
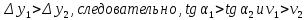
Приведем еще один пример для закрепления изученного материала. На рисунке ниже изображены три функции координат от времени (функции координат трех движущихся предметов в зависимости от времени):
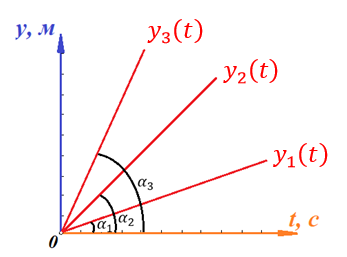
Из сказанного выше сразу становится ясно, что наибольшей скоростью обладает предмет 3 – его функция координаты имеет наибольший угол наклона α. Если это не сразу очевидно, то рекомендуется проделать те же действия, что мы проделали для сравнения скорости двух предметов (за одно и то же время
измерить 
для каждой функции).Выше нами было упомянуто, что скорость предмета не всегда является постоянной (изображение углов наклона функции для примера с параболической зависимостью координаты от времени).
Если мы установили, что скорость – есть характеристика того, как быстро координата предмета изменяется при его движении с течением времени, то наверняка, должна существовать характеристика того, как быстро меняется скорость предмета с течением времени. Да, она существует, и называется она – ускорение.
Мы руководствуемся теми же положениями – для полноты картины нам необходимо знать скорость предмета в каждый момент времени, то есть нам необходимо знать зависимость скорости от времени. Для того, чтобы получить выражение, позволяющее вычислить ускорение, рассмотрим график зависимости скорости некоторого предмета от времени (для простоты – вновь линейный).
Допустим, что скорость предмета зависит от времени следующим образом:
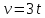
Построим график этой функции:
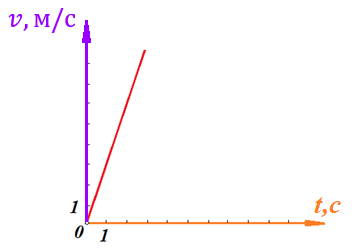
Отметим на графике функции скорости двух точек, в которых побывал предмет в процессе движения:
Из рисунка видно, что нами были выбраны скорост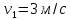и
и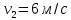 
. Предмет обладал скоростью 
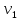в момент времени 
, а скоростью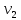 
обладал в момент времени 
.
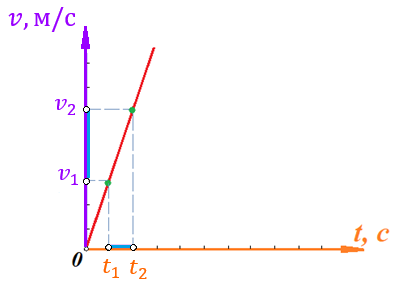
На рисунке выше видно, что мы выделили отрезки, равные разнице между скоростями предмета и разнице между моментами времени, в которых предмет обладал данными скоростями.
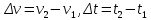
Аналогично рассмотренному выше, мы можем сказать, что за время
скорость предмета изменилась на величину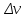 
.Обозначим данные отрезки на рисунке:
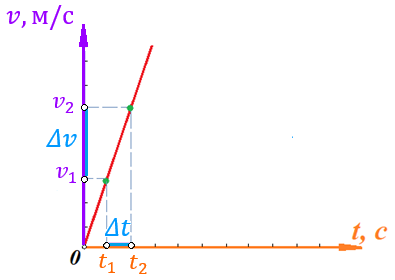
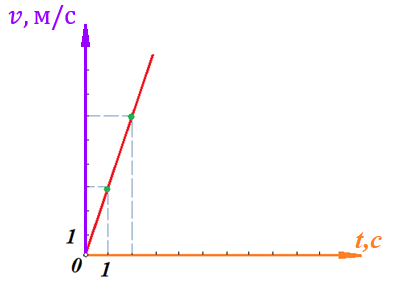
Параллельным переносом перенесем отрезок
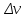вправо, а отрезок вверх: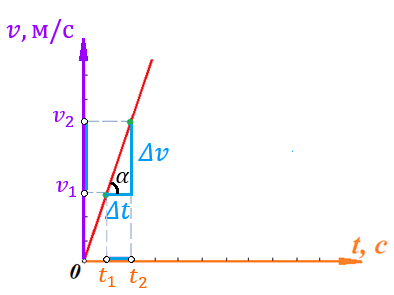
Мы видим, что образуется прямоугольный треугольник. Отметим в этом треугольнике угол α (угол между функцией [прямой красной линией] и горизонталью [осью x]). Как видно из рисунка, данный угол может быть определен, как:
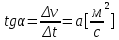
Это есть ни что иное, как ускорение. Таким образом, можем сделать следующий важный вывод: если построить график функции скорости, зависящей от времени, затем выбрать две произвольные скорости и соответствующие им моменты времени, то построив прямоугольный треугольник из отрезков
и , становится возможным определить тангенс угла наклона функции, или же, говоря иначе, определить ускорение.Говоря иначе: ускорение есть характеристика быстроты изменения скорости по величине в течении времени. Однако, необходимо остановиться на этом подробнее.
Скорость – векторная величина, а как известно, люба векторная величина имеет две характеристики – величину и направление. То есть, векторная величина считается полностью заданной, если нам известна ее величина (значение) и направление (куда она направлена).
В процессе движения как величина, так и направление скорости предмета могут меняться. По этой причине в кинематике вводится два ускорения – тангенциальное
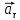и нормальное 
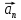.Формула, полученная нами выше для ускорения, определяет тангенциальное ускорение:
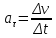
То есть тангенциальное ускорение характеризует быстроту изменения величины скорости с течением времени.
Второе ускорение – нормальное. Нормальное ускорение характеризует быстроту изменения скорости по направлению с течением времени и определяется как:
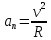
Остановимся подробнее на нормальном ускорении. Нами было сказано, что нормальное ускорение характеризует, как быстро поворачивает скорость предмета в процессе движения с течением времени. Это происходит, например, когда мотоциклист заворачивает на дороге, или, когда человек обходит какое-либо препятствие. Примеров можно привести очень много. Однако в формуле для вычисления нормального ускорения присутствует радиус – почему?
Потому что любой поворот происходит по какой-либо дуге, а каждая дуга характеризуется радиусом, т.е. для каждой дуги можно достроить окружность. На рисунке ниже представлены три случая, когда предмет движется по дуге различного радиуса:
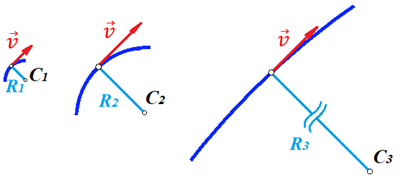
Предполагая, что скорость движения предмета во всех трех изображенных случаях одинакова, мы понимаем, что наибольшее нормальное ускорение будет на крайнем рисунке слева – там наименьший радиус кривизны дуги, по которой движется предмет. То есть, вектор скорости движущегося предмета на крайнем рисунке слева чаще всего поворачивает в этом случае.
Крайний рисунок справа – там предмет движется по дуге с очень большим радиусом, то есть, вектор скорости в этом случае поворачиваться будет медленнее, чем в двух других случаях.
Для лучшего понимания данных рисунков можно привести аналогию. Движение предмета на крайнем рисунке слева можно ассоциировать с движением человека вокруг небольшого магазина, а крайний рисунок справа – движение человека вдоль поверхности Земли. В первом случае человек будет часто заворачивать, то есть обладать большим нормальным ускорением, а во втором – при таком огромном радиусе траектории – мы даже не поймем, что вектор нашей скорости поворачивает, то есть будет обладать очень малым нормальным ускорением.
Внесем дополнительную ясность, рассмотрев следующие возможные случаи движения предмета:
1. Предмет движется строго по прямой с постоянной по величине скоростью. В таком случае предмет не имеет ни тангенциального, ни нормального ускорений, поскольку в процессе движения не изменяется ни величина скорости, не ее направление.
2. Предмет движется строго по прямой с изменяющейся по величине скоростью. В данном случае предмет обладает тангенциальным ускорением, но не обладает нормальным, поскольку в процессе движения меняется величина скорости, но не меняется направление вектора скорости.
3. Предмет движется по дуге с постоянной по величине скоростью. В данном случае предмет не обладает тангенциальным, но обладает нормальным ускорением, поскольку в процессе движения изменяется направление вектора скорости, а величина скорости – постоянна.
4. Предмет движется по дуге с изменяющейся по величине скоростью. В данном случае предмет обладает и тангенциальным, и нормальным ускорениями, поскольку в процессе движения меняется и величина скорости, и ее направление.
Обратите внимание! Речь идет именно о повороте вектора скорости в процессе движения. Если предмет двигался, предположим, слева направо, а затем повернуло и начало движение справа налево, то в данном случае нормального ускорения не будет, поскольку предмет, двигаясь в одном направлении, чтобы начать двигаться в противоположном, должно остановиться, а это считается уже за новый процесс движения. Поэтому, важно понимать, что речь идет именно о повороте вектора скорости в процессе движения, и нормальное ускорение – характеристика, как быстро происходит поворот скорости в процессе движения.
Остановимся на одном важном моменте. Выше мы определили, что если скорость движущегося предмета изменяется по величине, то данный предмет обладает тангенциальным ускорением. Однако, скорость может как увеличиваться, так и уменьшаться по значению. Движение, при котором величина (модуль) скорости движущегося предмета увеличивается – называется ускоренным, а движение, при котором модуль скорости уменьшается – называется замедленным. Если же предмет движется с постоянной по модулю скоростью (модуль скорости постоянен), то такое движение называется равномерным.
Однако, на этом классификация движения не исчерпывается. Тангенциальное ускорение может быть и постоянным, и переменным по величине. Приведем выше рассмотренный пример еще раз:
На данном рисунке нами был построен график функции скорости, зависящей от времени как
, т.е. скорость зависит от времени линейно. Как видно из рисунка, тангенциальное ускорение численно равно тангенсу угла между функцией (красная линия) и горизонталью (ось х). В данном примере угол наклона постоянен, следовательно, и тангенс этого угла постоянен, и окончательно – постоянно тангенциальное ускорение. Такое справедливо только для линейной зависимости скорости от времени. Если тангенциальное ускорение постоянно и не зависит от времени, то такое движение называется либо равноускоренным (модуль скорости увеличивается), либо равнозамедленным (модуль скорости уменьшается).
Если же угол наклона функции скорости постоянно меняется, то такое движение будет просто ускоренным, или замедленным, поскольку ускорение уже не является постоянным (то есть, ускорение является постоянным только тогда, когда скорость зависит от времени линейно, т.к. только в этом случае угол наклона функции остается постоянным).
Перейдем к дальнейшему изучению структуры кинематики. В процессе движения предмет движется согласно различного вида уравнениям координат. Для характеристики расстояния, пройденного предметом в процессе движения, существует несколько важных терминов.
Траектория – это линия (кривая, прямая), которую описывает предмет в процессе своего движения (кривая, вдоль которой движется предмет). Траектории могут иметь бесконечно разнообразный вид, однако в заданиях ЕГЭ это либо прямая, либо парабола.