ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 02.02.2024
Просмотров: 73
Скачиваний: 0
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Обратите внимание, что во втором варианте вывода выражение:
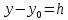
Поскольку начальная координата предмета при таком расположении осей равна нулю, а конечная – высоте
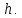
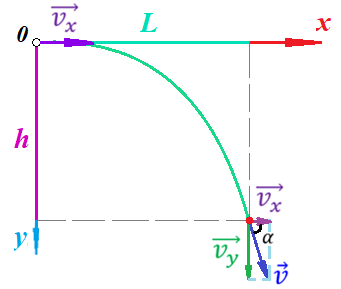
Также заметим, что вертикальная и горизонтальная скорости направлены во взаимно перпендикулярных плоскостях. Из рисунка видно, что их векторная сумма дает некоторую скорость
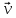. Это скорость и есть та самая скорость, с которой предмет движется по траектории. Полная скорость вычисляется как: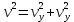
Для горизонтального бросания в качестве итога можно привести следующие формулы:
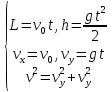
Пример 9. Бросок предмета с поверхности Земли с начальной скоростью
, направленной под углом α к горизонту.
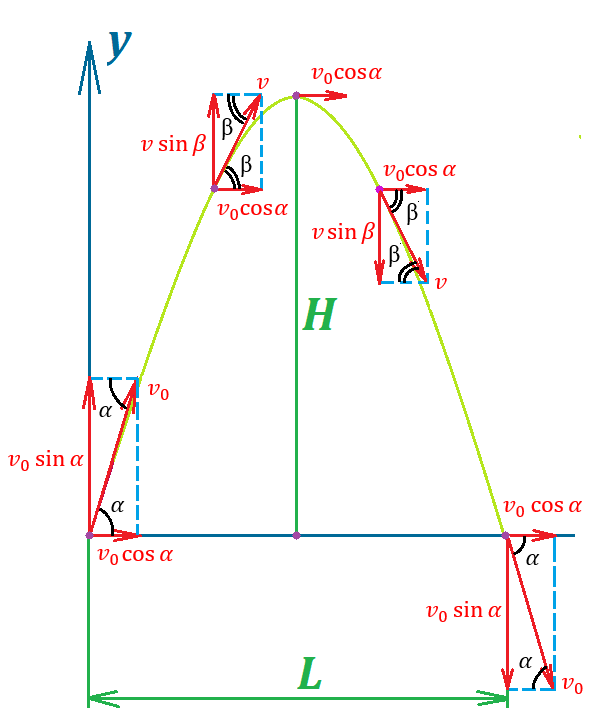
В данной задаче начальная скорость направлена ни вдоль оси х, ни вдоль оси y. Тогда для того, чтобы записать уравнения кинематики по осям координат, необходимо сделать проекции начальной скорости на ось х и ось y.
Из рисунка видно, что:
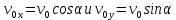
Запишем уравнения кинематики для оси х:
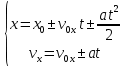
Изначально предмет находится в начале координат, следовательно,
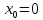.Начальная скорость вдоль оси x имеет величину
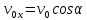.Вдоль горизонтальной оси никакие силы не действуют, следовательно, ускорение равно нулю.
Вектора
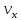и 
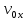направлены вдоль положительного направления оси х, следовательно будут иметь знак «+» в уравнениях.С учетом всего выше сказанного, имеем:
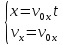
Горизонтальную координату в конце движения, как и в предыдущем примере, назовем дальностью и обозначим как
.Заметим также, что предмет достигает дальности на протяжении всего полета, то есть справедливо дать индекс у времени движения. Окончательно получим:
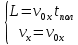
Теперь составим уравнения для оси y:
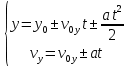
Начальная координата по оси
равна нулю, конечная – равна высоте подъема. Начальная скорость вдоль оси равна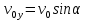 
. Единственное ускорение, существующее в вертикальной плоскости – ускорение свободного падения 
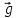. Поскольку ось y направлена вверх, то начальная скорость 
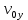, а также скорость 
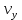будут иметь положительные знаки, а ускорение свободного падения направлено вниз, следовательно, будет записано со знаком минус. Получим предварительно:
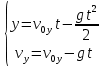
Обратим внимание, что максимальная высота подъема достигается в верхней точке траектории. В этой точке вертикальная скорость обращается в ноль, то есть дальнейший подъем вверх прекращается.
Следовательно,
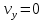.Заметим, что время подъема предмета до максимальной высоты в два раза меньше времени полета (времени, на котором достигается дальность полета). Тогда, с учетом всего вышесказанного, получим:
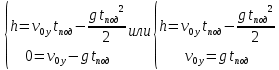
Таким образом, исходная система уравнений кинематики для броска под углом к горизонту имеет следующий вид:
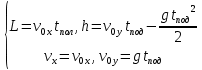
Поставим себе задачу – получить формулы для высоты и дальности, в которых будут присутствовать только начальная скорость и угол, под которым совершен бросок.
Приступим:
Из уравнения скорости для оси y определим время подъема:
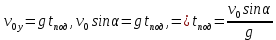
Очевидно, что время полета:
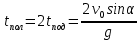
Теперь можем определить дальность полета:
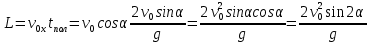
Определим максимальную высоту подъема предмета в процессе движения:
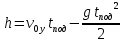
Подставим в это уравнение ранее найденное
:
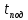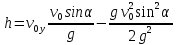
Где
, тогда: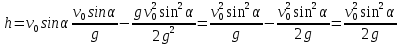
Таким образом, нами были получены важные формулы:
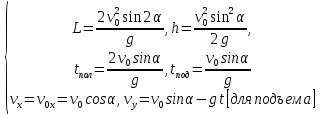
Пример 10. Два предмета, находящиеся на одной вертикали, начинают движение. Один предмет брошен вертикально вверх с начальной скоростью
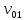, второй начинает вертикальное падение вниз с начальной скоростью 
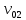. Изначально, расстояние между предметами было равно 
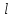. Определить момент времени, когда предметы встретятся.В данной задаче мы уже имеем дело с движением сразу двух предметов одновременно. Причем, эти предметы движутся навстречу друг другу.
Для начала, сделаем рисунок:
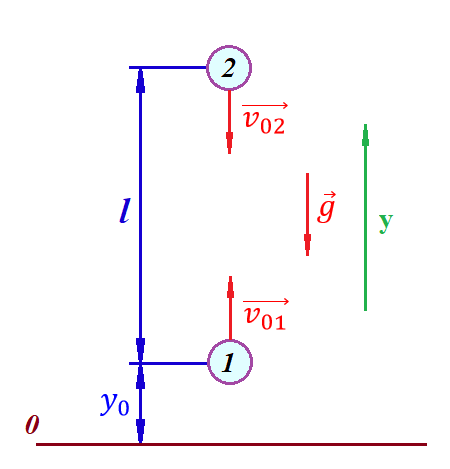
Важный момент! Если мы решаем задачу с двумя предметами, то расстановка знаков у скоростей и ускорений происходит относительно одной и той же оси! Как видно из рисунка, положительное направление оси
направлено вверх.Запишем уравнение координаты для первого предмета:
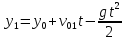
Запишем уравнение координаты для второго предмета:
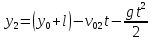
Обратите внимание на знаки у множителей начальных скоростей и ускорений свободны падений у обоих предметов.
Поскольку нас интересует место их встречи, то:
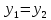
Тогда:
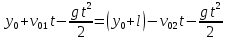
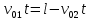
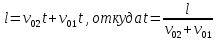
Мы определили время, соответствующее моменту встречи предметов.
Примечание: если бы в задаче был поставлен вопрос об определении координаты, в которой предметы встретятся, то
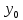можно было бы принять равным нулю, поскольку никакой информации о том, откуда отсчитываются координаты – нет. Именно для этого в решении задачи взята некоторая начальная координата 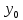(которая, как видно, сокращается и на результат времени встречи не влияет).Приведем альтернативное решение, в котором ось
будет направлена вниз: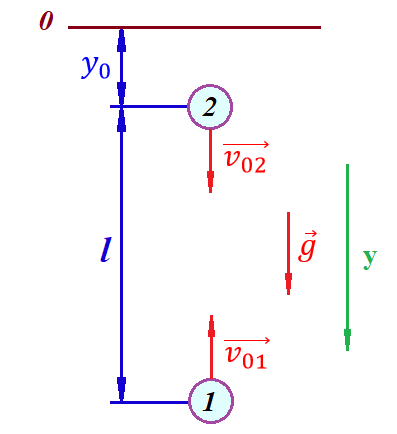
Очевидно, что теперь ноль координат находится сверху. Тогда уравнения координат предметов будут иметь вид:
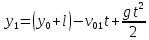
Для второго предмета:
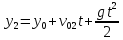
Далее:
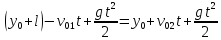
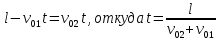
В очередной раз мы показали, что направление оси не влияет на результат, поскольку симметрично «отзеркаливает» направления всех векторов.
Далее, изучим еще один класс задач, предварительно дав несколько определений. В кинематике существуют задачи, в которых ставится целью определить относительную скорость. Относительная скорость – это скорость одного предмета относительно второго, в предположении, что один из этих предметов – покоится.
Поясним на примере. Предположим, что предмет 1 движется направо со скоростью
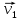, а предмет 2 движется налево со скоростью 
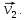Сделаем рисунок: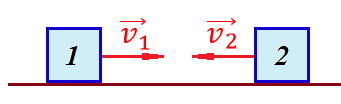
Если поставить задачу вычислить относительную скорость, то необходимо представить, как один из предметов покоится (например, предмет 1). Тогда предмет 2 движется со скоростью:
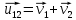
Относительно покоящегося предмета 1. Изобразим это:
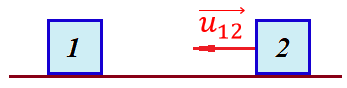
Рассмотренный пример можно привести в ином виде – представить себе два автомобиля, движущихся навстречу друг другу с некоторыми скоростями, тогда скорость их относительного сближения равна сумме скоростей автомобилей.
Если бы предметы 1 и 2 двигались бы в одном направлении (друг за другом), то относительная скорость вычислялась бы как:
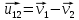
Если бы оба предмета двигались в противоположенные стороны, то их скорость «разбегания» вычислялась бы как:
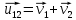
Пример 11. Человек идет с собственной скоростью 5 м/с по вагону. С какой скоростью движется человек относительно вагона, если скорость последнего 40 м/с? С какой скоростью человек движется относительно Земли?
Поскольку вагон покоится относительно человека, то его скорость относительно вагона равна 5 м/с.
Относительно Земли скорость человека будет равна 45 м/с.
Рассмотрение относительной скорости было неслучайным. Пришло время определить рассматриваемые нами системы отсчета (системы координат, в которых помимо местоположений предметов нам известно течение времени, то есть мы обладаем измерителем времени). В нашем курсе мы будем работать только в инерциальных системах отсчета.
Инерциальные системы отсчета – это такие системы отсчета, которые покоятся, или же движутся с постоянной скоростью.
Более подробно этот вопрос будет раскрыт в разделе динамика. Однако, рассмотренный выше пример с вагоном, демонстративен. Система отсчет вагона, движущегося с постоянной скоростью, для предмета является инерциальной. Система отсчета Земли, покоящейся относительно человека, также является инерциальной.