ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 02.02.2024
Просмотров: 64
Скачиваний: 0
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
| Среднедушевые денежные доходы, тыс. руб. в месяц | Доля населения, % |
| До 11 | 10+13+ 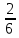 *3 *3 |
| 11-22 | 2+4+6 |
| 22-33 | 14+10+4 |
| 33-44 | 6+15+3 |
| 44-55 | 1+5+6 |
| Итого | 100 |
Вопрос 13 (20 баллов) С целью изучения среднедушевого денежного дохода пенсионеров города проведено 10%-ное выборочное наблюдение методом бесповторного случайного отбора. Численность пенсионеров города составляет 90 человек. По результатам обследования их среднедушевой доход составляет 5000 руб., среднее квадратическое отклонение 3,05 руб. Определите пределы среднедушевого дохода пенсионеров города при значении доверительной вероятности …. Например, 0,954.
1) Найдем генеральную совокупность N
10% - 90
100% - 900
2) Средняя ошибка выборки:
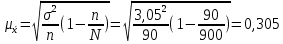 руб.
руб.3) Пределы. Наша вероятность 0,954
| Значение доверительной вероятности P(t) | 0,683 | 0,954 | 0,997 |
| Значение коэффициента доверия t | 1,0 | 2,0 | 3,0 |
Определим предельную ошибку выборки при вероятности 0,954:
 = t *
= t *  = 2*0,305 = 0,61 руб.
= 2*0,305 = 0,61 руб.Доверительный интервал для генеральной средней определяется неравенством:
????̃ − ????????̃ ≤ ????̅ ≤ ????̃ + ????????̃
Определим доверительный интервал для генеральной средней:
5000-0,61≤ x≤ 5000+0,61
4999,39≤ x≤ 5000,61
Вопрос 14 (20 баллов) Имеются данные о распределении населения Российской Федерации по величине среднедушевых денежных доходов в 2017 г.:
| Среднедушевые денежные доходы, тыс. руб. в месяц | Доля населения, % | Накопленная частота |
| 30-40 | 7 | 7 |
| 40-50 | 10 | 17 |
| 50-60 | 17 | 34 |
| 60-70 | 19 | 53 |
| 70-80 | 18 | 71 |
| 80-90 | 10 | 81 |
| 90-100 | 9 | 90 |
| 100-110 | 6 | 96 |
| 110-120 | 4 | 100 |
Определите: средний денежный доход, модальный денежный доход, медианный денежный доход, третий квартиль, децильный коэффициент дифференциации доходов населения, коэффициент фондов.
Средний денежный доход:
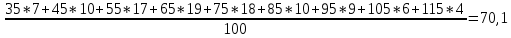
Модальный денежный доход:
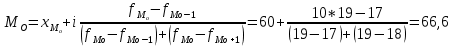
Медианный денежный доход:
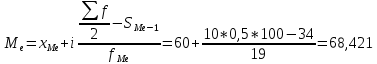
Третий квартиль:
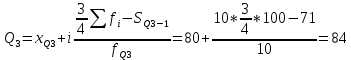
Децильный коэффициент дифференциации доходов населения:
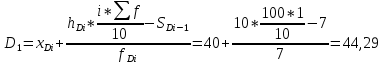
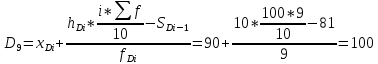
Коэффициент:
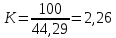
Коэффициент фондов:
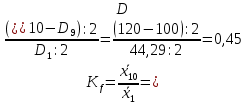
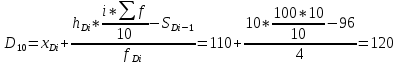
Вопрос 15 (20 баллов) По ряду предприятий получены данные, представленные в таблице. Методом аналитической группировки установите наличие и направление корреляционной связи между факторным признаком «Стоимость основных средств» (X) и результативным признаком «Выручка» (Y). Постройте линейную однофакторную регрессионную модель зависимости Y от X.
| № п/п | Числен-ность работ-ников, чел. | Основные средства, тыс. руб. | Выручка, млн руб. | № п/п | Числен-ность работ-ников, чел. | Основные средства, тыс. руб. | Выручка, млн руб. |
| 1 | 20 | 98 | 11 | 6 | 18 | 88 | 10 |
| 2 | 13 | 76 | 6 | 7 | 11 | 73 | 4 |
| 3 | 15 | 82 | 8 | 8 | 16 | 84 | 5 |
| 4 | 14 | 79 | 7 | 9 | 12 | 74 | 7 |
| 5 | 17 | 87 | 9 | 10 | 12 | 73 | 6 |
Аналитическая таблица для анализа корреляционной связи между изучаемыми признаками имеет следующий вид:
По формуле Стерджесса определим необходимое количество используемых групп:
k = 1+3,322*lg10 = 4
i =
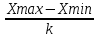 =
= 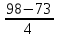 = 6,25
= 6,25| Зависимость выручки от стоимости основных средств | |||
| Группы предприятий по стоимости основных средств, тыс.руб. | Число предприятий, f | Выручка, млн руб. | |
| суммарное значение по группе | в среднем на одно предприятие | ||
| 73-79,25 | 5 | 30 (6+7+4+7+6) | 6 |
| 79,25-85,5 | 2 | 13 | 6,5 |
| 85,5-91,75 | 2 | 19 | 9,5 |
| 91,75-98 | 1 | 11 | 11 |
| Итого | 10 | 73 | 7,3 |
Линейная однофакторная модель
Линейное однофакторное уравнение регрессии имеет вид:
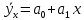
Коэффициенты уравнения регрессии определим по формулам:
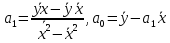
-
X Сумма = 814 -
X Средняя = 81,4 -
X2 Сумма = 66848 -
X2 Средняя = 6684,8 -
Y Сумма = 73 -
Y Средняя = 7,3 -
YX Сумма = 6074 -
YX Средняя = 607,4
a1 =
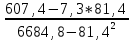 = 0,22
= 0,22a0 = 7,3 – 0,22*81,4 = -10,61
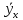 = -10,61+0,22*x – линейная однофакторная модель
= -10,61+0,22*x – линейная однофакторная модельЧем выше стоимость основных средств, тем выше выручка
Вопрос 16 (10 баллов) По приведенным данным рассчитайте по годам размер фонда оплаты труда работников. Определите среднегодовой абсолютный прирост фонда оплаты труда и среднегодовой темп прироста.
| Год | Среднесписочная численность работников, тыс. чел. | Среднемесячная заработная плата, руб./чел. | Темп прироста |
| 2010 | 50 | 35000 | 100 |
| 2012 | 70 | 60000 | 171,43 |
| 2014 | 100 | 75000 | 125 |
Среднегодовой абсолютный прирост:
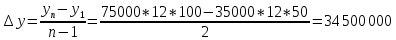
Среднегодовой темп прироста:
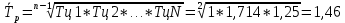
Вопрос 17 (20 баллов) В таблице представлены данные о численности рабочей силы, занятых и безработных.
| Показатель | 2000 г. | 2010 г. | 2020 г. |
| Численность рабочей силы, тыс. чел. – всего | 5200 | 6000 | 6500 |
| Мужчины | 3200 | 3500 | 3300 |
| Женщины | 2000 | 2500 | 3200 |
| в том числе: | | | |
| занятые – всего | 4000 | 4500 | 5200 |
| Мужчины | 2100 | 2500 | 2900 |
| Женщины | 1900 | 2000 | 2300 |
| безработные – всего | 1200 | 1500 | 1300 |
| Мужчины | 1100 | 1000 | 400 |
| Женщины | 100 | 500 | 900 |
Определите за каждый год: структуру рабочей силы по полу, структуру занятых и безработных по полу. Сформулируйте выводы о структурных изменениях в составе рабочей силы, занятых и безработных.
-
Структура рабочей силы по полу
А) 2000 год:
-
Доля мужчин: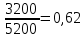
-
Доля женщин: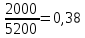
Б) 2010 год:
-
Доля мужчин: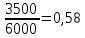
-
Доля женщин: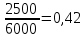
В) 2020 год:
-
Доля мужчин: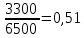
-
Доля женщин: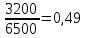
-
Структура занятых по полу
А) 2000 год:
-
Доля мужчин: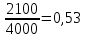
-
Доля женщин: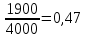
Б) 2010 год:
-
Доля мужчин: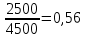
-
Доля женщин: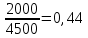
В) 2020 год:
-
Доля мужчин: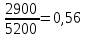
-
Доля женщин: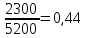
-
Структура безработных:
А) 2000 год:
-
Доля мужчин: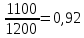
-
Доля женщин: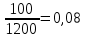
Б) 2010 год:
-
Доля мужчин: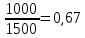
-
Доля женщин: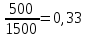
В) 2020 год:
-
Доля мужчин: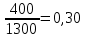
-
Доля женщин: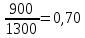
Выводы:
-
В структуре рабочей силы по полу можно увидеть увеличение доли женского пола с течением времени и колебание количества мужчин рабочих в районе 3330 человек. -
В структуре занятых по полу с течением времени количество и мужчин, и женщин возрастает, но количество мужчин остается на порядок выше относительно количества женщин -
В структуре безработных по полу мы наблюдаем понижение числа безработных мужчин и увеличение числа безработных женщин.

