Математическая статистика»

Методические указания для студентов

По выполнению Лабораторной работы

2.1 Лабораторная работа № 1

«Первичная обработка статистических данных»
Из данных, входящих в выборку (табл.1.1) находим и , соответственно наименьшее и наибольшее значения выборки, и вычисляем число , называемое размахом выборки. Размах выборки – это длина основного интервала, в который попадают все значения выборки. Далее значения , называемые вариантами можно упорядочить, то есть расположить в порядке возрастания. Тогда выборка , записанная по возрастанию, называется вариационным рядом. По формуле

,

(2.1)

где целая часть числа , определим число . Данное число задает количество подынтервалов, на которые разбиваем основной интервал . Вычисляем длину подынтервалов по формуле

(2.2)

и затем – границы подынтервалов:

---

.

(2.3)

Находим частоты относительные частоты попадания значений выборки в й подынтервал. Причем должно быть

.

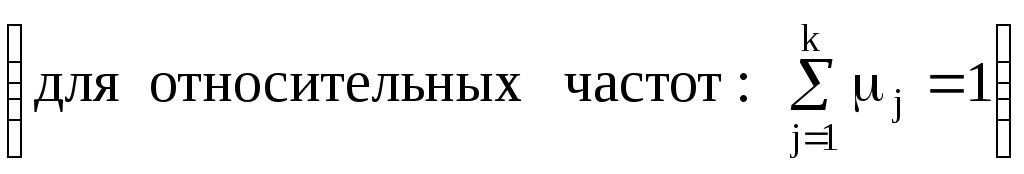В результате проведенных расчетов, получаем две таблицы:
Таблица 2.1

			…
			…

Таблица 2.2

			…
			…

---

Далее, если найти середины подынтервалов:

, то получим еще одну таблицу. ω

Таблица 2.3

			…
			…

В целях наглядности полученных в табл. 2.1, 2.2, 2.3 данных пользуются различными способами их графического изображения. К ним относятся гистограмма и полигон.

Для построения гистограммы относительных частот используем данные табл.2.2. В декартовой системе координат на оси находим значения и и тем самым находим границы основного интервала, в который попадают все значения выборки. Затем на этом интервале откладываем границы подынтервалов. По оси откладываем величины (плотности вероятностей) . Тогда гистограммой относительных частот назовем ступенчатую фигуру, состоящую из прямоугольников, основаниями которых служат частичные подынтервалы длины , а высоты равны числам

---

(плотности вероятностей) . Аналогично, по данным табл. 2.1, строится гистограмма частот.

Для построения полигона относительных частот используем данные табл. 2.3. В декартовой системе координат на оси находим и , то есть изображаем границы основного интервала. Затем наносим значения середин подынтервалов . По оси откладываем значения, соответствующие относительным частотам .

Полигоном относительных частот называют ломаную, отрезки которой соединяют точки .

Данные табл. 2.3 представляют эмпирический закон распределения выборки, а полигон относительных частот есть его визуальное представление.

Эмпирической функцией распределения (функцией распределения выборки) называют функцию , определяющую для каждого значения относительную частоту события .

Таким образом, , где число вариант, меньших , объем выборки.

Для каждой реализации выборки эмпирическая функция распределения однозначно определена и обладает всеми свойствами теоретической функции распределения:

1) значения эмпирической функции принадлежат отрезку

---

;

2) не убывающая функция;

3) если наименьшая варианта, то при ; если наибольшая варианта, то при .

Эмпирическая функция распределения выборки является оценкой теоретической функции распределения генеральной совокупности.

ПРИМЕР 2.1.

Дана выборка из генеральной совокупности объема n=100.

Таблица 2.4

254	1158	522	524	972	736	401	347	208	368
1485	812	1032	226	428	368	676	671	587	701
701	1171	443	683	786	895	267	597	51	941
659	400	484	876	570	241	678	127	728	903
424	245	531	986	1017	429	732	1021	430	153
513	520	221	1074	826	65	389	1180	504	325
294	447	1459	589	307	461	1434	559	837	743
382	387	967	446	763	767	349	853	578	652
285	628	688	517	380	375	878	409	109	621
712	476	432	721	1300	577	580	909	690	757

---

Смотрите также файлы

• Координационными органами рсчс являются.docx

• Отчет. Это отчет. Это отчет. Это отчет. Это отчет. Это отчет. Это отчет. Это отчет. Это отчет. Это отчет. Это отчет. Это отчет. Это отчет. Это отчет. Это отчет.docx

• В географической структуре внешней торговли России основными партнерами торговыми контрагентами остаются промышленно развитые страны. Их доля в российском товарообороте составляет более 60%.docx

• Махачкалу 14. 20, заселение, обед, поиск авто и прогулка по городу. 24. 04. 2022 ранний подъем, ориентировочно в 7 00, тренировка в Тарках.docx

• Реферат по магистерской программе Современные проблемы развития науки, техники и технологии нефтегазовая технике и технологии.docx