1) Находим из выборки и , рассчитываем размах выборки :

; ; .

2) Составим вариационный ряд, для чего всю последовательность выборки расположим в порядке возрастания

51	65	109	127	153	208	221	226	241	245
254	267	285	294	307	325	347	349	368	368
375	380	382	387	389	400	401	409	424	428
429	430	432	443	446	447	461	476	484	504
513	517	520	522	524	531	559	570	577	578
580	587	589	597	621	628	652	659	671	676
678	683	688	690	701	701	712	721	728	732
736	743	757	763	767	786	812	826	837	853
876	878	895	903	909	941	967	972	986	1017
1021	1032	1074	1158	1171	1180	1300	1434	1459	1485

---

3) Задаем число количество частичных подынтервалов, на которое разбиваем нашу выборку : . Исходя из этого вычисляем длину подынтервалов и границы подынтервалов ,

;

;

;

;

;

;

;

;

.

4) Рассчитываем частоты – число попаданий в подынтервалы значений из выборки, то есть .

















.

Контроль:

---

.

На основе полученных данных, заполняем таблицу

	[51; 210,333)	[210,333; 369,666)	[369,666; 528,999)	[528,999; 688,332)	[688,332; 847,665)
	6	14	25	18	16

	[847,665; 1006,998)	[1006,998; 1166,331)	[1166,331; 1325,664)	[1325,664; 1485]
	10	5	3	3

5) Считаем середины подынтервалов и относительные

частоты .

; ;

















.

---

Относительные частоты:

Контроль:

.
В результате имеем таблицу:

Таблица 2.5

	130,6	290	449,3	608,6	768	927,3	1086,6	1246	1405
	0,06	0,14	0,25	0,18	0,16	0,1	0,05	0,03	0,03

6) Из данных табл. 2.5, получим эмпирический закон распределения относительных частот и визуальное его представление, то есть строим гистограмму (рис. 2.1) и полигон распределения относительных частот (рис. 2.2).

---

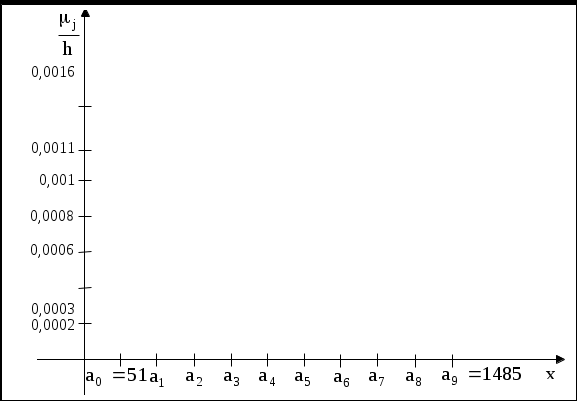
Рис. 2.1

7

Рис. 2.2
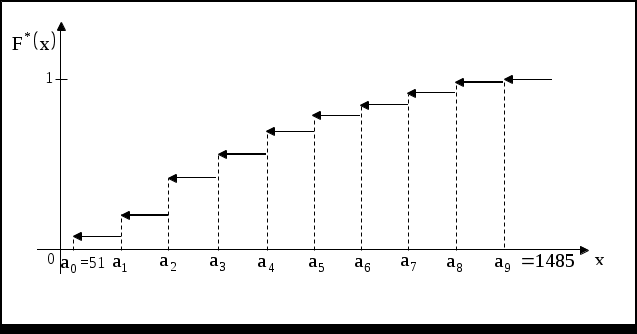
) Составим эмпирическую функцию распределения. По определению, для группированного статистического ряда , имеет вид


Построим график .

2.2 ЛАБОРАТОРНАЯ РАБОТА № 2

Расчет точечных и интервальных оценок генерального математического ожидания и дисперсии
Пусть некоторый параметр генеральной совокупности, который невозможно вычислить. Но знать его значение (хотя бы приближенное, оценочное) надо! Поэтому по выборочным данным производят расчет статистических оценок данного генерального параметра.

Точечной называют статистическую оценку генерального параметра , которая определяется одним числом . Точечная оценка может быть несмещенной и смещенной.

Несмещенной называют такую точечную оценку , математическое ожидание которой равно оцениваемому генеральному параметру при любом объеме выборки, то есть

.

(2.4)

Если равенство (2.4) нарушается, то в этом случае точечная оценка называется смещенной.

Несмещенной оценкой генеральной средней (математического ожидания генеральной совокупности) служит выборочная средняя:

,

(2.5)

---

Смотрите также файлы

• Координационными органами рсчс являются.docx

• Отчет. Это отчет. Это отчет. Это отчет. Это отчет. Это отчет. Это отчет. Это отчет. Это отчет. Это отчет. Это отчет. Это отчет. Это отчет. Это отчет. Это отчет.docx

• В географической структуре внешней торговли России основными партнерами торговыми контрагентами остаются промышленно развитые страны. Их доля в российском товарообороте составляет более 60%.docx

• Махачкалу 14. 20, заселение, обед, поиск авто и прогулка по городу. 24. 04. 2022 ранний подъем, ориентировочно в 7 00, тренировка в Тарках.docx

• Реферат по магистерской программе Современные проблемы развития науки, техники и технологии нефтегазовая технике и технологии.docx