Файл: Лабораторная работа 1 Первичная обработка статистических данных.doc
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 03.02.2024
Просмотров: 25
Скачиваний: 0
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
. Поскольку плотность распределения для нормального закона есть
Тогда
где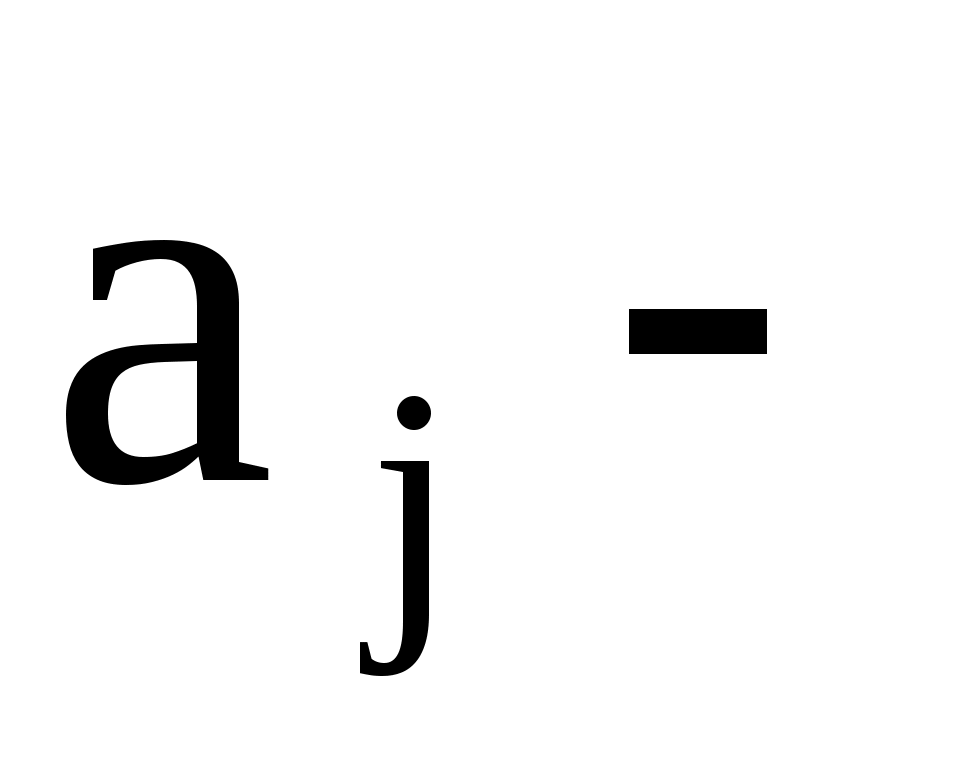 границы частичных интервалов;
границы частичных интервалов;
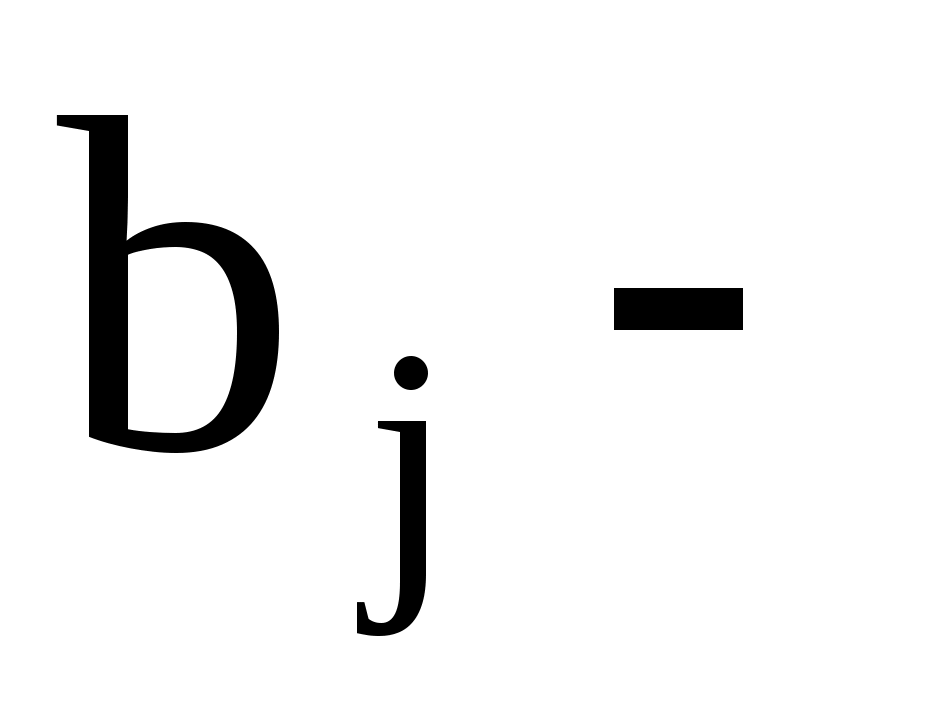 середина
середина  го частичного интервала;
го частичного интервала;
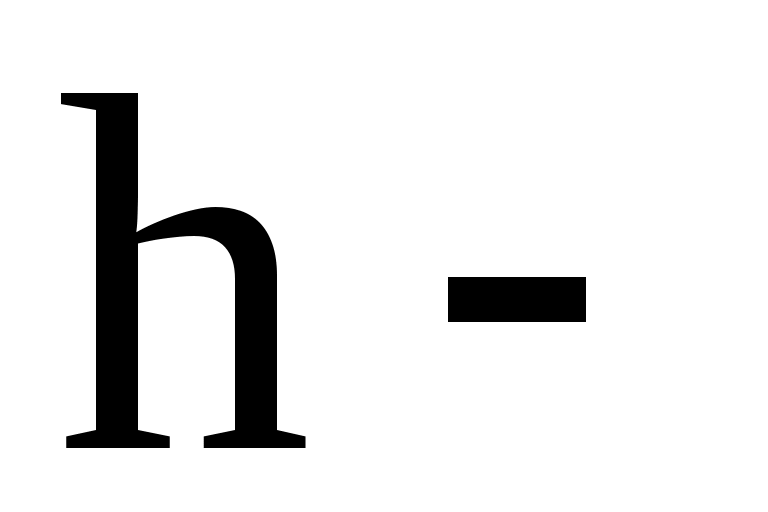 длина частичного интервала (см. формулу (2.2)).
длина частичного интервала (см. формулу (2.2)).
3. Составить сводную таблицу на основе данных табл. 2.3 и рассчитанных теоретических вероятностей:
Таблица 2.6
4. Оценку отклонения эмпирических вероятностей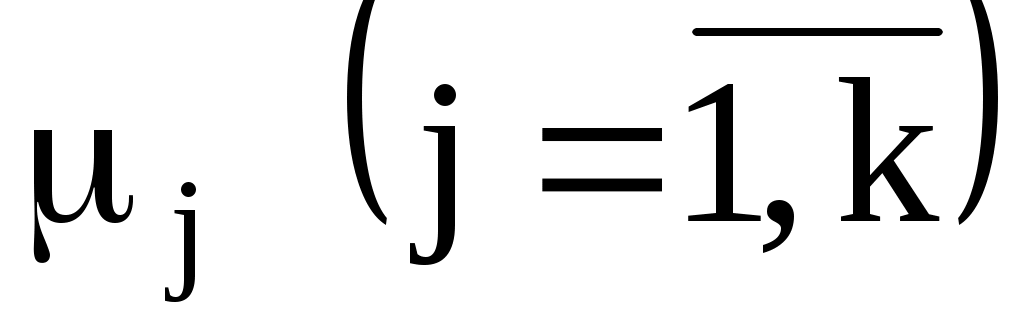 от теоретических вероятностей
от теоретических вероятностей 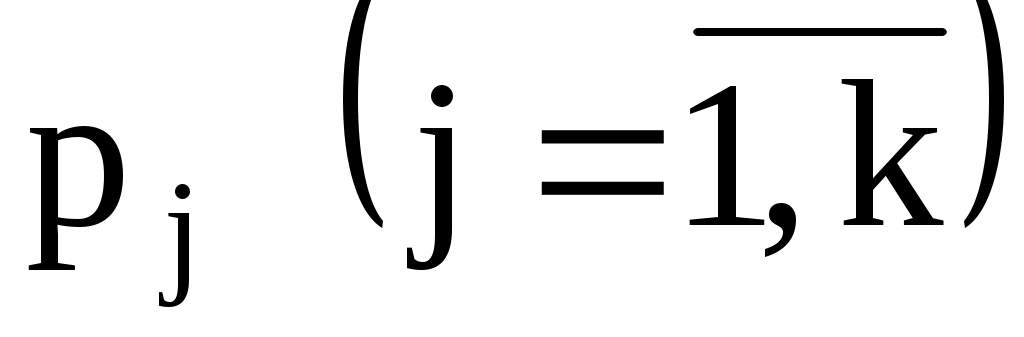 произвести с помощью критерия Пирсона
произвести с помощью критерия Пирсона 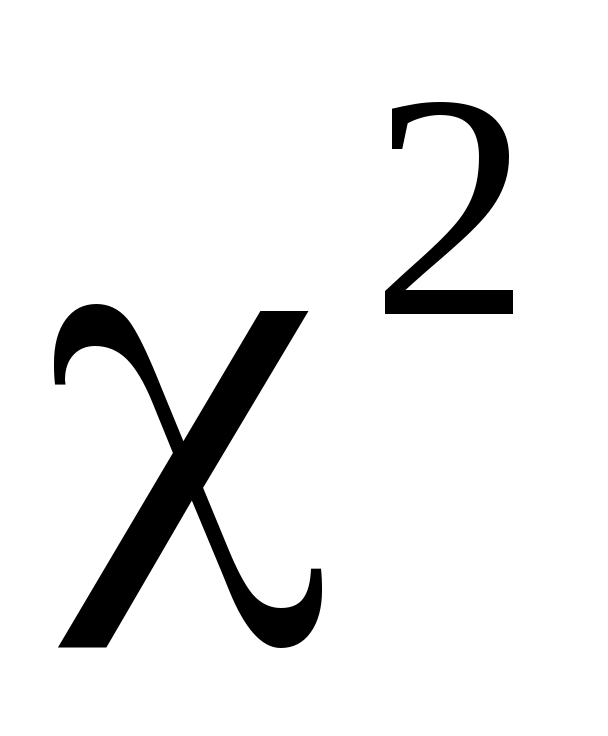 :
:
5. По таблице критических точек распределения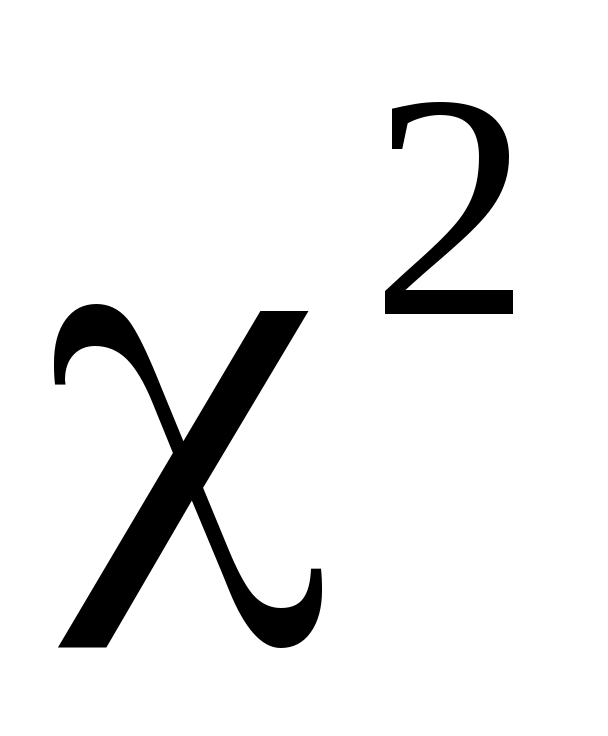 (приложение 4) по заданному уровню значимости
(приложение 4) по заданному уровню значимости  и числу степеней свободы
и числу степеней свободы 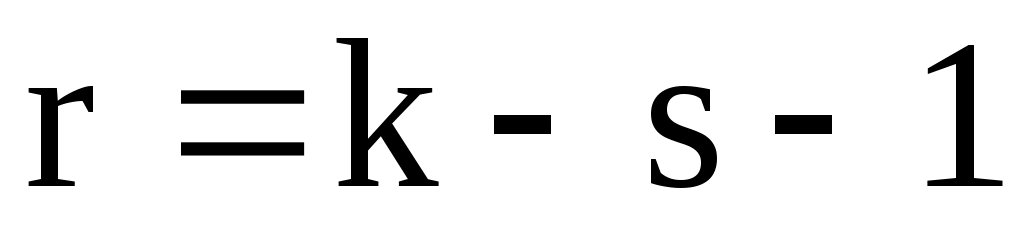 (
( количество подынтервалов,
количество подынтервалов,  - число параметров распределения,
- число параметров распределения, 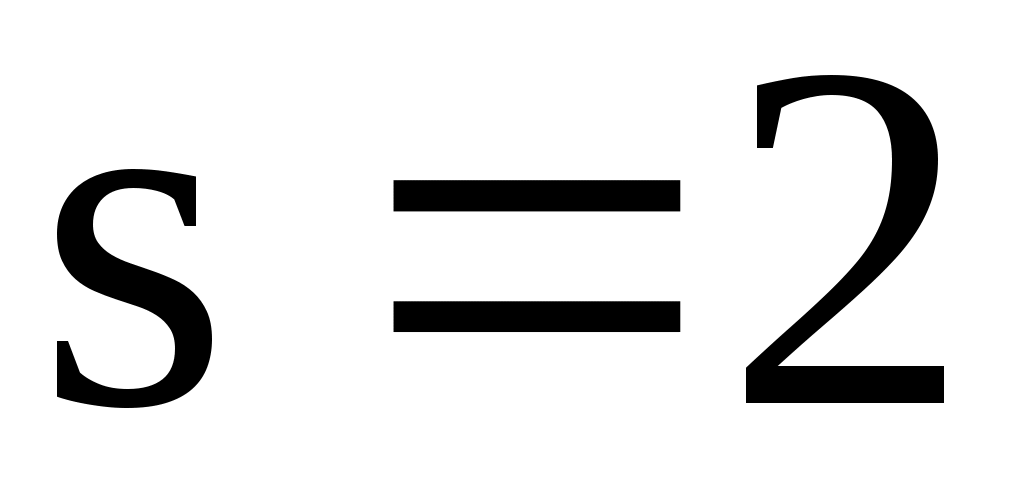 ) найти критическое значение
) найти критическое значение 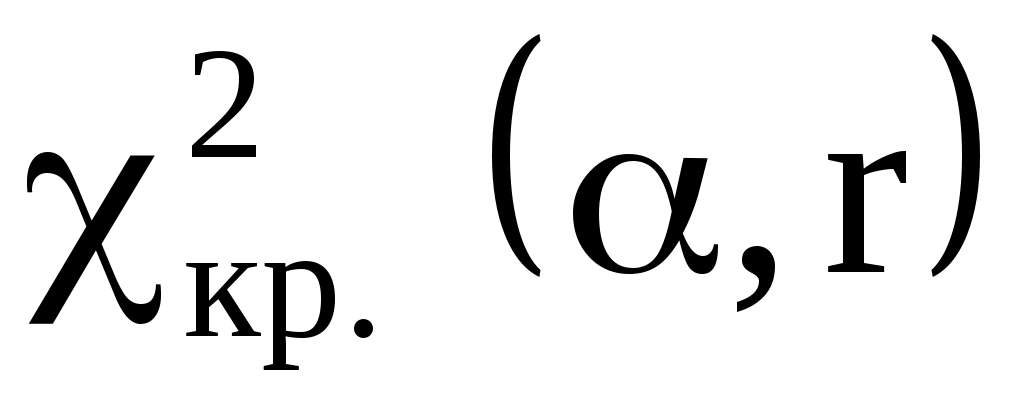 правосторонней критической области.
правосторонней критической области.
Правило 2.1. Если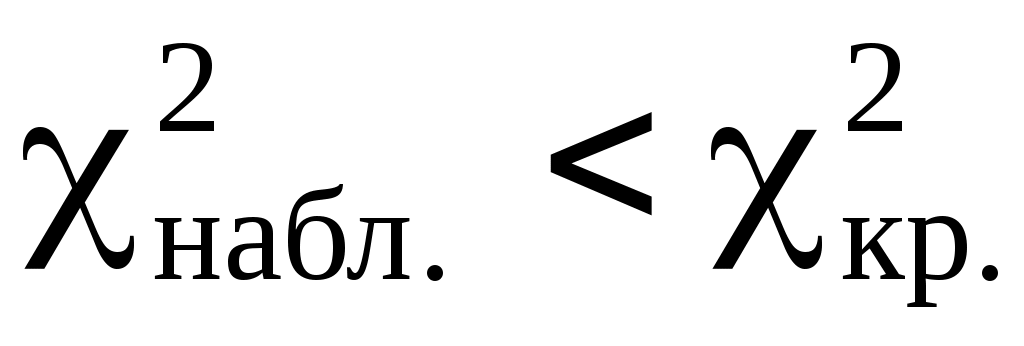 , тогда нет оснований отвергать гипотезу
, тогда нет оснований отвергать гипотезу 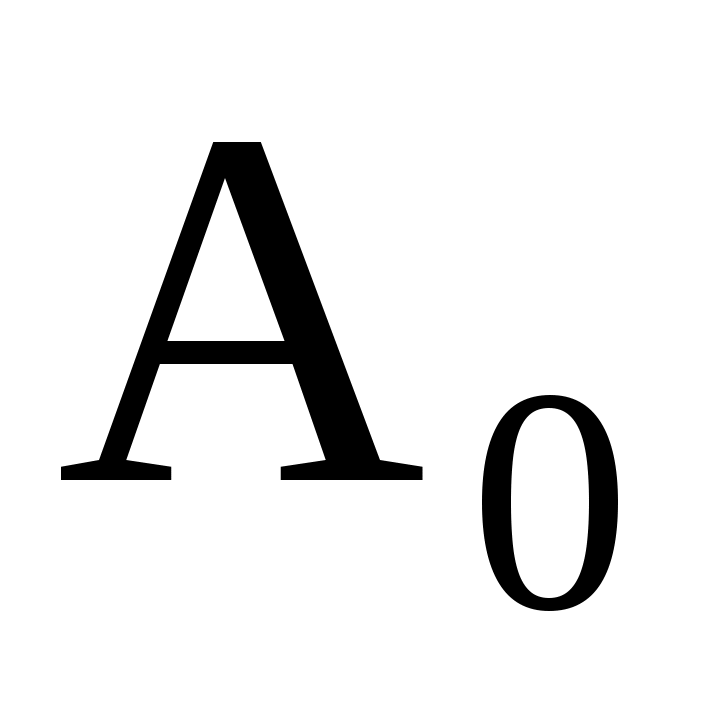 о нормальном распределении генеральной совокупности (то есть эмпирические и теоретические частоты различаются незначимо (случайно).
о нормальном распределении генеральной совокупности (то есть эмпирические и теоретические частоты различаются незначимо (случайно).
Правило 2.2. Если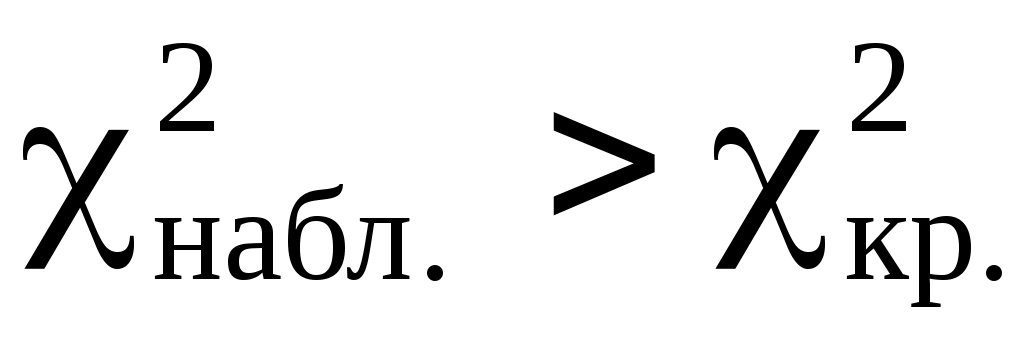 , тогда гипотезу
, тогда гипотезу 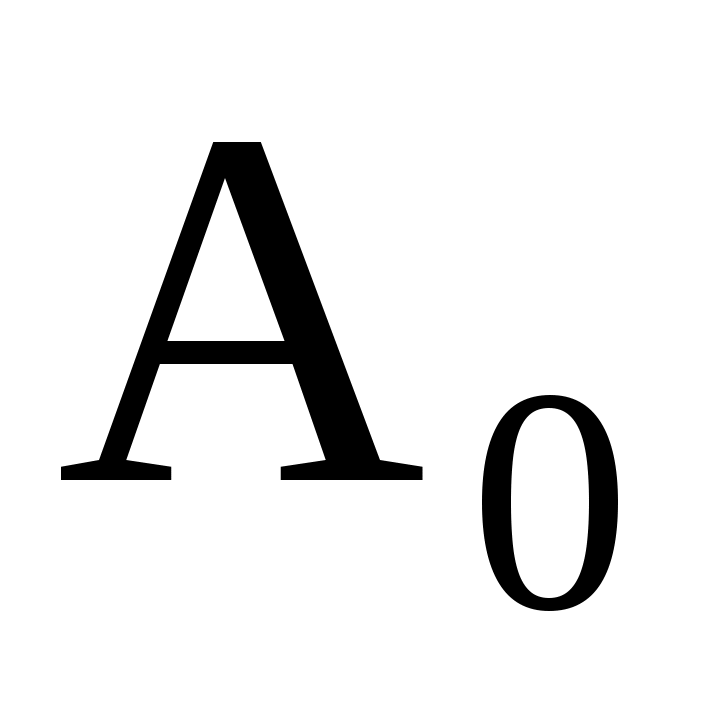 отвергаем.
отвергаем.
Гипотеза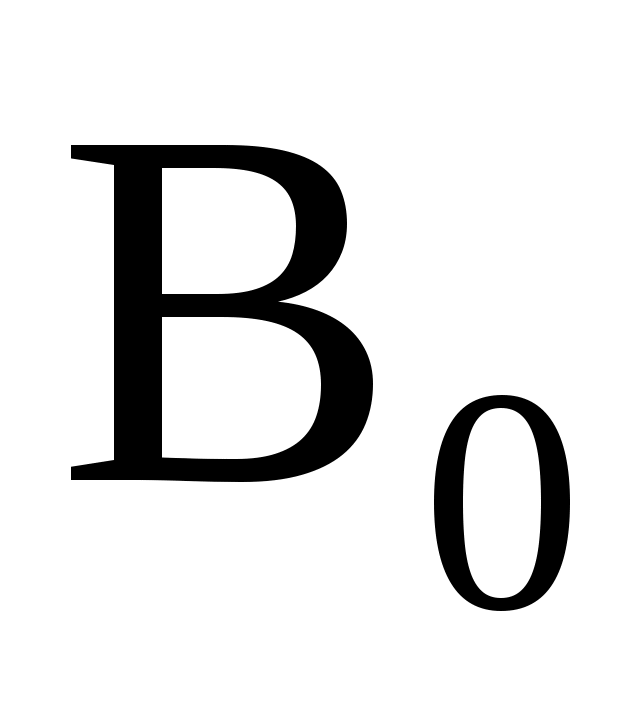 .
.
Для того, чтобы при заданном уровне значимости , проверить гипотезу о показательном распределении генеральной совокупности надо:
, проверить гипотезу о показательном распределении генеральной совокупности надо:
1. Вычислить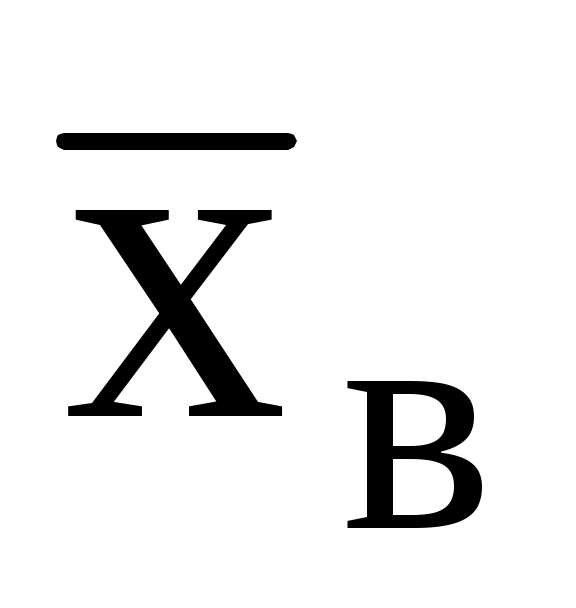 (лабораторная работа № 1). Принять в качестве оценки параметра
(лабораторная работа № 1). Принять в качестве оценки параметра
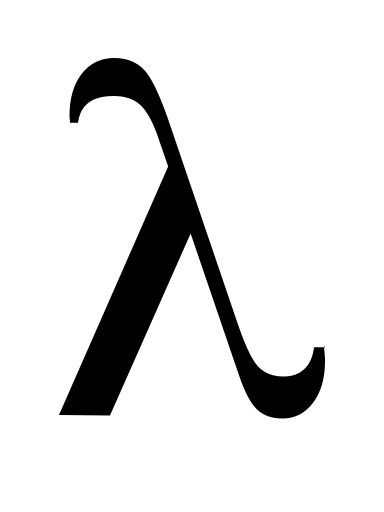 показательного распределения величину, обратную выборочной средней:
показательного распределения величину, обратную выборочной средней:
2. Вычислить теоретические вероятности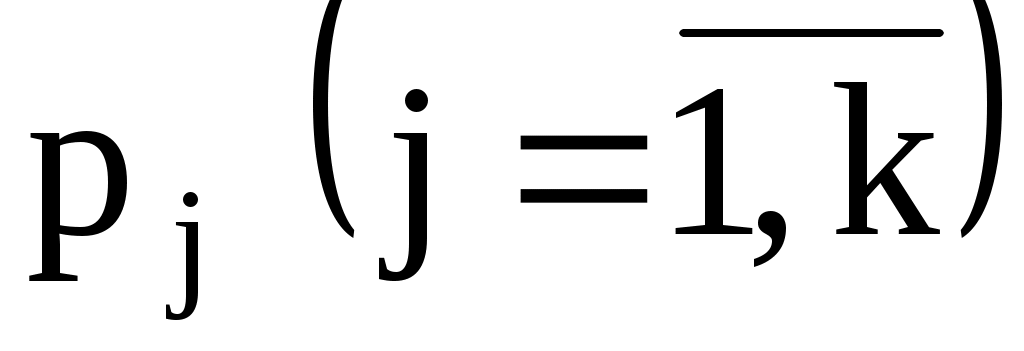 . Поскольку плотность распределения для показательного (экспоненциального) закона есть
. Поскольку плотность распределения для показательного (экспоненциального) закона есть
тогда
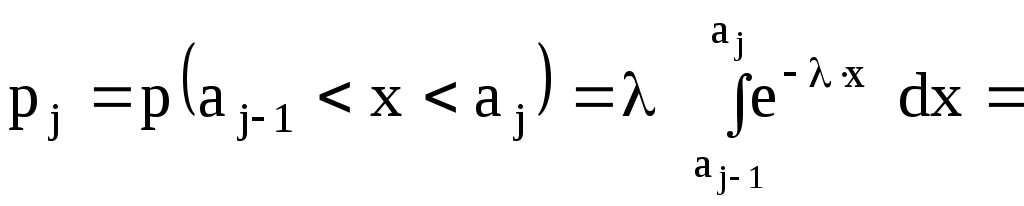
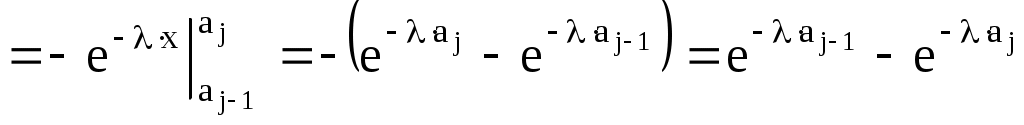 ,
,
где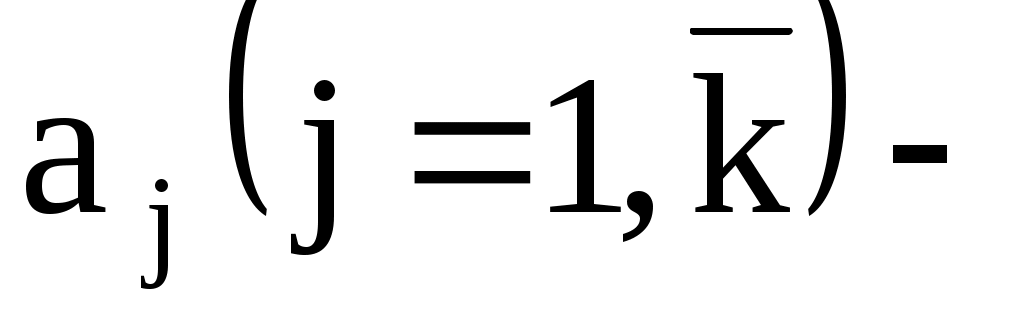 границы частичных интервалов;
границы частичных интервалов;
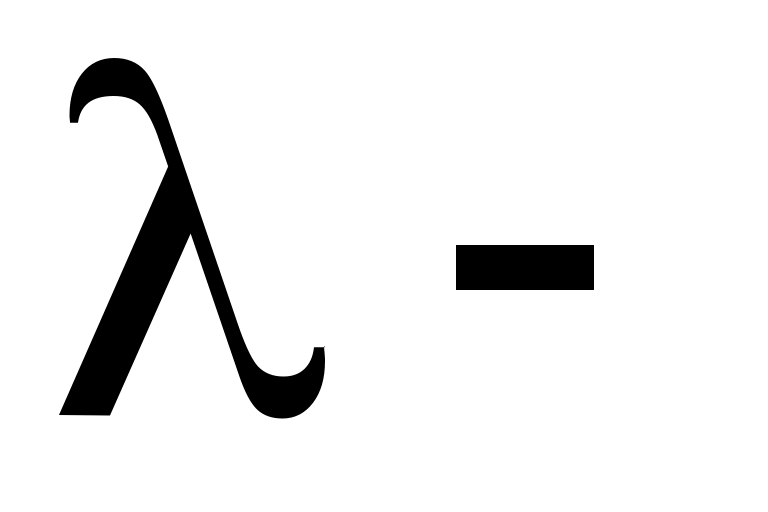 вычисляем по формуле (2.15).
вычисляем по формуле (2.15).
3. Составить сводную таблицу на основе данных табл. 2.3 и рассчитанных теоретических вероятностей (см. табл. 2.6).
4. Оценку отклонения эмпирических вероятностей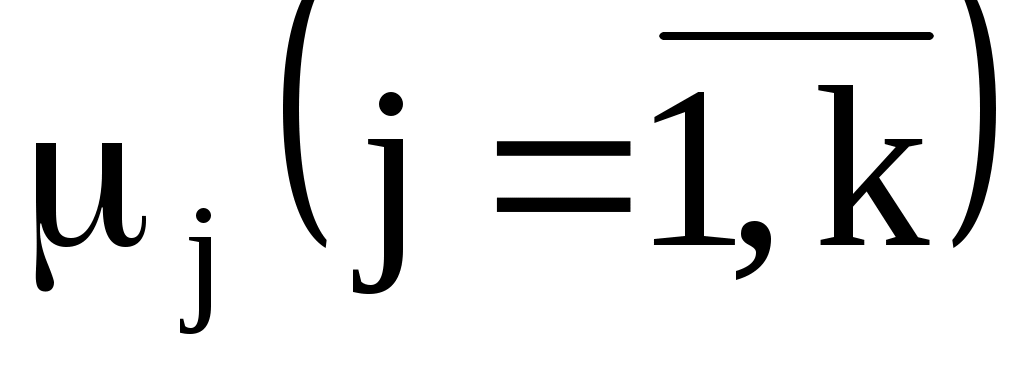 от теоретических вероятностей
от теоретических вероятностей 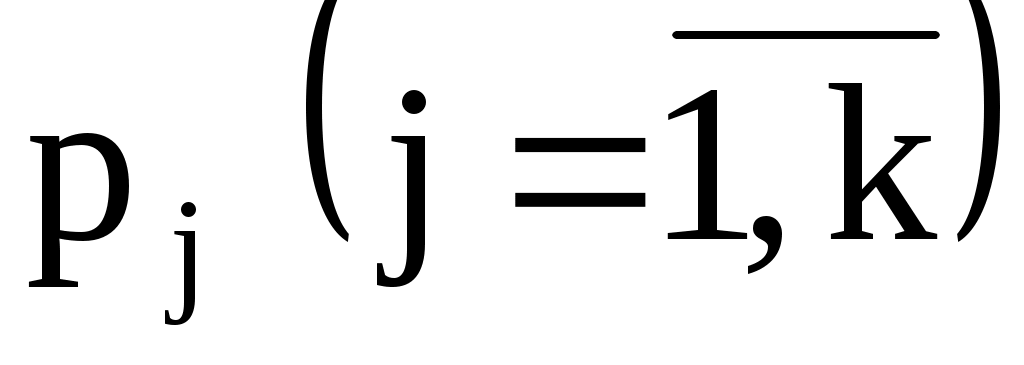 произвести с помощью критерия Пирсона
произвести с помощью критерия Пирсона  (формула (2.14)).
(формула (2.14)).
5. По таблице критических точек распределения по заданному уровню значимости
по заданному уровню значимости  и по числу степеней свободы
и по числу степеней свободы 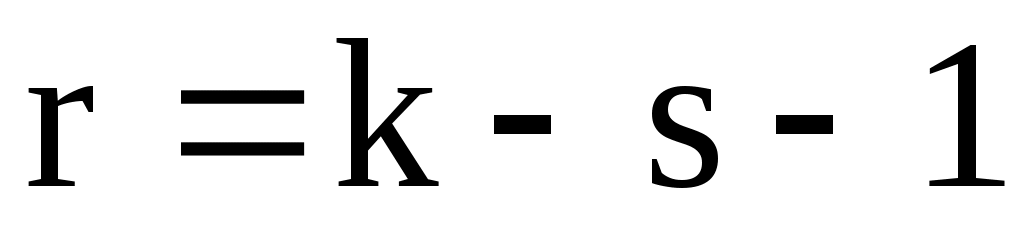 (
( количество подынтервалов,
количество подынтервалов,  - число параметров распределения,
- число параметров распределения, 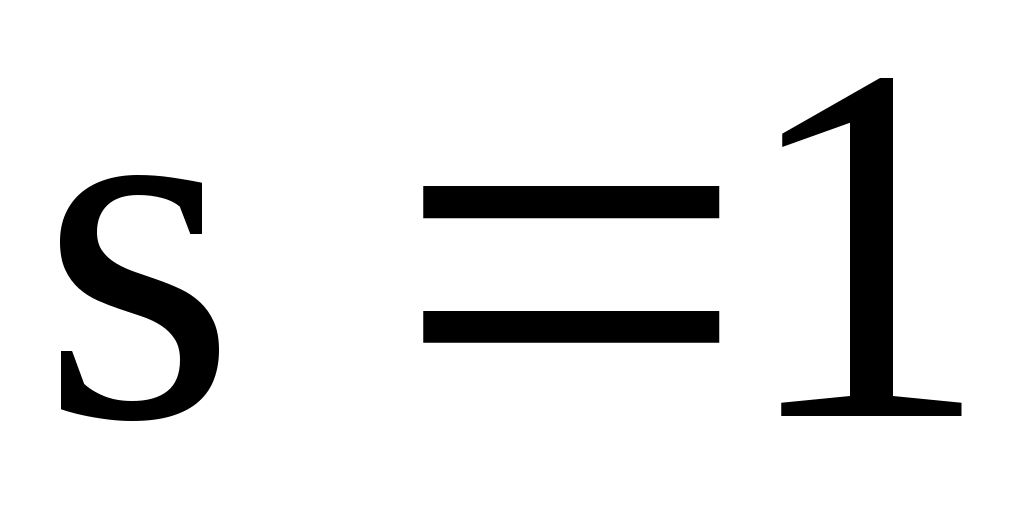 ) найти критическое значение
) найти критическое значение
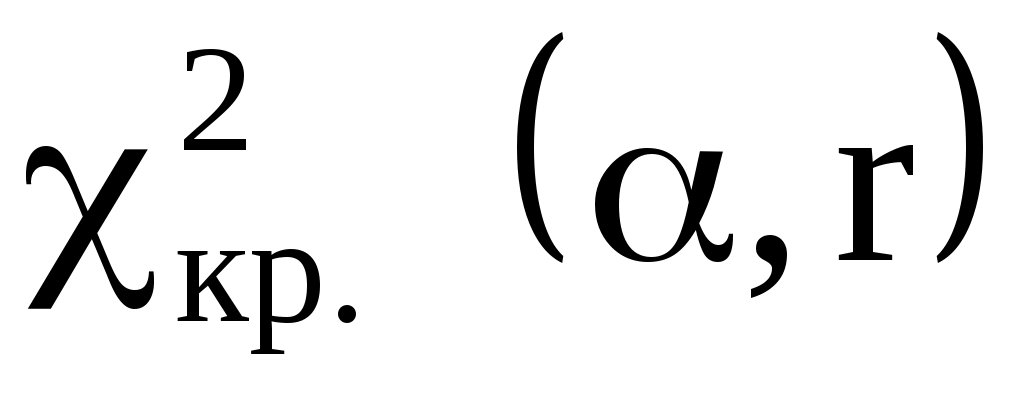 правосторонней критической области (см. Приложение 4).
правосторонней критической области (см. Приложение 4).
Далее необходимо проанализировать в соответствии с правилами 2.1 и 2.2 (для предыдущей гипотезы).
Гипотеза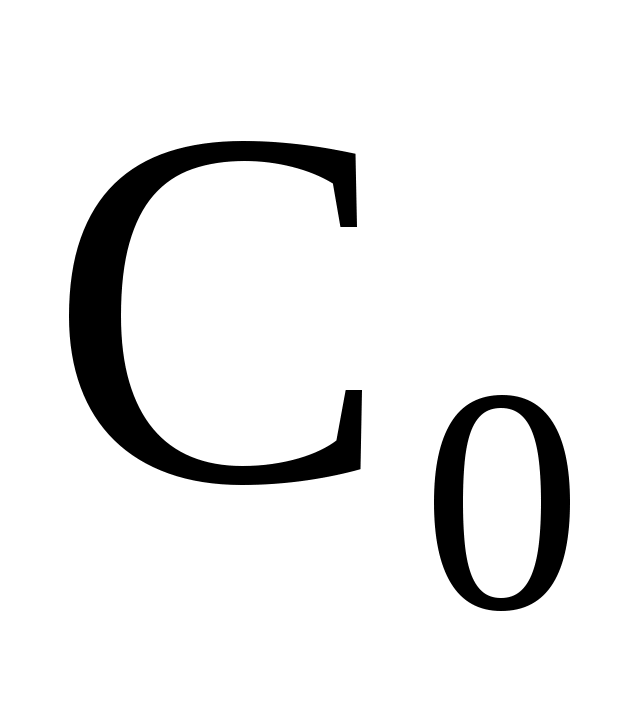 .
.
Для того, чтобы при заданном уровне значимости , проверить гипотезу о равномерном распределении генеральной совокупности надо:
, проверить гипотезу о равномерном распределении генеральной совокупности надо:
1. Оценить параметры и
и 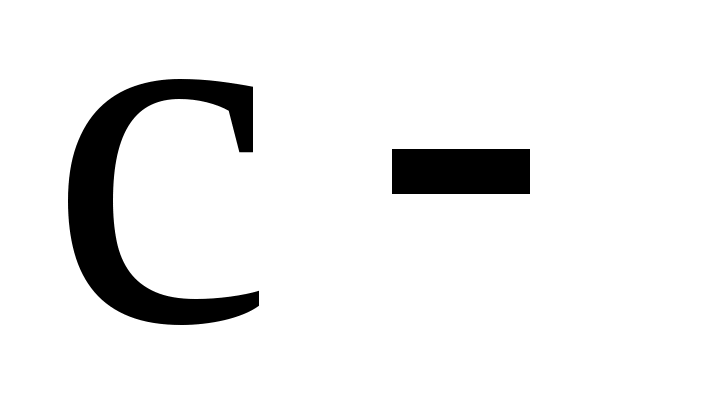 концы интервала, в котором наблюдались возможные значения
концы интервала, в котором наблюдались возможные значения 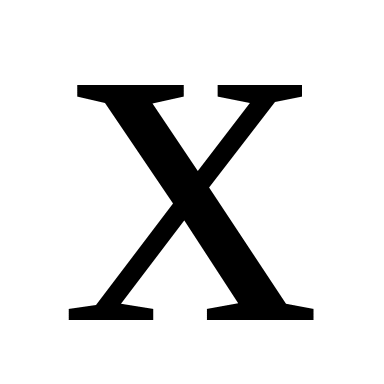 , по формулам (через
, по формулам (через  и
и  обозначены оценки параметров):
обозначены оценки параметров):
2. Вычислить теоретические частоты . Поскольку плотность распределения для равномерного закона есть
. Поскольку плотность распределения для равномерного закона есть
тогда
где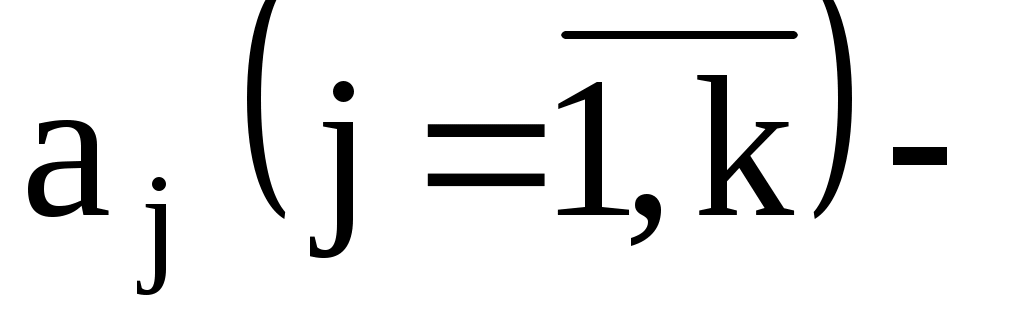 границы частичных интервалов;
границы частичных интервалов;
 длина частичных интервалов.
длина частичных интервалов.
Получаем, что все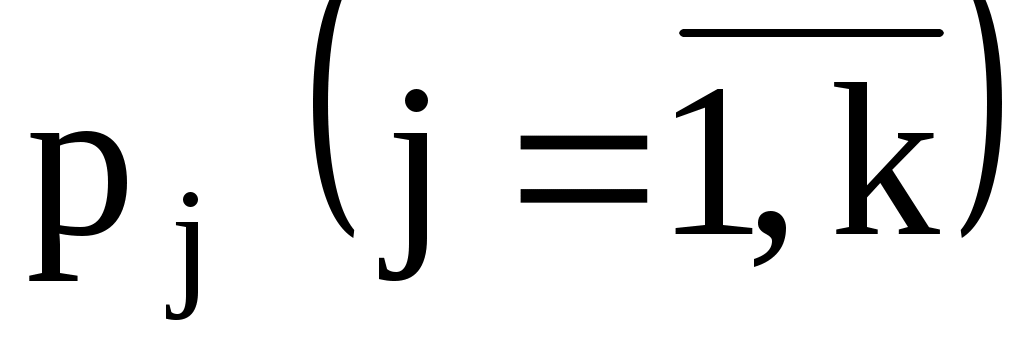 равны одному числу
равны одному числу 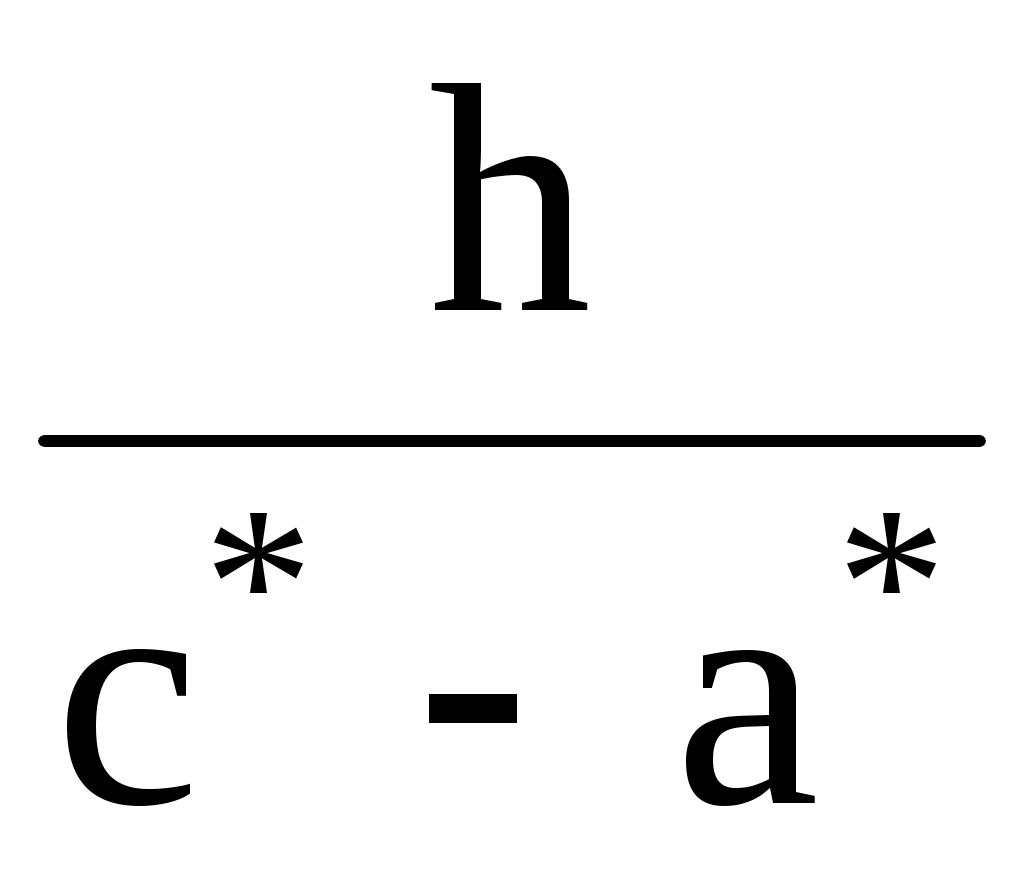 .
.
3. Составить сводную таблицу на основе эмпирических вероятностей и рассчитанных теоретических вероятностей (см. табл. 2.6).
4. Оценку отклонения эмпирических вероятностей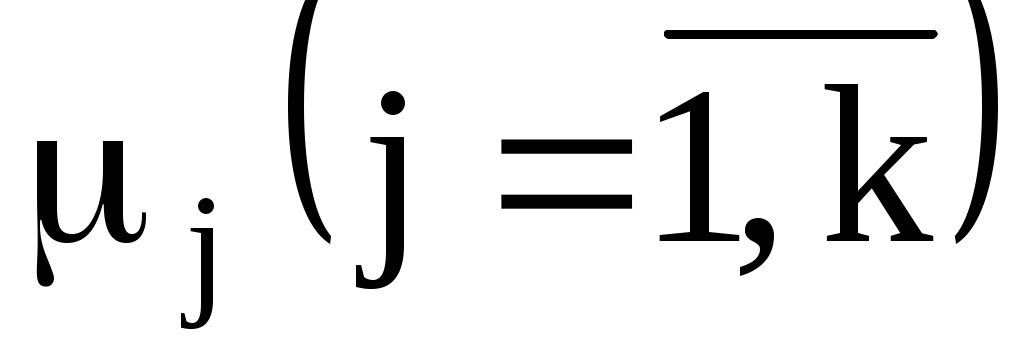 от теоретических вероятностей
от теоретических вероятностей 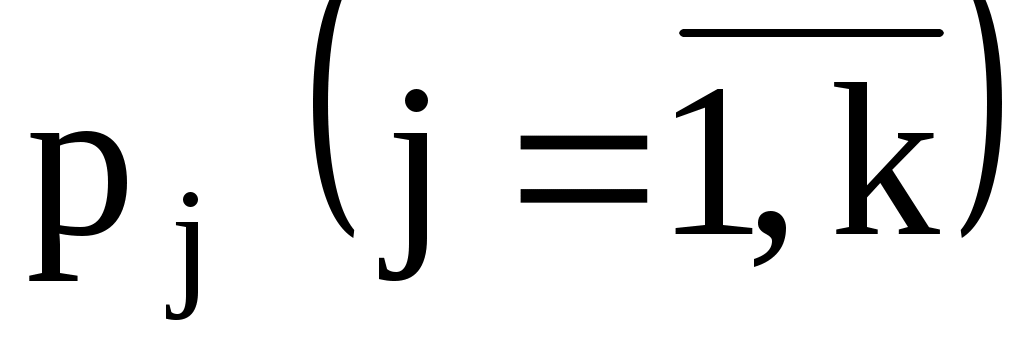 произвести с помощью критерия Пирсона
произвести с помощью критерия Пирсона 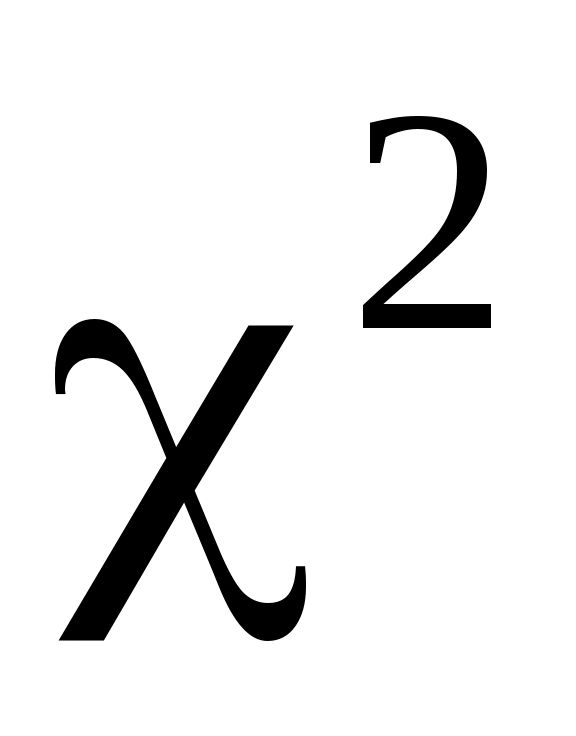 (формула (2.14)).
(формула (2.14)).
5. По таблице критических точек распределения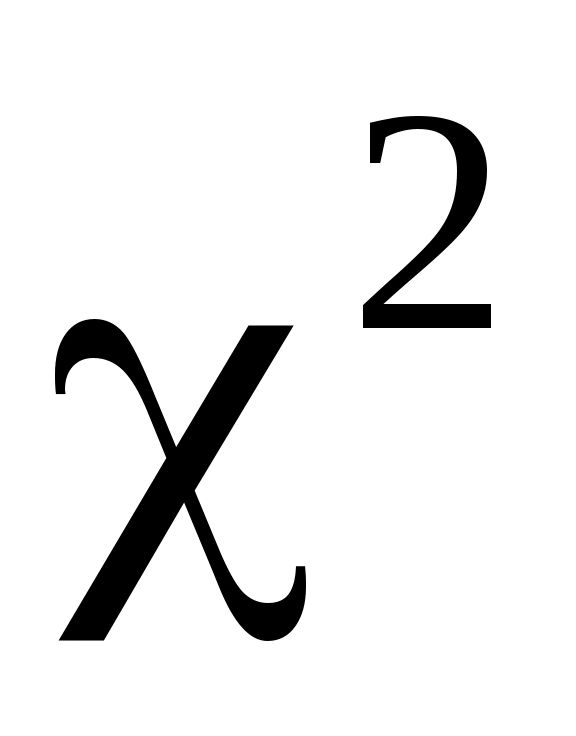 по заданному уровню значимости
по заданному уровню значимости  и по числу степеней свободы
и по числу степеней свободы 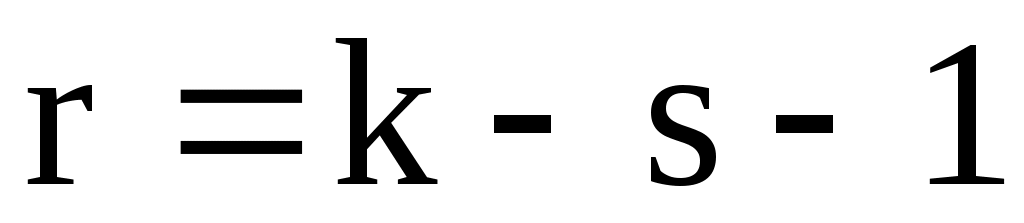 (
(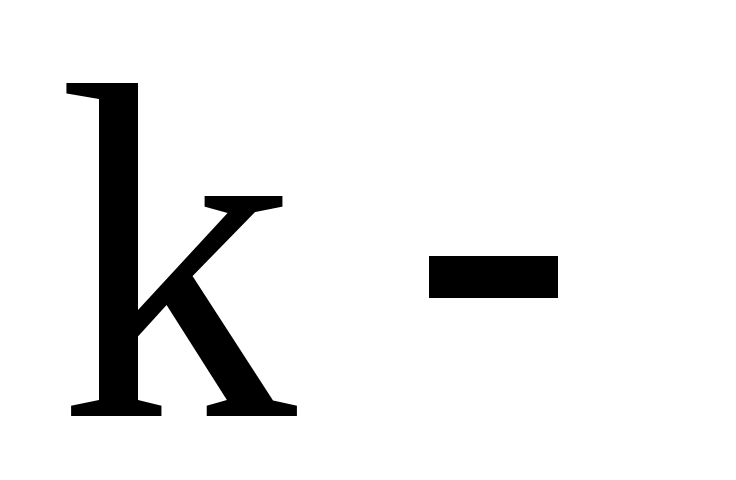 количество подынтервалов,
количество подынтервалов,  - число параметров распределений,
- число параметров распределений, 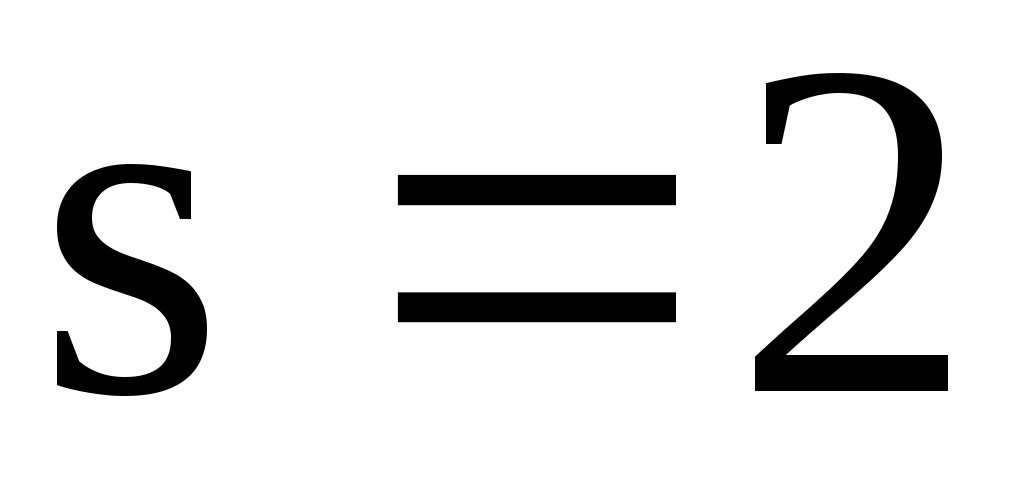 ) найти критические значения
) найти критические значения 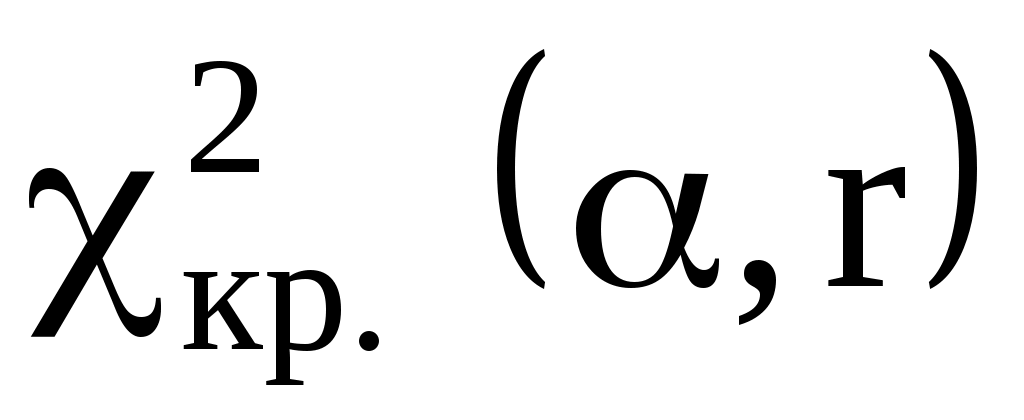 правосторонней критической области.
правосторонней критической области.
Далее анализируем в соответствии с правилами 2.1 и 2.2 (см. Гипотезу А).
Замечание 2.1. После составления таблицы 5 необходимо сделать на одном рисунке два графика: ломаную эмпирических вероятностей и кривую теоретических вероятностей.
Замечание 2.2. Здесь же на этом рисунке рекомендуется нанести:
а)
| | (2.12) |
Тогда
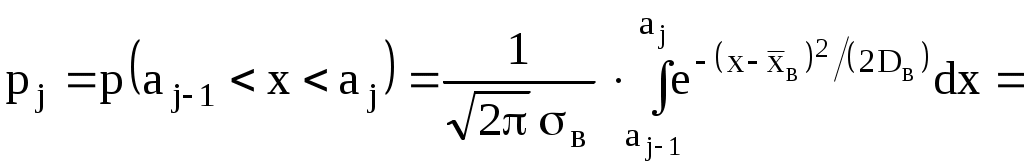 | (2.13) |
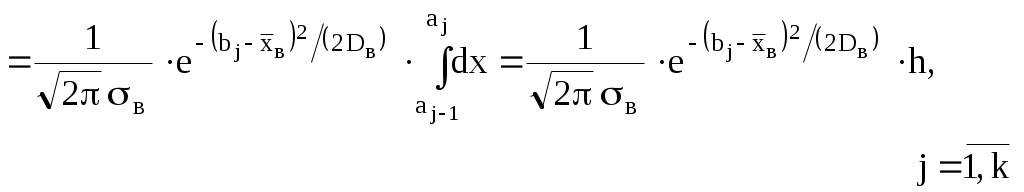 |
где
3. Составить сводную таблицу на основе данных табл. 2.3 и рассчитанных теоретических вероятностей:
Таблица 2.6
| | | | … | | … | | |
| | | | … | | … | | |
| | | | … | | … | | |
4. Оценку отклонения эмпирических вероятностей
| | (2.14) |
5. По таблице критических точек распределения
Правило 2.1. Если
Правило 2.2. Если
Гипотеза
Для того, чтобы при заданном уровне значимости
1. Вычислить
| | (2.15) |
2. Вычислить теоретические вероятности
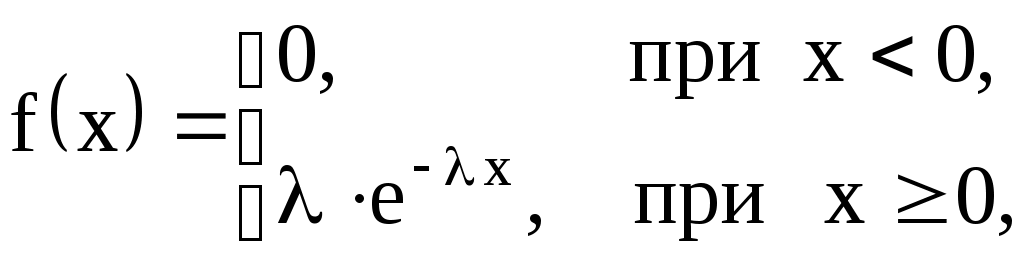 | (2.16) |
тогда
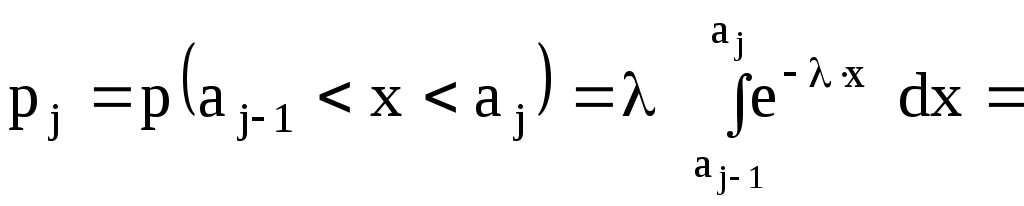
где
3. Составить сводную таблицу на основе данных табл. 2.3 и рассчитанных теоретических вероятностей (см. табл. 2.6).
4. Оценку отклонения эмпирических вероятностей
5. По таблице критических точек распределения
Далее необходимо проанализировать в соответствии с правилами 2.1 и 2.2 (для предыдущей гипотезы).
Гипотеза
Для того, чтобы при заданном уровне значимости
1. Оценить параметры
| | (2.17) |
2. Вычислить теоретические частоты
| | (2.18) |
тогда
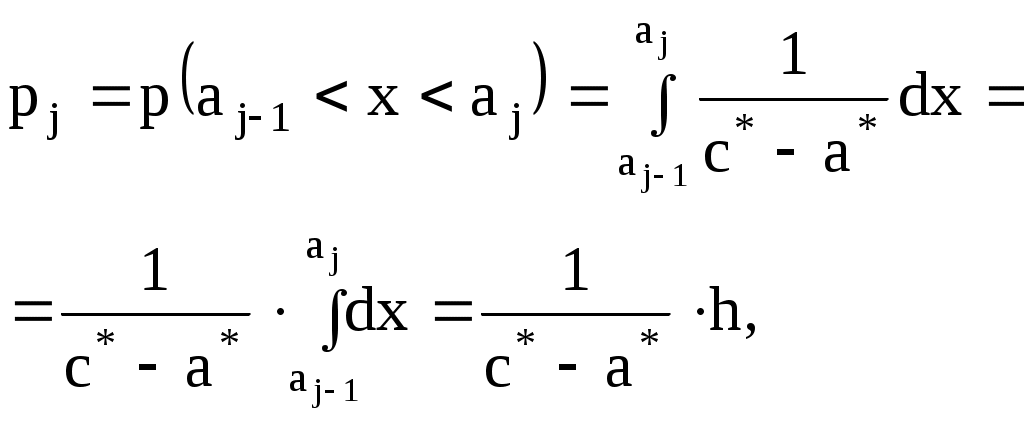 | (2.19) |
где
Получаем, что все
3. Составить сводную таблицу на основе эмпирических вероятностей и рассчитанных теоретических вероятностей (см. табл. 2.6).
4. Оценку отклонения эмпирических вероятностей
5. По таблице критических точек распределения
Далее анализируем в соответствии с правилами 2.1 и 2.2 (см. Гипотезу А).
Замечание 2.1. После составления таблицы 5 необходимо сделать на одном рисунке два графика: ломаную эмпирических вероятностей и кривую теоретических вероятностей.
Замечание 2.2. Здесь же на этом рисунке рекомендуется нанести:
а)

