Файл: Лабораторная работа 1 Первичная обработка статистических данных.doc
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 03.02.2024
Просмотров: 24
Скачиваний: 0
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
; б) доверительный интервал, построенный для одной из доверительных вероятностей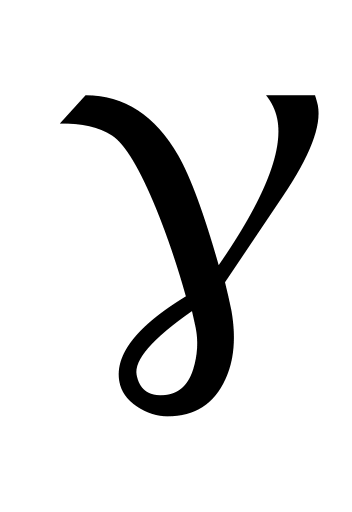 
(например, для 
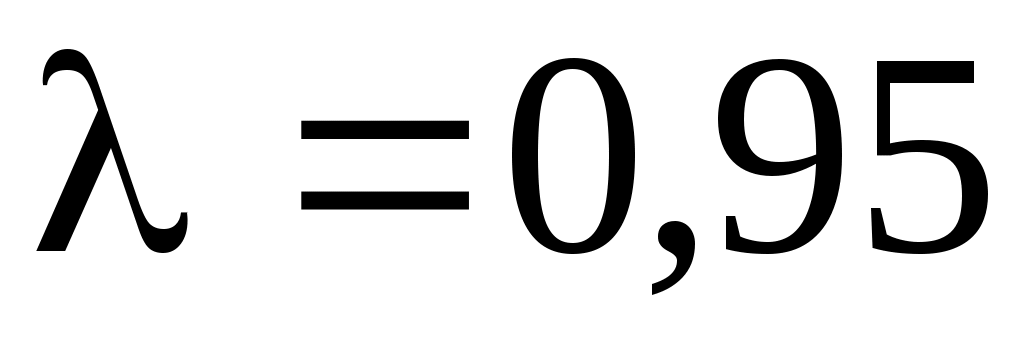); в) интервал, построенный по правилу «3-х сигм».
Замечание 2.3. Данный рисунок является наглядным результатом работы, проделанной в Л.Р. 1,2,3.
ПРИМЕР 2.3. Используя критерий согласия Пирсона при уровне значимости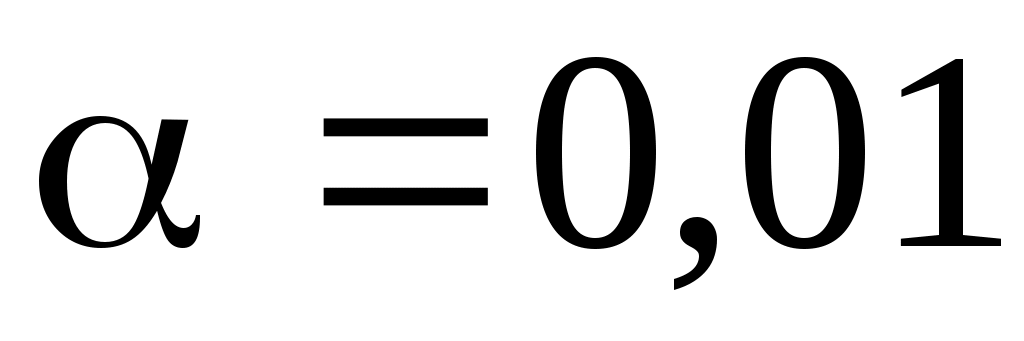
, проверить гипотезу о нормальном распределении генеральной совокупности.
1) Переносим из лабораторной работы № 1 полигон распределения относительных частот и табл. 2.5.
2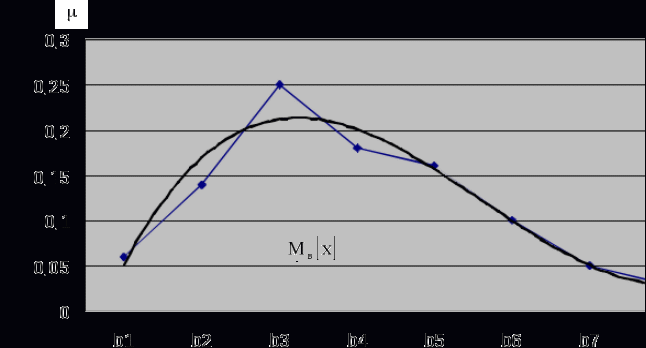
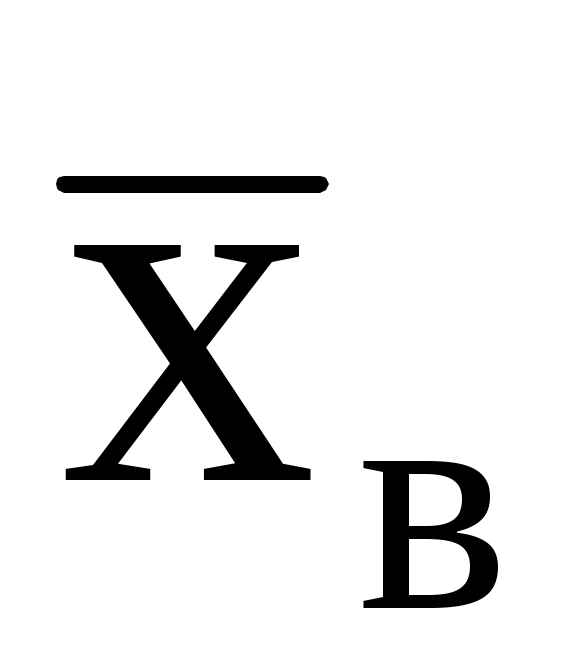
) Из визуального наблюдения ломаной делаем предположение (ставим гипотезу) о законе распределения генеральной совокупности, то есть ставим гипотезу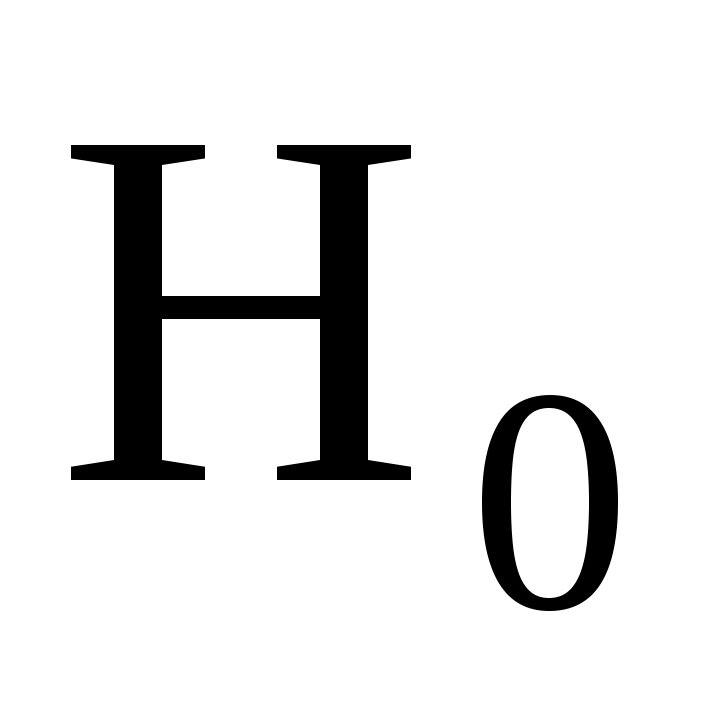
: выборка распределена по нормальному закону.
3) Вычислим теоретические вероятности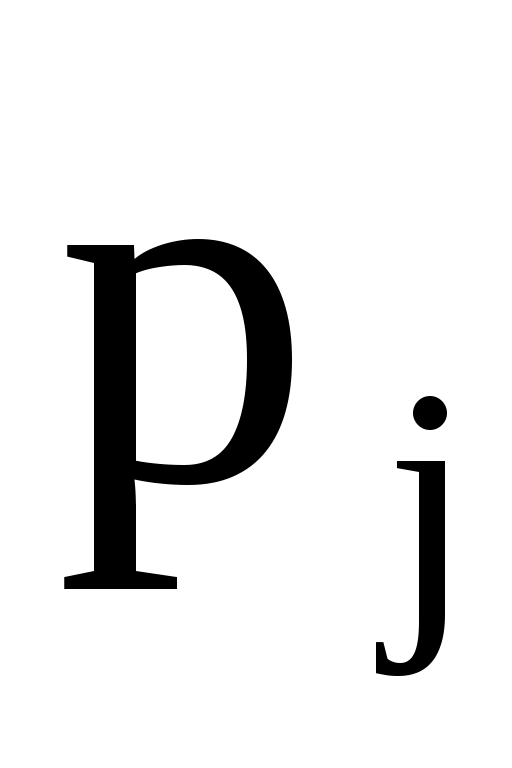
. Для этого записываем функцию плотности 
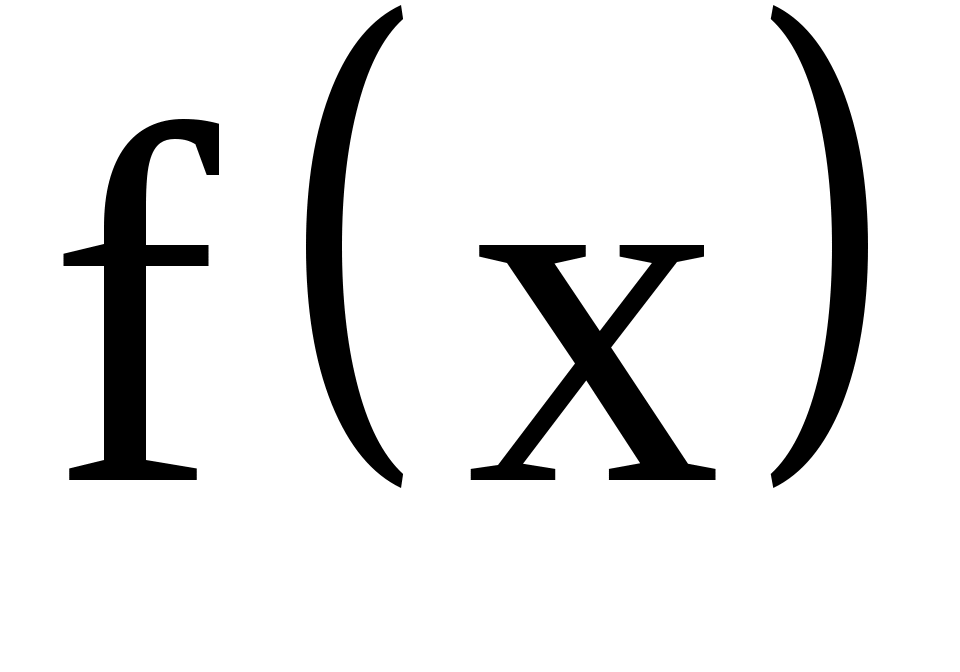для нормального закона:
.
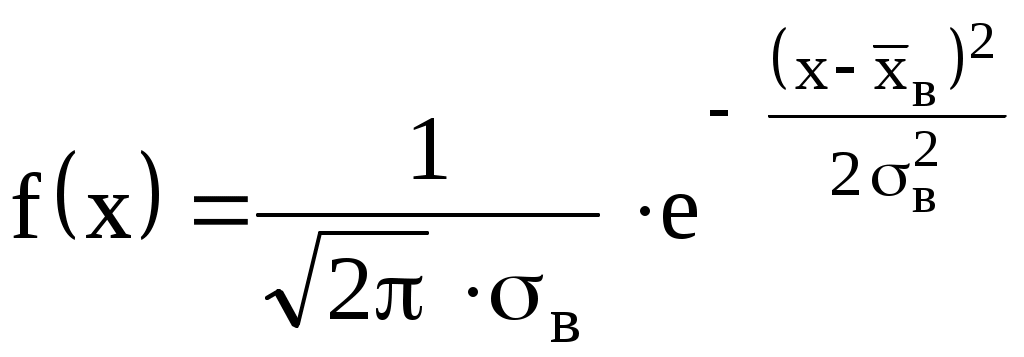Соответственно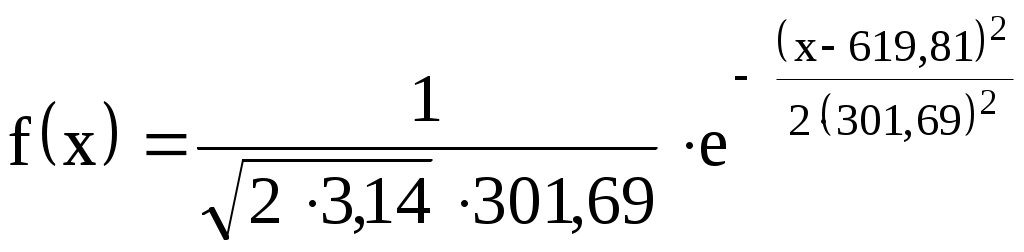
или
.
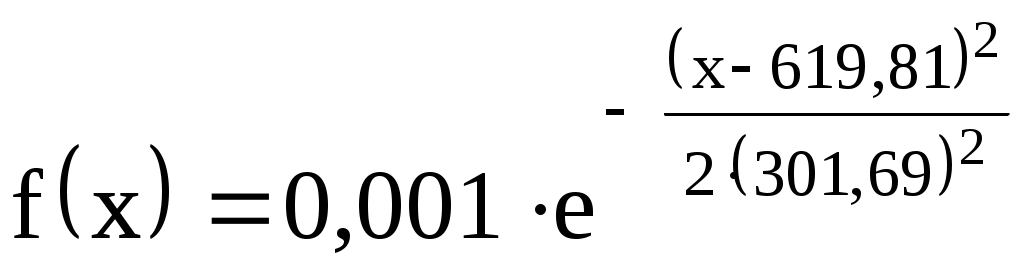Тогда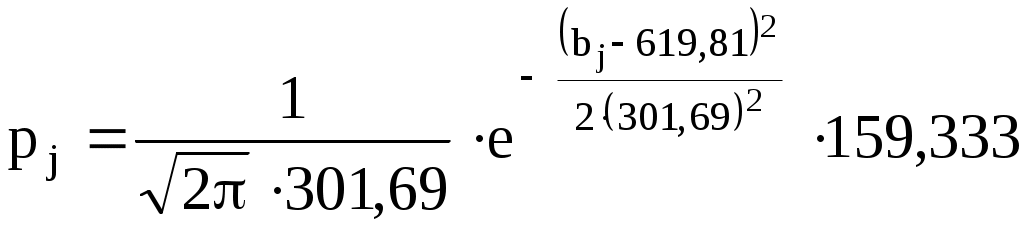
.
;
;
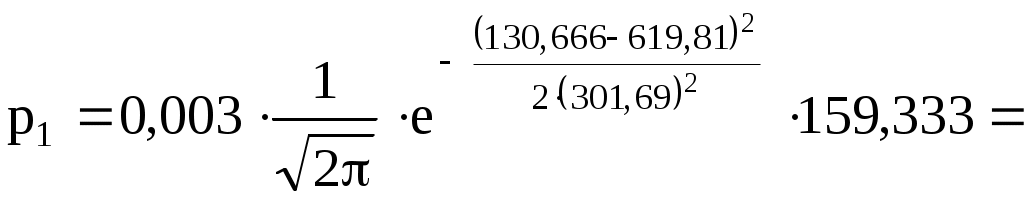
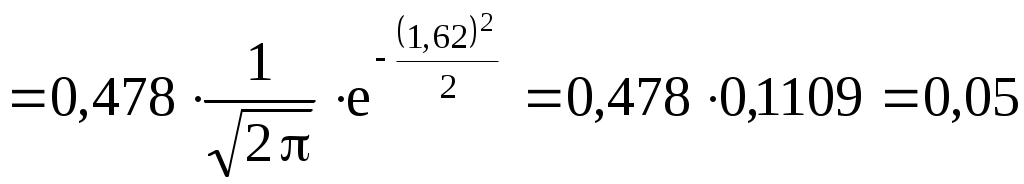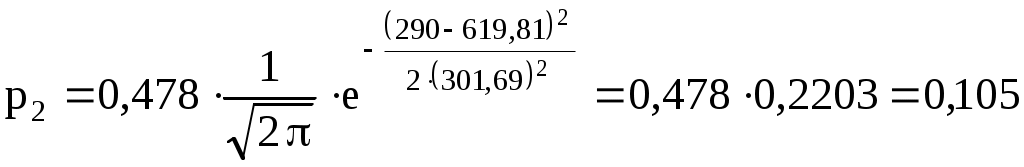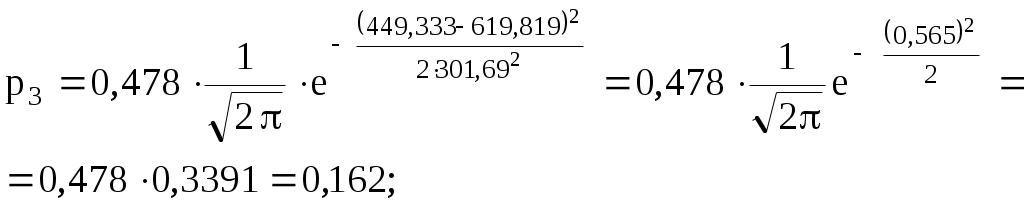
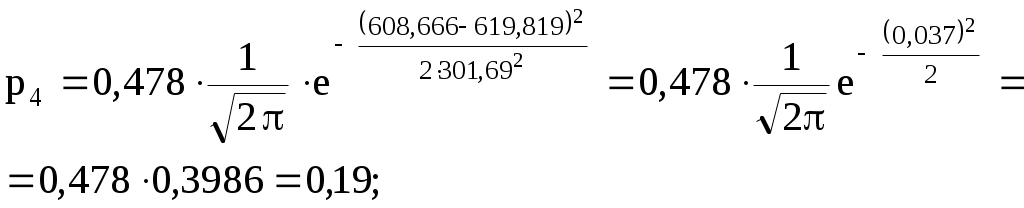
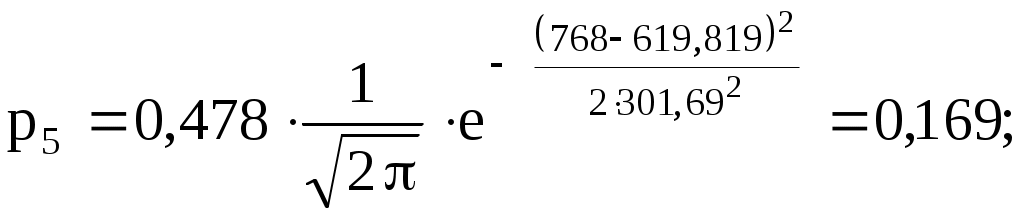
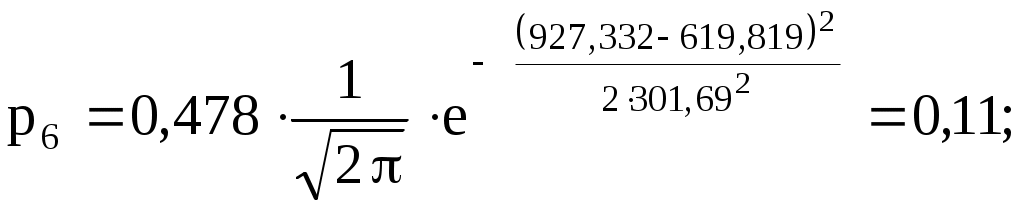
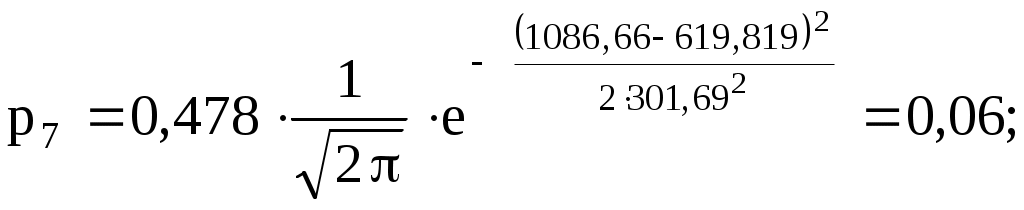
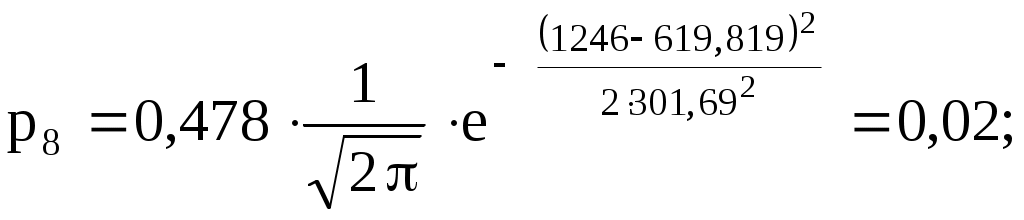
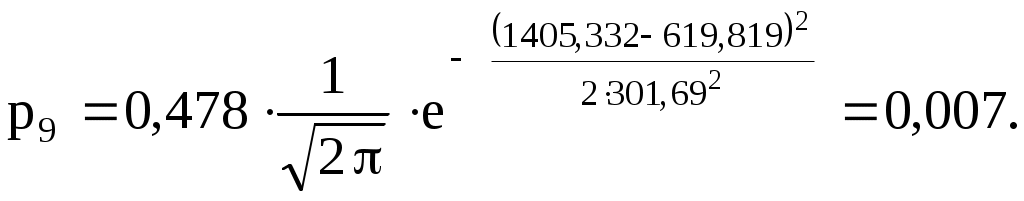
4) Составляем табл. 2.7 распределения теоретических вероятностей.
Таблица 2.7
Отметим теоретические вероятности на полигоне относительных частот.
5) Рассчитаем значение критерия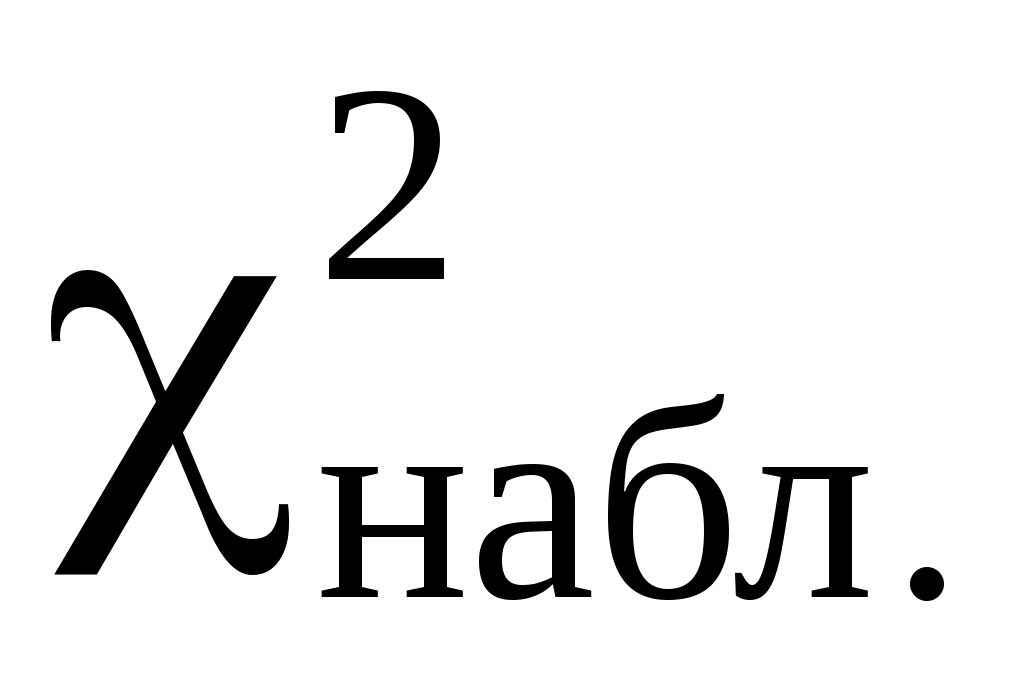
.
.
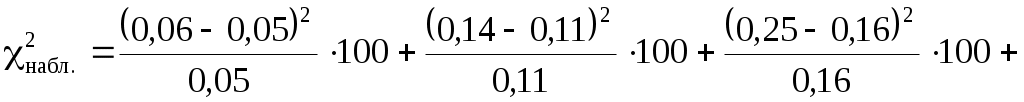
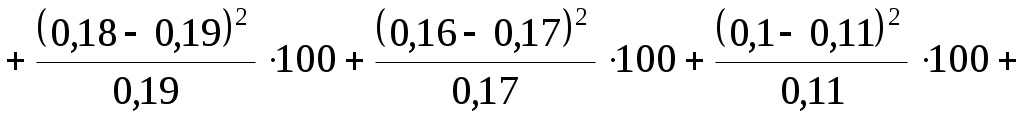
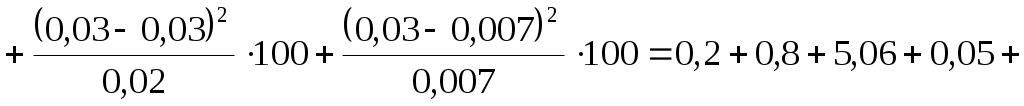
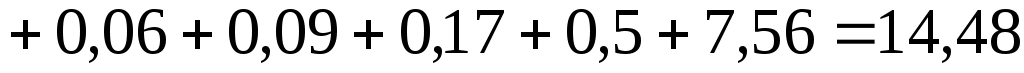6) Из таблицы «Критические точки распределения
» находим соответствующее нашим значениям 
.
. 
.
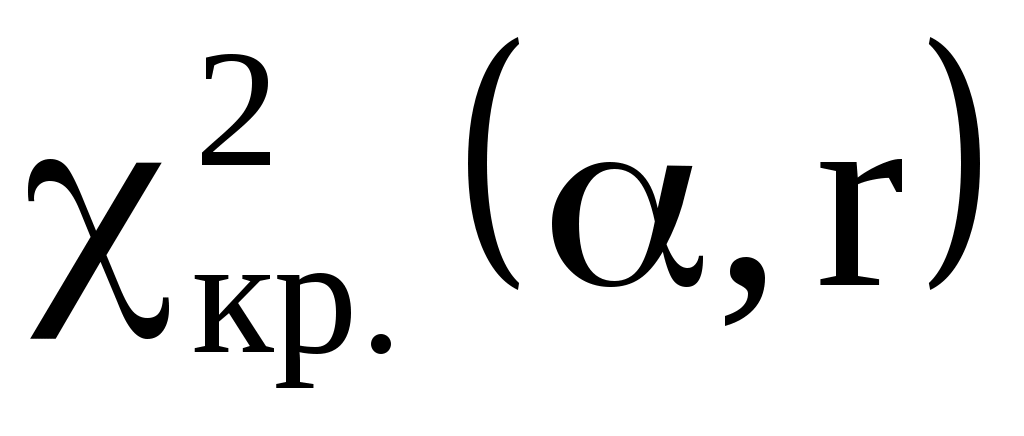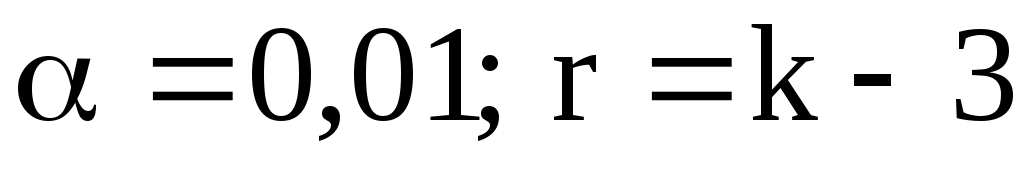
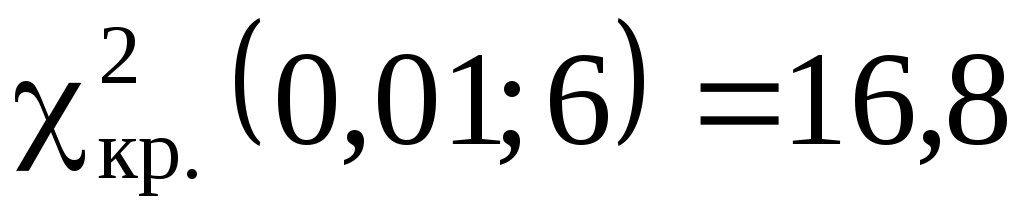Сравниваем
и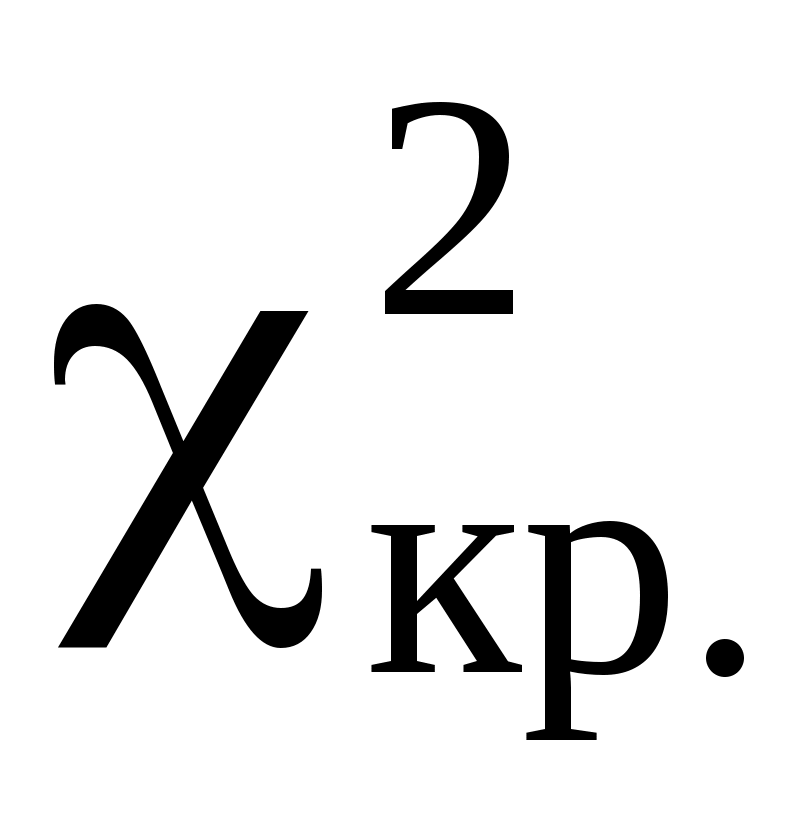 
. Так как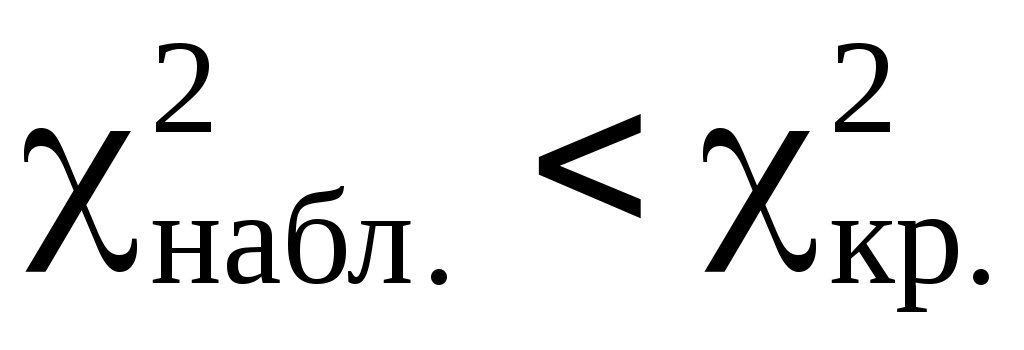 
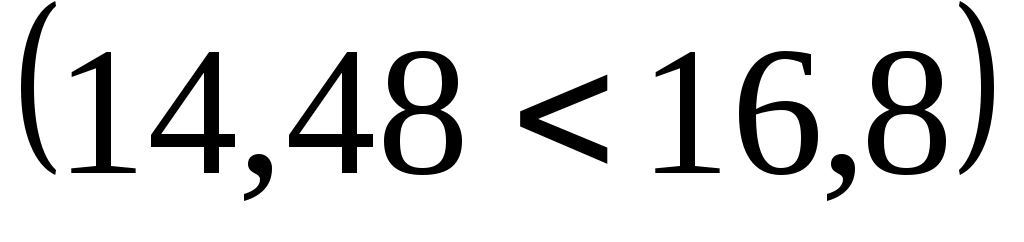, то гипотеза 
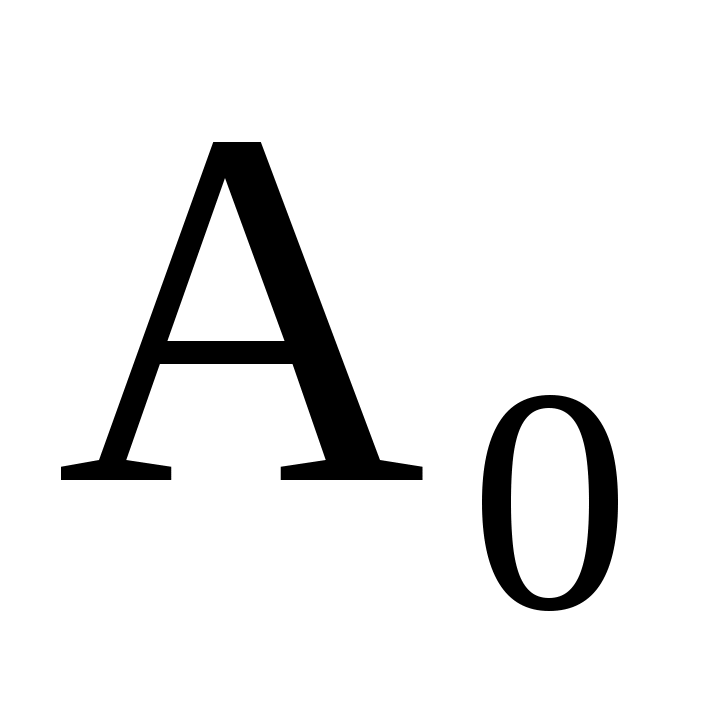(выборка распределена по нормальному закону) принимается, по правилу 2.1.
(например, для ); в) интервал, построенный по правилу «3-х сигм».Замечание 2.3. Данный рисунок является наглядным результатом работы, проделанной в Л.Р. 1,2,3.
ПРИМЕР 2.3. Используя критерий согласия Пирсона при уровне значимости
, проверить гипотезу о нормальном распределении генеральной совокупности.1) Переносим из лабораторной работы № 1 полигон распределения относительных частот и табл. 2.5.
 | 130,6 | 290 | 449,3 | 608,6 | 768 | 927,3 | 1086,6 | 1246 | 1405 |
 | 0,06 | 0,14 | 0,25 | 0,18 | 0,16 | 0,1 | 0,05 | 0,03 | 0,03 |
2
) Из визуального наблюдения ломаной делаем предположение (ставим гипотезу) о законе распределения генеральной совокупности, то есть ставим гипотезу
: выборка распределена по нормальному закону.3) Вычислим теоретические вероятности
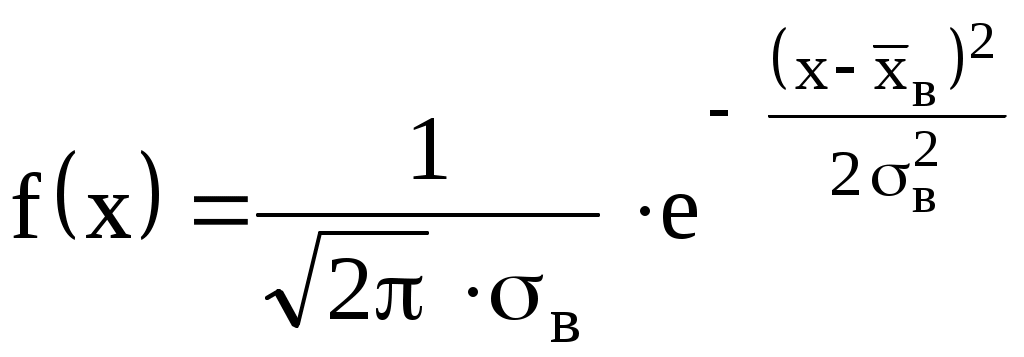. Для этого записываем функцию плотности для нормального закона: .Соответственно
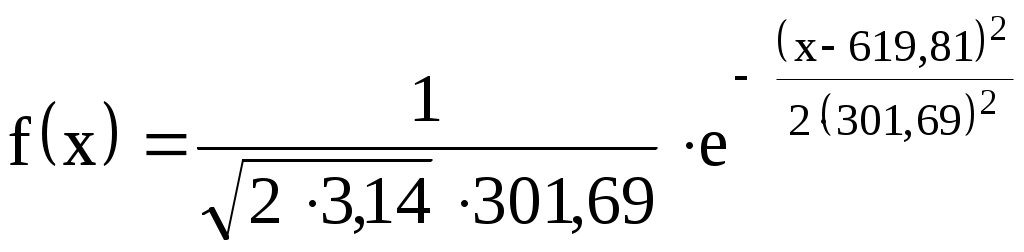
или
. Тогда
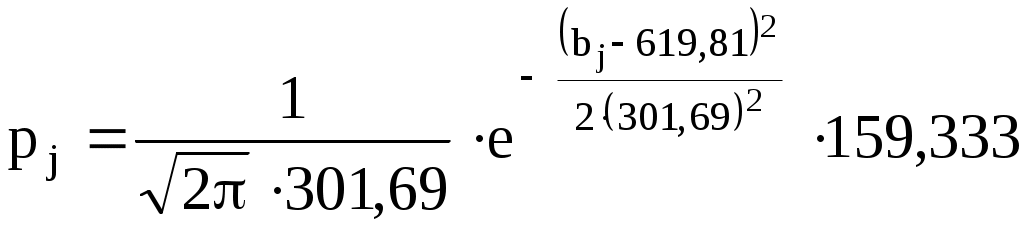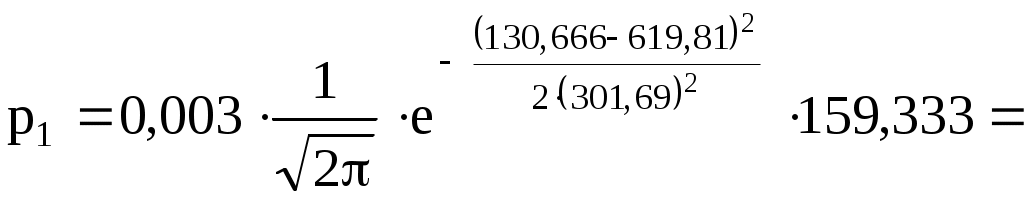
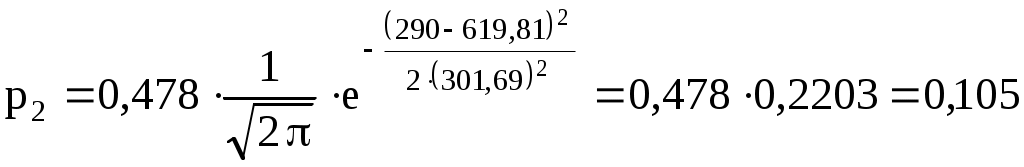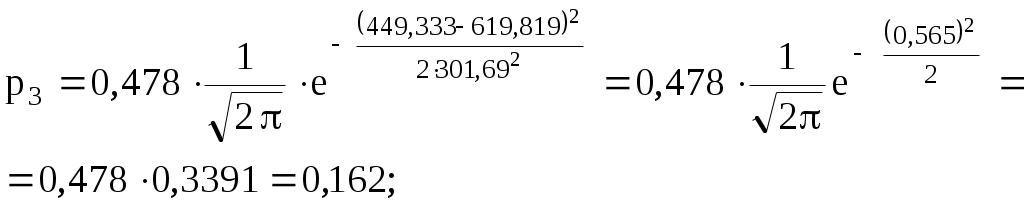
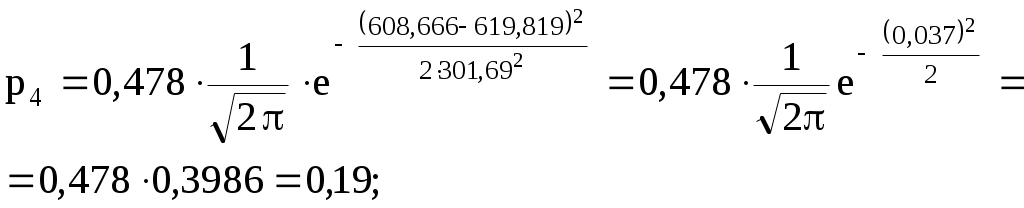
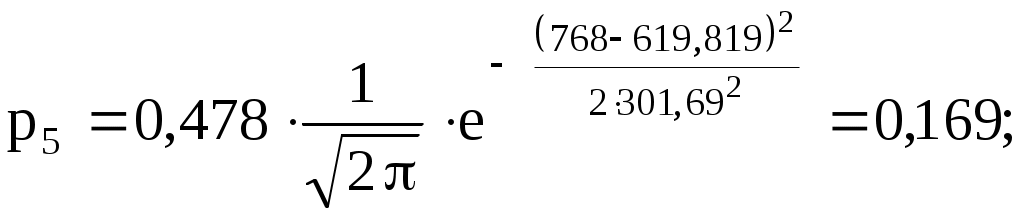
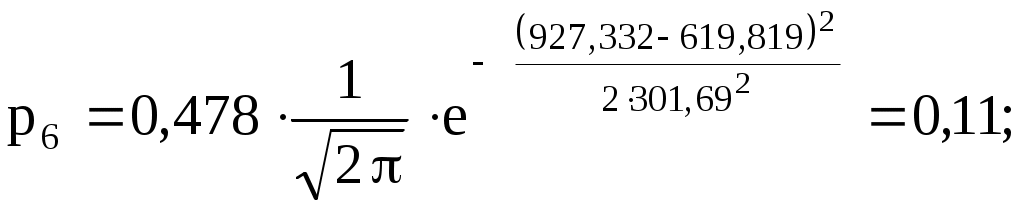
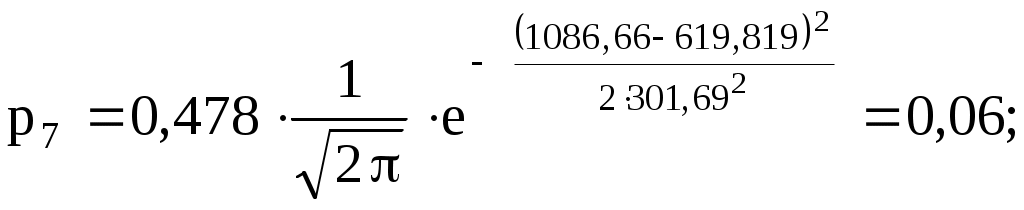
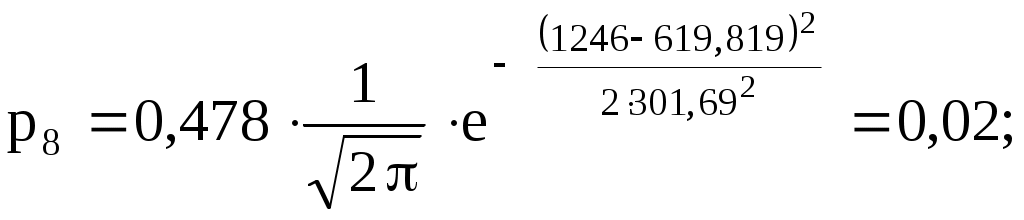
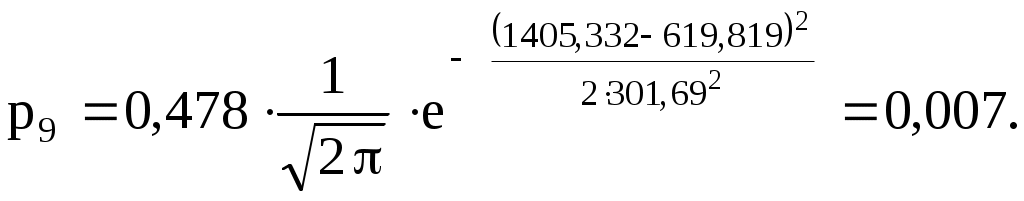
. ; ; 4) Составляем табл. 2.7 распределения теоретических вероятностей.
Таблица 2.7
| | 130,6 | 290 | 449,3 | 608,6 | 768 | 927,3 | 1086,6 | 1246 | 1405 |
 | 0,06 | 0,14 | 0,25 | 0,18 | 0,16 | 0,1 | 0,05 | 0,03 | 0,03 |
 | 0,05 | 0,105 | 0,162 | 0,19 | 0,17 | 0,11 | 0,06 | 0,02 | 0,007 |
Отметим теоретические вероятности на полигоне относительных частот.
5) Рассчитаем значение критерия
.
.6) Из таблицы «Критические точки распределения
» находим соответствующее нашим значениям . . .Сравниваем
и . Так как , то гипотеза (выборка распределена по нормальному закону) принимается, по правилу 2.1.