Файл: Лабораторная работа 1 Первичная обработка статистических данных.doc

Скачать файл (0,75Мб)

Заказать решение

ВУЗ: Не указан

Категория: Не указан

Дисциплина: Не указана

Добавлен: 03.02.2024

Просмотров: 23

Скачиваний: 0

ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.

которую считаем по данным таблицы 2.3.

Смещенной оценкой генеральной дисперсии

служит выборочная дисперсия:

(2.6)

где

из таблицы 2.3. Иногда более удобно пользоваться другой формулой для вычисления выборочной дисперсии:

(2.6а)

Замечание. Поскольку

является смещенной оценкой, то ее «исправляют» следующим образом:

(2.7)

Полученная оценка

это несмещенная дисперсия, а

выборочное среднее квадратическое отклонение.

При выборке малого объема точечная оценка может значительно отличаться от оцениваемого генерального параметра, то есть приводит к грубым ошибкам, поэтому при небольшом объеме выборки следует пользоваться интервальными оценками.

Интервальной называют оценку, которая определяется двумя числами – концами интервала, покрывающего оцениваемый генеральный параметр

.

Доверительным называют интервал, который с заданной надежностью (доверительной вероятностью)

покрывает оцениваемый генеральный параметр, то есть с которой осуществляется неравенство

.

Обычно надежность оценки (доверительная вероятность

) задается. Причем в качестве

берут число, близкое к единице (0,95; 0,99; 0,999).

Итак, пусть вероятность того, что

равна

, то есть

(2.8)

или

(2.8а)

тогда интервал

и есть доверительный интервал.

Для оценки математического ожидания

нормально распределенной генеральной совокупности

по выборочной средней

при известном среднем квадратическом отклонении

служит доверительный интервал.

(2.9)

где

точность оценки;

объем выборки;

это такое значение аргумента функции Лапласа

(приложение 1), при котором

.
Для оценки математического ожидания нормально распределенной генеральной совокупности

по выборочной средней

при неизвестном среднем квадратическом отклонении

и (при объеме выборки

) служит доверительный интервал

(2.10)

где

находим по таблице (приложение 2) по заданным

.

Для оценки среднего квадратического отклонения

нормально распределенной генеральной совокупности

с доверительной вероятностью служат доверительные интервалы:

(2.11)

где

находим по таблице (приложение 3) при заданных

.

Замечание. Для m предлагается построить доверительные интервалы для двух значений вероятности

. Провести анализ, как меняются границы интервалов с увеличением доверительной вероятности.

ПРИМЕР 2.2. Найти точечные и интервальные оценки генерального математического ожидания и генеральной дисперсии, исходя из данных примера 2.1.

1) По данным таблицы 2.5 рассчитываем выборочное математическое ожидание и выборочную дисперсию, среднее квадратическое отклонение.

.

По данным табл. 2.4 вычисляем еще одну точечную характеристику среднее арифметическое значение нашей выборки

.

2) Делаем расчет интервальных оценок, то есть будем строить доверительные интервалы с доверительной вероятностью

.

а)

Ищем соответствующее значение

по таблице в приложении 2

.

Точность оценки

. Тогда

;

.

б)

;

.

Строим полученные интервалы на полигоне распределения относительных частот.

2

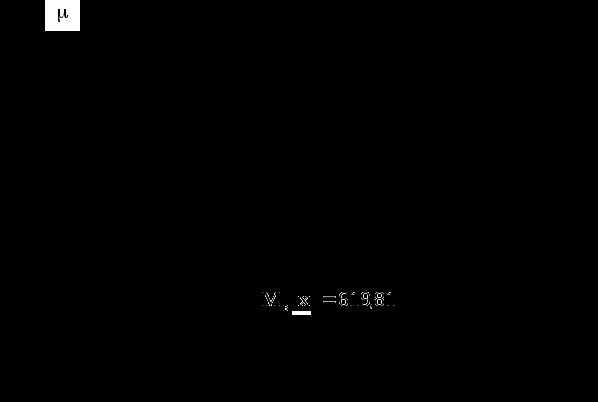
.3 Лабораторная работа № 3

«Проверка гипотезы о законе распределения генеральной совокупности».
В лабораторной работе №1 в результате первичной обработки исходных данных получено эмпирическое распределение (табл. 2.3) и по данным этой таблицы построен полигон относительных частот. Относительные частоты иногда называют эмпирическими вероятностями. Из визуального наблюдения полигона можно сделать один из следующих выводов:

Гипотеза : Генеральная совокупность распределена по нормальному закону;

Гипотеза : Генеральная совокупность распределена по

показательному закону;

Гипотеза : Генеральная совокупность распределена по равномерному закону.

Гипотеза .

Для того, чтобы при заданном уровне значимости