ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 03.02.2024
Просмотров: 22
Скачиваний: 0
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Вопросы к зачету (закрепление компетенций ОПК-4 ПК- 2 ПК-8):
1. Группировка исходных данных в ППП Statistica.
ППП STATISTICA – это универсальная интегрированная система, предназначенная для статистического анализа и обработки данных. Содержит многофункциональную систему для работы с данными, широкий набор статистических модулей, в которых собраны группы логически связанных между собой статистических процедур, специальный инструментарий для подготовки отчетов, мощную графическую систему для визуализации данных, систему обмена данными с другими Windows-приложениями.
Группировка, в которой для характеристики групп применяется численность группы, называется рядом распределения. Ряд распределения состоит из двух элементов: варианты – отдельного значения варьирующего признака, которое он принимает в ряду распределения, и частоты – численность отдельных вариант, т.е. частота повторения каждой варианты. Если частота выражена в долях единицы или в процентах к итогу (к общей сумме частот), то это – частость.
В пакете STATISTICA широкие возможности по проведению группировки, построению рядов распределения и их графиков предоставляют Frequency tables – Таблицы частот и Tables andbanners -Таблицы и заголовки в меню Analysis-Анализ модуля Basic Statistics and Tables – Основные статистики и таблицы.
2. Непараметрические методы оценки тесноты связи в ППП Statistica.
Непараметрические методы статистики – это методы, независящие от характера распределения генеральной совокупности. Этим они отличаются от параметрических методов, к которым относят, например, корреляционно-регрессионный анализ. Именно отсутствие требования о знании закона распределения исследуемых показателей делают непараметрические методы особенно привлекательными и популярными в «западной» статистике.
Пакет STATISTICA через диалоговое окно NonparametricStatistics предлагает следующие процедуры:
2x2 Tables–выявление связи между двумя качественными альтернативными признаками. ObservedversusexpectedXi – проверка согласия наблюдаемых и ожидаемых частот. Ожидаемые частоты – это частоты, вычисленные на основе предполагаемого закона распределения случайной величины.
Correlations – выявление связи между двумя количественными признаками (коэффициенты ранговой корреляции Спирмена и Кендэла, гамма-коэффициент). Comparingtwoindependentsamples – проверка гипотезы о том, что две группы данных представляют собой случайные независимые выборки из одной генеральной совокупности и имеют равные средние и медианы. Предлагаются критерий серий Вальда Вольфовица (Wald-Wolfowitzrunstest), двухвыборочный тест Колмогорова-Смирного (Kolmogorov-Smirnovtwo-sampetest), критерий Манна-Уитни (Mann-WhitneyUtest).
Comparingmultipleindep. samples – проверка гипотезы о том, что несколько выборок получены из одной генеральной совокупности. Используется критерий Краскела-Уоллиса (Summary: Kruskal-WallisANOVA).
Comparingtwodependentsamples – проверка гипотезы об однородности генеральных совокупностей попарно связанным выборкам (например, сравнение работы двух одинаковых приборов). Предлагаются критерий знаков (Signtest) и критерий Вилкоксона (Wilcoxonwatchedpairtest).
Comparingmultipledep. samples – двухфакторный анализ Фридмана и коэффициент конкордации Кендэла (Summary: Friedman ANOVA; Kendall'sconcordance). Проверяется гипотеза о том, что связанные выборки принадлежат однородным генеральным совокупностям. Коэффициент конкордацииКендэла показывает меру связи. Широко используется при оценке согласованности мнений экспертов.
CochranQtest – Q-критерий Кохрена используется для анализа связанных выборок, содержащих значения качественного альтернативного признака.
3. Проведение многомерной группировки методом кластерного анализа в среде ППП Statistica.
В программе STATISTICA реализованы агломеративные методы минимальной дисперсии – древовидная кластеризация и двухвходовая кластеризация, а также дивизивный метод k-средних.
В методе древовидной кластеризации предусмотрены различные правила иерархического объединения в кластеры
1. Правило одиночной связи. На первом шаге объединяются два наиболее близких объекта, т.е. имеющие максимальную меру сходства. На следующем шаге к ним присоединяется объект с максимальной мерой сходства с одним из объектов кластера, т.е. для его включения в кластер требуется максимальное сходство лишь с одним членом кластера. Метод называют еще методом ближайшего соседа, так как расстояние между двумя кластерами определяется как расстояние между двумя наиболее близкими объектами в различных кластерах. Это правило «нанизывает» объекты для формирования кластеров. Недостаток данного метода – образование слишком больших продолговатых кластеров.
2. Правило полных связей. Метод позволяет устранить недостаток, присущий методу одиночной связи. Суть правила в том, что два объекта, принадлежащих одной и той же группе (кластеру), имеют коэффициент сходства, который больше некоторого порогового значения S. В терминах евклидова расстояния это означает, что расстояние между двумя точками (объектами) кластера не должно превышать некоторого порогового значения d. Таким образом, d определяет максимально допустимый диаметр подмножества, образующего кластер. Этот метод называют еще
методом наиболее удаленных соседей, так как при достаточно большом пороговом значении d расстояние между кластерами определяется наибольшим расстоянием между любыми двумя объектами в различных кластерах.
3. Правило невзвешенного попарного среднего. Расстояние между двумя кластерами определяется как среднее расстояние между всеми парами объектов в них. Метод эффективен, когда объекты в действительности формируют различные группы, однако он работает одинаково хорошо и в случаях протяженных (цепочного типа) кластеров.
4. Правило взвешенное попарное среднее. Метод идентичен предыдущему, за исключением того, что при вычислении размер соответствующих кластеров используется в качестве весового коэффициента. Желательно этот метод использовать, когда предполагаются неравные размеры кластеров.
5. Невзвешенный центроидный метод. Расстояние между двумя кластерами определяется как расстояние между их центрами тяжести.
6. Взвешенный центроидный метод. Идентичен предыдущему, за исключением того, что при вычислениях расстояния используют веса для учета разности между размерами кластеров. Поэтому, если имеются (или подозреваются) значительные отличия в размерах кластеров, этот метод оказывается предпочтительнее предыдущего.
7. Правило Уорда (Варда). В этом методе в качестве целевой функции применяют внуригрупповую сумму квадратов отклонений, которая есть не что иное, как сумма квадратов расстояний между каждой точкой (объектом) и средней по кластеру, содержащему этот объект. На каждом шаге объединяются такие два кластера, которые приводят к минимальному увеличению целевой функции, т.е. внутригрупповой суммы квадратов отклонений. Этот метод направлен на объединение близко расположенных кластеров. Замечено, что метод Уорда приводит к образованию кластеров примерно равных размеров и имеющих форму гиперсфер.
4. Наивные модели прогнозирования.
«Наивная» модель прогнозирования предполагает, что последний период прогнозируемого временного ряда лучше всего описывает будущее этого ряда. В таких моделях прогноз, как правило, является довольно простой функцией от наблюдений прогнозируемой величины в недалеком прошлом. Простейшая модель описывается выражением:
y(t+1)=y(t),
где y(t) - последнее наблюдаемое значение, y(t+1) - прогноз. Данная модель не только не учитывает закономерности прогнозируемого процесса (что в той или мной степени свойственно многим статистическим методам прогнозирования), но и не защищена от случайных изменений в данных, а также не отражает сезонные колебания частоты и тренды.5. Оценивание и анализ парной линейной регрессии.
Парная линейная регрессия описывается уравнением:
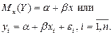
Для получения оценки параметров линейной функции регрессии взята выборка, состоящая из векторных переменных (xi, yi).
Оценкой записанной выше модели является уравнение
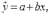где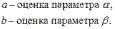
Классический подход к оцениванию параметров α и β основан на классическом (обычном или традиционном) методе наименьших квадратов (МНК).
Чтобы регрессионный анализ давал достоверные результаты необходимо выполнить 4условия Гаусса - Маркова:
1. M(εi) = 0 – остатки имеют нулевое среднее для всех i = 1,…, n.
2. D(εi) = σ2 = const для всех i = 1,…, n – гомоскедастичность остатков, то есть их равноизменчивость.
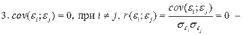
– отсутствие автокорреляции в остатках.
4. Объясняющая переменная X детерминирована, а объясняемая переменная Y – случайная величина и остатки не коррелируют с X:
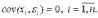
Объясняющая переменная в том случае, когда она стоит в уравнении регрессии, может называться регрессором.
Наряду с этими четырьмя условиями Гаусса - Маркова применяют 5-е условие: остатки должны быть распределены нормально; это условие необходимо для обеспечения правильного оценивания значимости уравнения регрессии и его параметров.
Наилучшие оценки называют BLUE – оценками (Best Linear Unbiased Estimators).
Они обладают следующими свойствами:
1. Это оценки несмещённые:
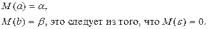
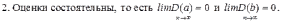
3. Оценки эффективны, то есть имеют наименьшие дисперсии среди всех возможных оценок.
Если нарушаются 2-е и/или 3-е условия Гаусса – Маркова, то оценки не теряют свойства 1и 2, а свойство 3 (эффективность) теряют; дисперсии становятся смещёнными.
6. Оценивание и анализ парной нелинейной регрессии.
Парная нелинейная регрессия применяется для описания нелинейных видов зависимостей результирующего фактора (у) от одного независимого фактора (.х). В общем случае такие регрессии принято делить на две группы:
1) регрессии, нелинейные относительно включенных в анализ объясняющих переменных, но линейные но оцениваемым параметрам;
2) регрессии, нелинейные по оцениваемым параметрам.
К первой группе относятся следующие функции:
• полиномы разных степеней у = а + Ьхх + Ь^х2 + 63х3+ ...
• равносторонняя гипербола у = а + Ь/х.
Ко второй группе относятся следующие функции:
• степенная у = ахР
• показательная у = аЪх
• экспоненциальная у = еа+Ьх.
Функции первой группы достаточно просто сводятся к линейным, например заменой переменных. Их параметры находятся методом наименьших квадратов Функции второй группы принято делить на две подгруппы:
• внутренне линейные, которые могут быть приведены к линейному виду путем математических преобразований;
• внутренне нелинейные, которые не могут быть сведены к линейному виду.
7. Оценивание и анализ множественной линейной регрессии.
Множественная линейная регрессия - выраженная в виде прямой зависимость среднего значения величины Y от двух или более других величин X1, X2, ..., Xm. Величину Y принято называть зависимой или результирующей переменной, а величины X1, X2, ..., Xm - независимыми или объясняющими переменными.
В случае множественной линейной регрессии зависимость результирующей переменной одновременно от нескольких объясняющих переменных описывает уравнение или модель
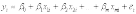,где
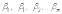- коэффициенты функции линейной регрессии генеральной совокупности,
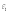- случайная ошибка.Функция множественной линейной регрессии для выборки имеет следующий вид:
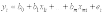,где
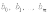- коэффициенты модели регрессии выборки,
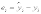- ошибка.8. Оценивание и анализ множественной нелинейной регрессии.
Если между экономическими явлениями существуют нелинейные соотношения, то они выражаются с помощью соответствующих нелинейных функций. Различают два класса нелинейных регрессий: