ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 03.02.2024
Просмотров: 23
Скачиваний: 0
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
- регрессии, нелинейные относительно включенных в анализ объясняющих переменных, но линейные по оцениваемым параметрам;
- регрессии, нелинейные по оцениваемым параметрам.
Примером нелинейной регрессии по включаемым в нее объясняющим переменным могут служить следующие функции:
- полиномы разных степеней -
, 
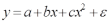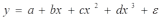, … (анализ издержек от объема выпуска);- равносторонняя гипербола -
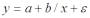(зависимость между объемом выпуска и средними фиксированными издержками, между доходом и спросом на блага, между уровнем безработицы и процентным изменением заработной платы).К нелинейным регрессиям по оцениваемым параметрам относятся функции:
- степенная -
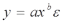(зависимость между расходами и прибылью);- показательная -
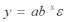(производственная функция Кобба-Дугласа);- экспоненциальная -
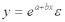(при анализе изменений переменной с постоянным темпом прироста).Нелинейные регрессии по включаемым переменным позволяют использовать МНК для оценки параметров, так как эти функции линейны по параметрам.
Рассмотрим параболу
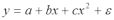. Введем замену: 
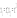. Получим: 
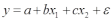- уравнение множественной линейной регрессии. Парабола 2-й степени целесообразна к применению. Если для определенного интервала значений фактора меняется характер связи признаков: прямая связь меняется на обратную или наоборот. Кривая, для которой b > 0, c < 0 используется при изучении зависимости з/п работников физического труда от возраста. При b < 0, c > 0 – зависимость затрат на производство от объема выпуска. Часто можно использовать лишь сегмент параболы.9. Применение многофакторных моделей в статистическом анализе.
Многофакторные индексные модели можно применить при проведении факторного анализа различных сторон работы АПК: при изучении эффективности использования сельскохозяйственных земель, средств производства, рабочей силы, капитальных вложений; при анализе динамики производительности труда.
Общие принципы построения многофакторных индексных моделей.
1. при построении необходимо руководствоваться экономическим содержанием показателей.
2. должна существовать возможность агрегации модели, т.е. полная модель должна распадаться на части.
3. все факторы в модели должны располагаться так, чтобы любые объединения внутри факторов внутри модели давали реальные экономические показатели.
10. Применение многофакторных моделей прогнозирования
Множественная корреляция исследует статистическую зависимость результативного признака от нескольких факторных признаков. В общем виде уравнение регрессии имеет вид:
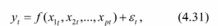
где / = 1,2,...и - количество наблюдений, р - количество параметров, st - возмущающая переменная.
Для линейной зависимости
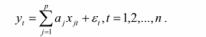
Выбор уравнения множественной регрессии включает следующие этапы:
• отбор факторов-аргументов;
• выбор уравнения связи;
• определение числа наблюдений, необходимых для получения несмещенных оценок.
Одним из важнейших требований является отбор наиболее существенных факторов. Также необходим традиционный экономический анализ, в ходе которого глубже и полнее выявляется существо, направленность и теснота связи между факторами. Последовательное введение всех конкурирующих факторов в уравнение регрессии следует осуществлять с точки зрения минимизации остаточной дисперсии.
В процессе отбора факторных признаков особое внимание следует уделять выявлению и устранению мультиколлинсарности - тесной корреляционной связи между двумя (коллинеарности) и большим числом факторных признаков.
Если в модель включаются две или несколько связанных между собой «независимых» переменных, то система нормальных уравнений не имеет однозначного решения, наряду с уравнением регрессии существуют и другие линейные соотношения.
Последствия мультиколлинеарности:
слабая обусловленность матрицы системы нормальных уравнений;
неопределенное множество коэффициентов регрессии;
сильная корреляция стандартных ошибок параметров и возрастание остаточных дисперсий;
чувствительность коэффициентов регрессии к выборке.
11. Трендовые модели прогнозирования
Трендовая модель наиболее популярна в прогнозировании. Она основана на том, что объем и особенно структура спроса характеризуются определенной степенью инерционности, т.е. потребление с запаздыванием приспосабливается к изменившимся условиям. Инерционность означает в данном случае невозможность произвольно в короткое время существенно изменить не только структуру, но и привычки потребления населения. Трендовая модель прогнозирования - это уравнение, формализующее закономерности развития спроса в базисном периоде. Модель применяется в том случае, если установлено, что найденные закономерности будут действовать на определенном отрезке времени в будущем.
В этом случае ряд динамики рассматривается как функция времени и с известным приближением описывается различными математическими уравнениями.
Из трендовых моделей в прогнозировании спроса наиболее широко используются следующие виды:
а) уравнение прямой
y = a + bx, (2.2)
б) логарифмическая функция
y = a + blgx, (2.3)
в) экспоненциальная функция
y = ax, (2.4)
г) параболическая функция
y = a + bx + cx (2.5)
д) логистическая функция
Прогноз спроса на базе трендовых моделей основывается на допущении, что все факторы, действовавшие в базисном периоде, и взаимосвязь этих факторов останутся неизменными и в прогнозном периоде. Однако такое условие в жизни часто нарушается. Поэтому метод трендовых моделей в прогнозировании спроса можно применять с упреждением на один, максимум на два интервала динамического ряда с детальным учетом всех факторов, влияющих на формирование покупательского спроса.
В таком явлении, как спрос, когда наблюдается одновременное влияние многих разнородных факторов, тесно взаимодействующих друг с другом, довольно трудно создать точную модель с хорошо интерпретирующими функциональными связями.
12. Прогнозирование на основе методов усреднения
В данном подходе прогнозирования, все будущие значения принимаются равными средним значениям исторических данных. Этот подход может быть использован для любых исторических данных.
Метод усреднения позволяет разработать прогноз, основываясь на среднем значении прошлых наблюдений.
13. Прогнозирование на основе методов сглаживания динамических рядов
Одной из задач анализа рядов динамики, является установление закономерностей изменения уровней изучаемого показателя во времени.
В некоторых случаях эта закономерность развития объекта вполне ясно отображается уровнями динамического ряда. Однако часто приходится встречаться с такими рядами динамики, когда уровни ряда претерпевают самые различные изменения. В подобных случаях для определения основной тенденции развития, достаточно устойчивой на протяжении данного периода, используют особые приёмы обработки рядов динамики.
Уровни ряда динамики формируются под совокупным влиянием множества длительных и кратковременных факторов, в том числе различных, случайных обстоятельств. В то же время выявление основной тенденции изменения уровня ряда предполагает её количественное выражение, которое свободно от случайных воздействий. Существуют различные методы выявления тенденции развития динамики. Одним из приёмов выявления основной тенденции является метод укрупнения интервалов. Этот способ основан на укрупнении периодов времени, к которым относятся уровни ряда. Например, ряд ежесуточного выпуска продукции заменяется рядом месячного выпуска продукции и т.д.
14. Прогнозирование периодических колебаний
Во многих временных рядах проявляется сезонный фактор в виде периодических регулярных колебаний, причем период таких колебаний не превышает года и равен кварталу, месяцу или неделе. Пусть выбрана аддитивная модель ряда. Представляется, что невозможно установить полностью объективное правило, разделяющее тренд и сезонность. Однако те или иные методы позволяют приближенно оценить сезонные колебания.
Простейший путь оценки сезонности для ряда y1, y2, ..., yt, ..., yn с периодом сезонности l (l=12 для ежемесячных данных, l =4 для ежеквартальных данных) заключается в вычислении разности (отношения) между средним по всем одноименным месяцам (кварталам) и средним по всем данным. В результате получаем сезонную компоненту неизменную во времени. Если временной ряд содержит выраженную тенденцию развития, то перед выделением сезонных колебаний сначала должен быть выделен тренд. Обозначим число целых периодов h=n/l, тогда:
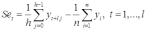.Если в последней формуле вычитание заменяется отношением, то получим так называемый индекс сезонности.
Альтернативный метод оценивания сезонной волны состоит в выделении тренда скользящими средними, например, по формуле (m=l/2):
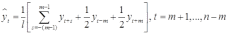,и использовании отклонений от сглаженных значений в качестве оценок сезонности:
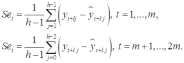(9.30)Если выбирается мультипликативная модель ряда, то в последней формуле вместо разностей берется отношение.
Разные пределы суммирования объясняются тем, что при использовании скользящей средней с четным значением длины интервала сглаживания m первых и m последних уровней будут потеряны.
Затем полученные значения сезонной компоненты корректируются так, чтобы суммарное воздействие сезонности на динамику было нейтральным. В случае аддитивной модели сумма значений сезонной составляющей для одного периода должна быть равна нулю. Поэтому окончательные оценки сезонности получаются по формуле:
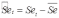, t=1,…,l, (9.31)где
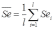
. В случае мультипликативной модели:
, 
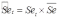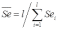.15. Прогнозирование спроса и предложения
Прогнозы спроса и предложения составляют, используя методы планирования человеческих ресурсов и техники моделирования. В крупных организациях использование моделирования приносит особенно хорошие плоды, поскольку позволяет провести анализ чувствительности воздействия различных предположений относительно будущего (т. е. ответить на вопросы типа «А что, если?..»).
Там, где существуют обширные базы данных относительно потока, требования к атрибутам (спецификации сотрудников) и оценки показателей труда и потенциала, можно пользоваться экспертными системами. Подобные системы позволяют установить отношения между возможностями и свойствами личности, которые необходимы для использования этих возможностей, поэтому консультанты по вопросам карьеры могут взять набор личностных характеристик и определить, какие возможности больше всего подходят для данного конкретного человека. На стадии планирования карьеры они могут также выявить людей с нужными способностями и навыками для конкретных рабочих мест и предоставить информацию относительно программ управления карьерой, которые обеспечат соответствие атрибутов и рабочих мест и развитие карьеры с надлежащей скоростью. Для этой цели были специально разработаны такие системы управления карьерой, как ExecuGROW (Control Data).
Однако и у сложности есть предел. Существует так много переменных и непредсказуемых изменений факторов, как спроса, так и предложения, что можно проводить лишь ежегодную проверку, чтобы увидеть, какая взаимосвязь существует между числом менеджеров, которые определенно уйдут на пенсию в течение ближайших четырех-пяти лет, и количеством менеджеров, стоящих на ступеньку ниже, которые станут их преемниками. Если сравнение этих данных выявит серьезный дисбаланс, то необходимо предпринять шаги, направленные на уменьшение или устранение дефицита, или рассмотреть другие возможности использования тех, кто вряд ли пойдет на повышение.
16. Прогнозирование и анализ экономического роста на основе модели производственной функции Кобба-Дугласа
Одной из важнейших проблем при анализе экономического роста является определение вклада каждого производственного вклада в увеличение выпуска продукции. Решение этой проблемы важно для определения оптимального сочетания факторов производства, обеспечивающего увеличение темпов экономического роста.