В качестве инструмента факторного анализа обеспечения экономического роста в большинстве современных моделей используется производственная функция, отражающая связь не только между величиной выпуска и затратами факторов производства, но и уровнем технологического развития.

Впервые такая модель была предложена в 20-х гг. XX века американским экономистом П.Дугласом и математиком Х.Коббом.

Производственная функция Кобба-Дугласа является частным случаем производственной функции (1) и имеет следующий вид:

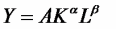 , (6)

где:

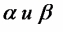 – коэффициенты эластичности объема выпуска по затратам, капитала (K) и труда (L) соответственно;

 .

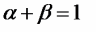Параметры 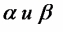  были определены авторами в результате эмпирического исследования обрабатывающей промышленности в США и составляют 0,25 и 0,75 соответственно.

Это означает, что повышение затрат капитала (K) на 1% вызовет рост выпуска продукции (Y) на 0,25%, а повышение затрат труда (L) на 1% вызовет рост выпуска продукции на 0,75%. Таким образом, вклад труда в ВВП в три раза больше вклада физического капитала.

Модель Кобба-Дугласа позволяет подойти к измерению вклада технологического прогресса (A) в экономический рост. Если уравнение (6) переписать в темпах прироста выпуска, то получим следующую формулу:

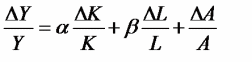 , (7)

где:

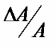 – показывает вклад прироста совокупной производительности факторов K и L, т.е. вклад технологического прогресса.

17. Подбор стационарной модели ARIMA для ряда наблюдений

Структура модели ARIMA описывается тремя параметрами (р, q, k). Кроме того, разные по форме модели могут быть довольно близки друг другу. Поэтому весьма важно по возможности правильно определить структуру модели. Рассмотрим этапы идентификации.

1. Подбирается порядок модели k. Для этого используется либо метод последовательных разностей, либо анализ автокорреляционных функций процессов Dy(t), D²y(t), … - пока не достигнем быстрого затухания (стационарности) автокорреляционной функции для некоторого k. Дж.Бокс и Г.Дженкинс предлагают взять за визуальный критерий стационарности быстрое убывание значений выборочной АКФ. Использование завышенного порядка разности приводит к росту дисперсии ошибок и к заметному росту дисперсии прогноза.

---

2. Находим y_k(t)=D^ky(t) и идентифицируем ARMA(р, q) модель.

18. Нестационарные ARIMA модели

В случае, когда временной ряд не является стационарным, необходимо оценить и исключить из временного ряда нестационарные особенности, прежде чем минимизировать ожидаемые потери в задаче (1). Таким образом, прогноз xˆT +1 нестационарного временного ряда будет складываться из двух частей: прогноз нестационарной компоненты xˆ ns T +1 и прогноз стационарной компоненты xˆ s T +1:

xˆT +1 = ˆx ns T +1 + ˆx s T +1.

Алгоритм прогнозирования нестационарной компоненты временного ряда должен быть таким, чтобы регрессионные остатки при прогнозе доступной для обучения истории x r = {(ri) T i=1 | ri = xi − xˆ ns i } были стационарным временным рядом, значения которого сгенерированы из одного распределения с плотностью γ(u).

В качестве алгоритма прогнозирования нестационарной части ряда предлагается использовать ARIMA. Для оптимизации параметров этот алгоритм использует квадратичную функцию потерь Lsq(ˆx, x) = (ˆx − x) 2 , по которой строится функционал потерь:

Q(f ns , x) = 1 T X T i=1 Lsq(f ns(w, xi , 1), xi+1); xi = {x1 · · · xi}.

19. Прогнозирование с учетом сезонной составляющей в ППП Excel.

Для прогнозирования объема продаж, имеющего сезонный характер, предлагается следующий алгоритм построения прогнозной модели:

1.Определяется тренд, наилучшим образом аппроксимирующий фактические данные. Существенным моментом при этом является предложение использовать полиномиальный тренд, что позволяет сократить ошибку прогнозной модели.

2.Вычитая из фактических значений объёмов продаж значения тренда, определяют величины сезонной компоненты и корректируют таким образом, чтобы их сумма была равна нулю.

3.Рассчитываются ошибки модели как разности между фактическими значениями и значениями модели.

4.Строится модель прогнозирования:

F = T + S ± E

где: 
F– прогнозируемое значение; 
Т– тренд; 
S – сезонная компонента; 
Е - ошибка модели.

5.На основе модели строится окончательный прогноз объёма продаж. Для этого предлагается использовать методы экспоненциального сглаживания, что позволяет учесть возможное будущее изменение экономических тенденций, на основе которых построена трендовая модель. Сущность данной поправки заключается в том, что она нивелирует недостаток адаптивных моделей, а именно, позволяет быстро учесть наметившиеся новые экономические тенденции.

---

F_{пр t} = a F_{ф t-1} + (1-а) F_{м t}

где: 
F_{пр t} - прогнозное значение объёма продаж; 
F_{ф t-}1 – фактическое значение объёма продаж в предыдущем году; 
F_{м t}- значение модели; 
а –константа сглаживания

Практическая реализация данного метода выявила следующие его особенности:

• 
  для составления прогноза необходимо точно знать величину сезона. Исследования показывают, что множество продуктов имеют сезонный характер, величина сезона при этом может быть различной и колебаться от одной недели до десяти лет и более;
  
• 
  применение полиномиального тренда вместо линейного позволяет значительно сократить ошибку модели;
  
• 
  при наличии достаточного количества данных метод даёт хорошую аппроксимацию и может быть эффективно использован при прогнозировании объема продаж в инвестиционном проектировании.
  

20. Адаптивные методы прогнозирования ППП Statistica.

Адаптивные методы используются в условиях сильной колеблемости уровней динамического ряда и позволяют при изучении тенденции учитывать степень влияния предыдущих уровней на последующие значения динамического ряда.

К адаптивным методам относят:

- методы скользящих и экспоненциальных средних,

- метод гармонических весов,

- методы авторегрессионных преобразований.

Адаптивный метод относится к краткосрочному прогнозированию.

Методы прогнозирования - экстраполяция тренда, регрессионно - корреляционный метод не всегда применимы. Тренд, регрессия описывают экономические процессы в среднем. Существуют такие нестационарные экономические процессы, математическое ожидание изменяется или экономический процесс описывается короткими динамическими рядами. Для увеличения надежности прогноза экономического развития в быстроизменяющихся условиях неполной информации возможно применение адаптивных моделей. Эти модели отражают текущие свойства динамического ряда и способны непрерывно учитывать эволюцию динамических характеристик, изучаемых процессов. Эти методы базируются на самокорреляционных моделях, которые учитывают результаты прогнозов, сделанных на предыдущем шаге. Модель постоянно впитывает новую информацию, приспосабливается к ней, поэтому отражает тенденцию развития, существующую в данный момент. Именно поэтому адаптивные модели особенно удачно используются при краткосрочном прогнозировании.

---

Адаптивные методы позволяют учесть различную информационную ценность уровней временного ряда, а также степень устаревания данных.

Начало адаптивному направлению в прогнозировании положила модель экспоненциального сглаживания. Например: Дан динамический ряд показателей хt.Модель можно записать следующим образом:

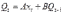 (5.13)

A, B – параметры модели, A оценивает информацию настоящего, B – прошлого.

0–A<1; А+В=1

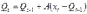 . (5.14)

Новый прогноз получается в результате корректировки предыдущего на 1 шаг. Для увеличения веса свежих наблюдений необходимо увеличить параметр адаптации А. Для сглаживания случайных отклонений уровней заданного динамического ряда параметр А необходимо снижать. Если эти 2 требования противоречат друг к другу, значит модель нуждается в оптимизации. Достигается это подбором параметра адаптации А:

А=0,3 – принимают во всех случаях, но это оспаривается, для каждой модели параметр должен быть свой.

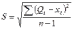 (5.15)

Каждый параметр адаптации А дает свою стандартную ошибку S. График с увеличением А увеличится и ст. от А.

21. Модели стационарных и нестационарных временных рядов ППП Statistica.

Стационарные временные ряды.

Важное значение в анализе временных рядов имеют стационарные временные ряды, вероятностные свойства которых не изменяются во времени. Временной ряд y_t (t=1, 2, …, n) называется строго стационарным, если совместное распределение вероятностей n наблюдений y₁, y₂,…, y_n такое же, как и n наблюдений y_1+τ, y_2+τ,…, y_n+τ при любых n, t, и τ. Таким образом, свойства строго стационарных рядов не зависят от момента времени t.

Нестационарные временные ряды.

Пусть имеется временной ряд

y_t = ρy_t-1+ ξ_t.

Предположим, что ошибки ξ_t независимы и одинаково распределены, т.е. образуют белый шум. Перейдем к разностным величинам:

Δy_t = λy_t-1+ ξ_t,

где Δy_t = y_t – y_t-1, λ= ρ-1.

Если ряд Δy_tявляется стационарным, то исходный нестационарный ряд y_tназывается интегрируемым (или однородным).

Нестационарный ряд 

---

y_tназывается интегрируемым (однородным) k-го порядка, если после k-кратного перехода к приращениям

d^ky_t = d^k-1y_t – d^k-1y_t-1,

где d¹y_t = Δy_t, получается стационарный ряд d^ky_t.

Если при этом стационарный ряд d^ky_t корректно идентифицируется как АРСС(p,q), то нестационарный ряд y_t обозначается как АРПСС(p,k,q). Это означает модель авторегрессии – проинтегрированной скользящей средней (другое обозначение - ARIMA(p,k,q)) порядков p, k, q, которая известна как модель Бокса-Дженкинса. Процедура подбора такой модели реализована во многих эконометрических пакетах.

22. Построение уравнения множественной регрессии в ППП Excel и ППП Statistica.

1. Встроенная статистическая функция ЛИНЕЙН определяет параметры линейной регрессии y=a+bx. Порядок вычисления следующий:

1) введите исходные данные:

	А	В	С
	Территория региона	Прожиточный минимум, х	Среднемесячная зарплата, у

2) выделите область пустых ячеек 5´2 (5 строк, 2 столбца) для вывода результатов регрессионной статистики или область 1´2 – для получения только оценок коэффициентов регрессии;

---

Смотрите также файлы

• План решения педагогической задачи 1.docx

• 1 задание Перечислите положительные и отрицательные стереотипы, используемые в рекламе. В каких случаях будет наиболее эффективным применение положительных стереотипов, а в каких отрицательных.docx

• Лабораторная работа 1 по дисциплине (учебному курсу) Криминалистика Студент Никитина Дарья Романовна.docx

• Группа Студент москва 2022г. Вопросы и задания.docx

• Медицинское страхование и его виды.rtf