Среднее квадратическое отклонение динамической нагрузки колеса на рельс, S_р, кг, от вертикальных колебаний надрессорного строения определяется по формуле
S_р = 0,08
Среднее квадратическое отклонение динамической на­грузки колеса на рельс, S_нп, кг, от сил инерции необрессоренных масс 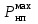, возникающих при проходе изолированной неровности пути определяется по формуле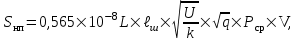

где	L	–	коэффициент, учитывающий влияние колеб. масс подвижного состава и пути, типа рельса, материала шпал, рода балласта на образование динамических неровностей пути;
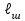		–	расстояние между осями шпал, см;
	U	–	модуль упругости подрельсового основания, кг/см2;
	k	–	коэффициент относительной жесткости рельсового основания и рельса, см-1;
	q	–	отнесенный к колесу вес необрессоренных частей, кгс;
	V	–	скорость движения, км/ч.

Среднее квадратическое отклонение динамической нагрузки колеса на рельс ,S_ннк, кг, от сил инерции необрессоренной массы 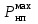при движении колеса с плавной непрерывной неровностью на поверхности катания определяется по формуле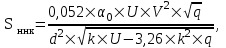

где		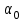–	коэффициент, учитывающий отношение необрессоренной части подвижного состава и участвующий во взаимодействии массы пути;
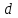		–	диаметр колеса, см.

---

Среднее квадратическое отклонение динамической нагрузки колеса на рельс, S_инк, кг, от сил инерции необрессоренной массы Ринк, возникающих из-за наличия на поверхности катания плавных изолированных неровностей определяется по формуле

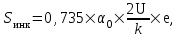
где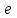

–

наибольшая расчетная глубина неровности колеса, см.

Посчитаем значение среднего квадратического отклонения динамической вертикальной нагрузки колеса на рельс, S, кг, и динамическую максимальную нагрузку, 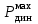, кг, от колеса на рельс для локомотива ВЛ-10 при движении по прямой в летний период и для вагона при движении по кривой (R=600) в летний период.

Локомотив ВЛ-10 при движении по прямой в летний период:


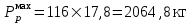
= 0,75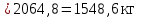



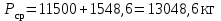
S_р = 0,08










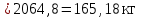
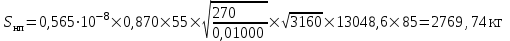
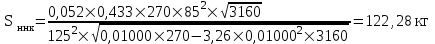
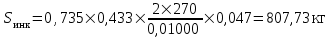
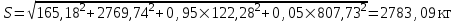
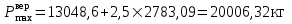
Вагон при движении по кривой (R=600) в летний период:



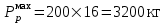
= 0,75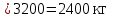



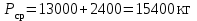
S_р = 0,08

---

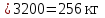
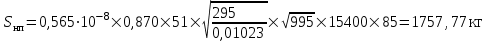
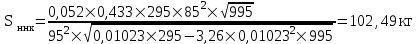
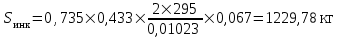
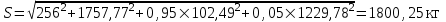
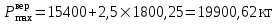
Остальные значения сведем в Таблицу 3.

Таблица 3. Определение среднего и максимального вероятного значения динамической силы воздействия от колеса на рельс.

Элемент пути		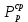		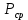		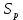		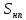		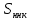		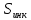			S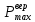
Локомотив	Прямая	1548,6		13048,6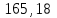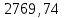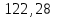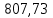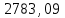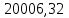
	Кривая R=600м	1548,6		13048,6		165,18		2654,22		123,97		862,68		2669,08		19721,3
Вагон 8-осный	Прямая	2400		15400		256		1834,27		99,6		1151,45		1872,38		20080,95
	Кривая R=600м		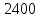		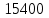	256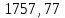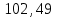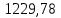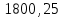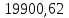

---

---

1.3. Определение напряжений в элементах верхнего строения пути
При расчете рельса как балки на сплошном упругом основании система сосредоточенных колесных нагрузок заменяется эквивалентными одиночными нагрузками, соответственно при определении изгибающих моментов и напряжений в рельсах с помощью функции 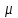и при определении нагрузок и прогибов с помощью функции .

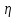Максимальная эквивалентная нагрузка, 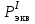, кг, для расчетов напря­жений в рельсах от изгиба и кручения определяется по формуле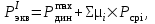

где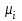

–

ординаты линии влияния изгибающих моментов рельса в сечениях пути, расположенных под колесными нагрузками от осей экипажа, смежных с расчетной осью.

Максимальная эквивалентная нагрузка, 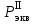, кг, для расчетов напряжений и сил в элементах подрельсового основания определяется по формуле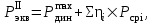

где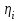

–

ординаты линии влияния прогибов рельса в сечениях пути, расположенных под колесными нагрузками от осей экипажа, смежных с расчетной осью.

Напряжения изгиба и кручения в кромках подошвы рельса, σ_кп, кгс/см², определяется по формуле

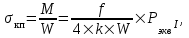
где		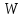–	момент сопротивления рельса относительно наибольшего удаленного волокна от подошвы, см3;
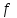		–	коэффициент перехода от осевых напряжений к рамочным.

---

Смотрите также файлы

• Кнтізбелік таырыпты жоспар Пні Физика Сыныбы 7.docx

• Методические рекомендации для студентов по учебной практике пм. 06. 01 основы вожатской деятельности.docx

• Содержание хозяйственной операции.docx

• Развитие геодезии в России.docx

• Отчет по лабораторной работе 1 Метод потенциалов собственной поляризации.docx