Мазмұны

Кіріспе......................................................................................................................2

Алгебралық теңдеулердің теориялық ерекшеліктері.

§1. Бір белгісізі бар теңдеулер. Теңдеудің түбірі...................................................4

§2. Сызықтық теңдеулер.........................................................................................7

§3. Квадрат теңдеулер. Виет теоремасы...............................................................9

§4. Сызықтық және квадраттық теңдеулер..........................................................13

§5. Үшінші дәрежелі теңдеулер............................................................................16

§6. Төртінші дәрежелі теңдеулер..........................................................................20

§7. Құрамында параметрі бар квадраттық теңдеулер ........................................22

Қорытынды..........................................................................................................27

Әдебиеттер тізімі..................................................................................................28

Кіріспе

Қазіргі әлемдегі математиканың рөлі зор. Ол адамзат қоғамының күрделі және қарқынды даму процесінде құрметті орын алады және өзі өнімді күшке айналады. Біздің күндеріміздің тәжірибесі математикалық есептердің жаңа түрлерінің ең бай көзі болып табылады. Бұл есептердің барлығы физикалық, инженерлік және технологиялық мәселелерді алға тартып қана қоймай, сонымен қатар компьютерлерге арналған бағдарламалау, тармақталған кездейсоқ процестер, оңтайлы теңдеу теориясы және т.б. сияқты математиканың жаңа бөлімдерін құруға әкелді.

Бүгінгі таңда "алгебралық теңдеулер" ұғымы жалпы математикалық мәдениеттің қажетті элементіне айналды. Сонымен қатар, студенттер осы материалдың негізгі анықтамаларын біліп қана қоймай, Алгебралық теңдеулерді, олардың шешімдерін терең зерттеу қажеттілігін түсінуі керек. Теңдеулерді зерттеу оқушылардың ой-өрісін кеңейтуге, олардың білім сапасын жақсартуға және жоғары оқу орындарына түсуге көмектеседі. Сондықтан зерттеудің өзектілігі Алгебралық теңдеулерді зерттеу және шешу болып табылады.

Бұл мәселені ғылыми-әдістемелік әдебиеттерде қарастыру мектептегі математика курсында осы материалды зерттеу мәселелерін шешпейді. Біріншіден, зерттелетін ұғымдарды тереңірек зерттеуге жеткілікті уақыт бөлінбейді; екіншіден, бағдарламада математикалық ойлауды дамытуға, ғылыми дүниетанымды қалыптастыруға ықпал ететін негізгі жалпы білім беретін мектепте теңдеулерді, олардың шешімдерін жеткілікті егжей-тегжейлі талдау қарастырылмаған.

Қоғам дамуының қазіргі кезеңінде математикаға технологияландыру мен ақпараттандырумен елеулі талаптар қойылады.

---

Сондықтан, біздің зерттеуіміздің проблемасын біз оқушылардың осы материал туралы білімдерін жүйелеу және тереңдету қажеттілігінен және негізгі мектепте осы материалды оқуда жүйеліліктің болмауынан көреміз, бұл оқу процесін оңтайлы етуге мүмкіндік бермейді.

Зерттеу нысаны: негізгі жалпы білім беретін мектепте математиканы оқыту процесі.

Зерттеу пәні: алгебралық теңдеулер және оларды Математиканы оқыту курсының құрамдас бөлігі ретінде шешу жолдары.

Зерттеудің мақсаты: теория мен практикада бір белгісіз Алгебралық теңдеулерді шешу жолдарын зерттеу, алгебралық теңдеулердің әртүрлі түрлерін шешу бойынша оқушылардың білімін, дағдылары мен дағдыларын арттыруға ықпал ететін әдістемелік жағдайларды анықтау және оларды іс жүзінде сынау.

Зерттеудің мақсаттарына сүйене отырып, келесі міндеттер туындайды:

1. Бір белгісіз Алгебралық теңдеулерді шешудің әртүрлі түрлері мен тәсілдерін анықтаңыз.

2. Алгебралық теңдеулерді шешуде білімнің, дағдылардың және дағдылардың сапалы қалыптасуына ықпал ететін әдіснамалық жағдайларды анықтаңыз.

3. Алгебралық теңдеулерді шешудің әртүрлі тәсілдерін негізгі мектепте тәжірибеде сынап көріңіз.

Гипотеза: негізгі жалпы білім беретін мектеп курсында алгебралық теңдеулер бойынша оқу материалын жүйелі түрде ұсыну математика бойынша білімді тереңдетуге және оңтайландыруға және жоғары математика курсын меңгеру үшін берік негіз құруға ықпал етеді.

Біздің зерттеуіміздің әдіснамалық негізі оқушылардың қажеттіліктерін бүкіл педагогикалық жүйенің орталығына қоюға мүмкіндік беретін гуманистік тұлғаға бағытталған оқыту тұжырымдамасы болды.

Теориялық маңыздылығы: ғылыми-әдістемелік дереккөздерді теориялық жалпылау негізінде бір белгісіз Алгебралық теңдеулерді шешудің ең оңтайлы әдісі анықталды.

Зерттеу әдістері: зерттеу мәселесі бойынша ғылыми-әдістемелік әдебиеттерді талдау, эмпирикалық зерттеу әдістері: бақылау, сауалнама, бақылау тапсырмалары, нәтижелерді статистикалық өңдеудің эксперименттік әдістері.

Алгебралық теңдеулердің теориялық ерекшеліктері.

§1. Бір белгісіз теңдеулер. Теңдеудің түбірі.

Екі өрнектің теңдігіне кіретін әріптік шамалар 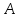және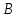

---

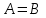: , шарт бойынша есептер тең емес болуы мүмкін. Олардың кейбіреулері белгілі немесе параметрлер болып саналады. Олар өздерінің барлық рұқсат етілген мәндерін қабылдай алады. Басқа әріптік шамалар белгісіз.

Әріптермен көрсетілген белгісіз сандарды қамтитын теңдік теңдеу деп аталады.

Теңдеуге кіретін белгісіздер санына байланысты олар бір, екі және т. б. белгісіз теңдеулерді қарастырады.

Теңдеулердегі белгісіз шамалар әдетте әріптермен 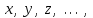ал белгілі (немесе Параметрлер) – 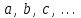әріптермен белгіленеді

Алдымен бір белгісіз теңдеуді қарастырайық



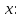
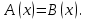
Теңдік белгісінің сол және оң жағындағы өрнектер теңдеудің сол және оң жақтары деп аталады. Теңдеу бөлігінің әрбір термині теңдеу термині деп аталады.

Рұқсат етілген мәндер аймағы (қысқаша ОДЗ) немесе 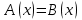теңдеуді анықтау аймағы белгісіз барлық сандық мәндердің жиынтығы деп аталады, олардың әрқайсысында өрнек мағынасы бар 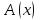және 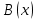бір уақытта.

Анықтама. Теңдеудің түбірі (немесе шешімі) белгісіз мән деп аталады, онда бұл теңдеу дұрыс теңдікке айналады.

Әлбетте, теңдеудің түбірі осы теңдеудің ОДЗ-ге жатады.

Теңдеуді шешу дегеніміз-оның барлық тамырларын табу немесе олардың жоқтығын анықтау.

Мысалы, 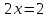теңдеудің бір түбірі бар 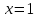; 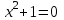теңдеудің R жиынында түбірі жоқ: кез келген нақты сан 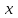үшін әрқашан .

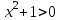Анықтама. Екі теңдеу эквивалентті (эквивалентті) деп аталады, егер бір теңдеудің кез-келген түбірі екіншісінің түбірі болса және керісінше. Егер екі теңдеудің де түбірлері (шешімдері) болмаса, онда олар эквивалентті болып саналады.

Басқаша айтқанда, эквиваленттер дегеніміз-түбірлерінің жиынтығы сәйкес келетін теңдеулер.

---

Егер теңдеулер және 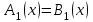эквивалентті болса, онда олар жазады .

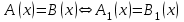Мысалы, 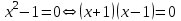; 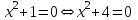, өйткені бұл теңдеулердің нақты түбірі жоқ. Теңдеулер 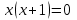және 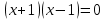тең емес екені анық.

Әр түрлі түрлендірулер арқылы теңдеуді шешкен кезде оны қарапайым, оған тең теңдеумен ауыстыруға тырысыңыз. Алайда, мұндай ауыстыру әрдайым сәтті бола бермейді. Содан кейін келесі екі жағдай болуы мүмкін:

1. Жаңа теңдеуге көшу кезінд түбірлердің жоғалуы мүмкін. Мысалы, 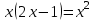теңдеуден аббревиатурамен теңдеуге ауысқан кезде 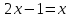түбірдің жоғалуы орын алады . Сондықтан жаңа теңдеуге көшу кезінде берілген теңдеудің түбірін жоғалту мүмкіндігін ескеру қажет.

2. Жаңа теңдеуде түбір емес тамырлар болуы мүмкін берілген теңдеу (бөгде түберлер деп аталады). Мысалы, 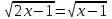теңдеуден 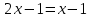теңдеуге ауысқанда, бастапқы теңдеудің екі бөлігін квадраттау арқылы біз осы теңдеудің 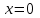бөгде түбірін аламыз. Сондықтан олар көбінесе тамырларды осы теңдеуге ауыстыру арқылы тексереді.

Естеріңізге сала кетейік, сандық теңдіктер келесі қасиеттерге ие:

1) егер оның екі бөлігіне де қосылса, сандық теңдік бұзылмайды

бірдей сан;

2) егер оның екі бөлігі де көбейтсе немесе көбейтілсе, сандық теңдік бұзылмайды, нөлден басқа бірдей санға бөліңіз.

Сандық теңдеулер мен эквивалентті теңдеулер ұғымдарының қасиеттерінен теңдеулердің келесі негізгі қасиеттері шығады:

1) Теңдеу , (1) 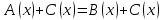, (2) теңдеуге тең , мұндағы 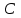- теңдеудің рұқсат етілген мәндерінің жиынында мағынасы бар сан немесе кейбір өрнек

---

.

Дәлелдеуі:

Біз теңдеудің 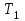шешімдері арқылы (1), ал теңдеудің көптеген 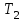шешімдері арқылы (2) белгілейміз. Сонда (1) және (2) теңдеулер тең болады 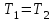. Бірақ бұған көз жеткізу үшін кез-келген түбір (2) теңдеудің түбірі 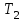және керісінше, кез-келген түбір (1) теңдеудің түбірі 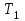екенін көрсету керек.

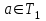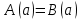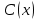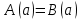Теңдеудің түбірі а-санына тең болсын (1). Содан кейін (1) теңдеуіне ауыстырған кезде оны нақты сандық теңдікке айналдырады , ал өрнек сандық өрнекке айналады . Шынайы теңдіктің екі бөлігіне де сандық өрнек қосайық . Біз шынайы сандық теңдіктердің қасиеттеріне сәйкес шынайы 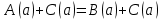сандық теңдікті аламыз .

Бірақ бұл теңдіктегі а-саны (2) теңдеуінің түбірі екенін көрсетеді.

Сонымен, (1) теңдеудің әрбір түбірі (2) теңдеуінің түбірі, яғни .

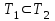Енді теңдеудің түбірі b-саны болсын (2). Олай болса теңдеуді 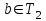ауыстырған кезде оны шынайы сандық теңдікке айналдырады .

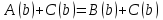Осы теңдіктің екі бөлігіне де 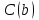сандық өрнек қосайық . Біз санның b-саны (1) теңдеуінің түбірі екенін көрсететін нақты сандық теңдеуді 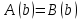аламыз.

Сонымен, (2) теңдеудің әрбір түбірі (1) теңдеуінің түбірі, яғни .

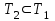Сонымен, 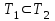және 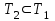тең жиындардың анықтамасы бойынша, яғни (1) және (2) теңдеулер

---

Смотрите также файлы

• Тема Прочитайте и переведите текст. Обратите внимание на выделенные слова и словосочетания это основные лексические единицы данной темы..doc

• азастан тарихы пнінен 7 сыныпты кнтізбеліктаырыпты жоспар жылына 72 с, аптасына 2 c.docx

• 1 Тапсырма Сратара жауап бер.docx

• Закон единства количественных и качественных изменений. Диалектика связи эволюции и революции в развитии.docx

• Методические рекомендации по написанию, оформлению и защите.pdf