ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 04.02.2024
Просмотров: 31
Скачиваний: 0
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
теңдеудегі 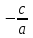 шаманы сол жаққа ауыстырсақ,
шаманы сол жаққа ауыстырсақ, 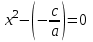 аламыз .
аламыз .
Сонымен , содан кейін
, содан кейін 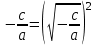 . Сондықтан
. Сондықтан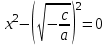 .
.
Осы теңдеудің сол жағын көбейту арқылы біз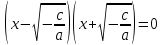 аламыз .
аламыз .
Егер коэффициенттердің кем дегенде біреуі нөлге тең болса, бұл теңдік нөлге тең болады.
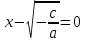 қарастырып,
қарастырып,  аламыз ;
аламыз ; 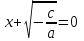 қарастырып,
қарастырып,  табамыз.
табамыз.
Демек ,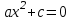 теңдеудің
теңдеудің  кезінде екі түбірі бар: ол
кезінде екі түбірі бар: ол  ,
,  . Жауап көбінесе
. Жауап көбінесе 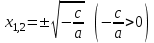 түрінде жазылады .
түрінде жазылады .
Мысалы,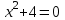 толық емес квадрат теңдеудің нақты түбірі жоқ. Толық емес
толық емес квадрат теңдеудің нақты түбірі жоқ. Толық емес 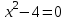 квадрат теңдеу үшін біз
квадрат теңдеу үшін біз 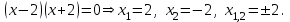 аламыз.
аламыз.
Бұл теңдікті басқалай шешуге болады:
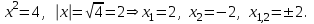
3.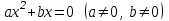 теңдеуді оның сол жағын көбейткіштерге бөлу арқылы шешуге болады. Әлбетте
теңдеуді оның сол жағын көбейткіштерге бөлу арқылы шешуге болады. Әлбетте 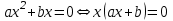 , осыдан
, осыдан  ,
, 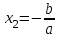 . Мысалы,
. Мысалы, 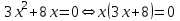 , осыдан
, осыдан ,
, 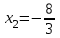 .
.
Жалпы жағдайда квадрат теңдеулерді шешу үшін толық квадратты таңдау әдісі қолданылады. [5, c.120]
Бұл әдісті қолдану алдымен мысалдармен түсіндіріледі.
Мысал 1.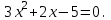 квадрат теңдеуді шешіңіз
квадрат теңдеуді шешіңіз
Шешім. Теңдеудің екі бөлігін де 3 ке бөлейік :
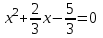
Толық квадратты таңдау әдісін қолданамыз:
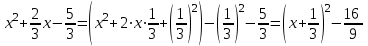 .
.
Сондықтан біз
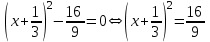 аламыз,
аламыз,
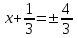 . Сондықтан,
. Сондықтан,
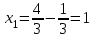 ,
, 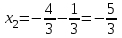 .
.
Толық квадратты бастапқы теңдеуде және алдын-ала 3 ке бөлусіз бөлуге болады (белгісіз квадраттағы коэффициент):
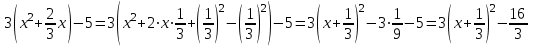 Сондықтан
Сондықтан
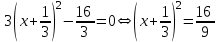 және т. б. [2, с.107]
және т. б. [2, с.107]
Енді жалпы түрдің квадрат теңдеуін қарастырайық

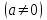 . (1)
. (1)
Толық квадратты таңдау әдісін қолданамыз. Ол үшін теңдеудің сол жағын келесі түрде жазайық:
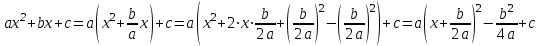
Сондықтан
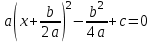 немесе
немесе 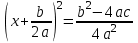 . (2)
. (2)
Қосымша шешім алынған теңдеудің оң жағындағы белгіге байланысты (2).
Өйткені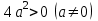 , оң жақ бөліктің белгісі
, оң жақ бөліктің белгісі 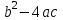 өрнек белгісімен сәйкес келеді . [15, c.163]
өрнек белгісімен сәйкес келеді . [15, c.163]
Анықтама.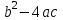 өрнек
өрнек 
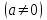 квадрат теңдеудің дискриминанты деп аталады және
квадрат теңдеудің дискриминанты деп аталады және 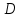 әріппен белгіленеді :
әріппен белгіленеді : 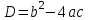 .
.
Үш жағдайды қарастырайық:.
1.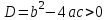 .
.
Бұл жағдайда (2) теңдеуді келесідей жазуға болады:
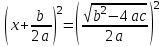 ;
;
сондықтан,
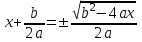
,
осыдан
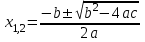 , (3)
, (3)
немесе
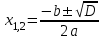 , (4)
, (4)
мұндағы - теңдеудің дискриминанты (1).
- теңдеудің дискриминанты (1).
2.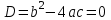 .
.
Бұл жағдайда (2) теңдеу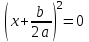 форманы алады,
форманы алады,
Қайдан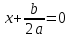 , яғни
, яғни 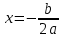 .
.
Осылайша, егер дискриминант нөлге тең болса, яғни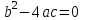 теңдеудің жалғыз түбірі
теңдеудің жалғыз түбірі 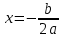 болады .
болады .
3.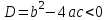 .
.
Бұл жағдайда (2) теңдеудің оң жағында теріс сан, ал сол жағында теріс емес (оң немесе нөлге тең) болады. Сондықтан , егер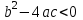 болса, онда (2) теңдеу, демек
болса, онда (2) теңдеу, демек  теңдеудің нақты түбірі жоқ.
теңдеудің нақты түбірі жоқ.
Қорытынды. квадрат теңдеудің
квадрат теңдеудің 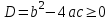 дискриминанты кезінде ғана нақты түбірі болады; егер
дискриминанты кезінде ғана нақты түбірі болады; егер 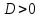 , онда түбірлер әр түрлі; егер
, онда түбірлер әр түрлі; егер 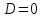 , онда түбірлер тең. Квадрат теңдеудің түбір формуласы (3) немесе (4) түрінде болады.
, онда түбірлер тең. Квадрат теңдеудің түбір формуласы (3) немесе (4) түрінде болады.
Бұл формула бойынша толық емес квадрат теңдеулердің түбірлерін табуға болады, бірақ оларды көрсетілгендей толық емес квадрат теңдеудің сол жағын көбейту арқылы есептеу оңайырақ.
§4. Сызықтық және квадраттық теңдеулер
Екі айнымалысы бар сызықтық теңдеу: Бір айнымалысы бар сызықты теңдеу ах = в түрінде болады. Екі айнымалысы бар сызықты теңдеу ах + ву = с (1 ) түрінде беріледі,мұндағы х,у - айнымалылар, а,в,с – нақты сандар және а мен в бір мезгілде нөлге тең емес.
Мысалы: 2х + 3у = 8; 0,6х – 1,2у= 3;
Екі айнымалысы бар сызықтық теңдеуде әр қосылғыштағы айнымалылардың дәреже көрсеткіштерінің қосындысы 1- ге тең болуы керек. (1) теңдеуді қанағаттандыратын кез-келген сандар жұбы екі айнымалысы бар сызықтық теңдеудің шешімі деп аталады. Мыс: х+у=12 теңдеуінің шешімдер жұбы: (1;11), (5;7),,(9;3),(3;9) т.б Бір айнымалыны екіншісі арқылы өрнектеу үшін: 2у – х = 5 теңдеуінде х айнымалысын у айнымалысы арқылы өрнектейік. x = 2у – 5. Екі айнымалысы бар сызықтық теңдеудің ең болмағанда бір айнымалысының коэффициенті нөлге тең болмаса,оның графигі түзу сызық болады.
Екі айнымалысы бар сызықтық емес теңдеулер және оның шешімі: Егер теңдеулер құрамының біреуі сызықтық емес теңдеу болса,онда екі айнымалысы бар теңдеулер жүйесі екі айнымалысы бар сызықтық емес теңдеулер жүйесі деп аталады.
Мысал:
ж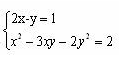 үйедегі бірінші теңдеудің графигі түзу сызық екені белгілі,ал екінші теңдеу графигін білмейміз. Мұндай жүйелерді шешудің негізгі жолы – ауыстыру тәсілі. Шешу алгоритмі:
үйедегі бірінші теңдеудің графигі түзу сызық екені белгілі,ал екінші теңдеу графигін білмейміз. Мұндай жүйелерді шешудің негізгі жолы – ауыстыру тәсілі. Шешу алгоритмі:
1)бірінші дәрежелі теңдеуден айнымалының бірін екіншісі арқылы өрнектеп жазу;
2)табылған өрнекті екінші дәрежелі теңдеудегі айнымалының орнына қойып бір айнымалысы бар теңдеу аламыз;
3)шыққан теңдеуді шешкенде айнымалылардың біреуінің мәндері табылады;
4)Осы мәндер арқылы екінші айнымалының мәні табылады.
Егер айнымалылардың біреуінің коэффициенттері қарама-қарсы сандар болса мүшелеп қосу тәсілін қолданамыз.
Сызықтық теңдеу – белгісіздері (айнымалы шамалары) 1-дәрежелі болып келетін және белгісіздердің көбейтінділері қатыспайтын теңдеу.
Мысалы:
а1х1 + а2х2 +…+ + аnхn = b (1)
түріндегі теңдеу n белгісізі (аі≤0, і=1, 2, …, n) бар сызықтық теңдеуге жатады. Егер (1) теңдеудегі аi=0 (і=2, 3, …, n) болып, бірақ а1≤0 болса, онда ол а1х = b немесе ах = b (а1 = а) түріндегі бір белгісізі бар сызықтық теңдеуге айналады. Берілген айнымалыларға қатысты бірнеше сызықтық теңдеулер жиынтығы Сызықтық теңдеулер жүйесін құрады:
a11x1 + a12x2 +…+ a1nxn = b1
a21x1 + a22x2 +…+ a2nxn = b2 (2)
……………………………….
am1x1 + am2x2 +…+ amnxn = bm
Бұл жүйенің теңдеулеріндегі x1, x2, …, x n белгісіздерінің орнына табылған мәндерін қойғанда сол теңдеулерді тепе-теңдікке айналдыратын а 1, а 2, …, а n сандар жиынтығы сызықтық теңдеулер жүйесінің шешімдері деп аталады. Ал (2) сызықтық теңдеулер жүйесі негізгі матрицамен кеңейтілген матрицаның рангілерін салыстыру арқылы шешіледі. Егер олардың рангілері бір-бірімен дәл келсе, онда сызықтық теңдеулер жүйесі үйлесімді, ал кеңейтілген матрицаның рангісі негізгі матрицаның рангісінен үлкен болса, онда сызықтық теңдеулер жүйесі үйлесімсіз болады. Егер (2) сызықтық теңдеулер жүйесінің барлық b i мүшелері нөлге тең болса, онда сызықтық теңдеулер жүйесі бір текті деп аталады. Сызықтық теңдеулер жүйесінің бір шешімі, шексіз көп шешімі немесе мүлде шешімі болмауыда мүмкін. 1-дәрежелі теңдеуді шешу Хорезми еңбектерінде кездеседі. 1750ж. швейцарлық ғалым Г.Крамер (1704 – 1752) сызықтық теңдеулер жүйесін шешетін ереже тапты, ал 100 жылдан кейін неміс математигі Л.Кронекер (1823 – 1891) бұл теорияны жалпылап, аяқтады.
Иррационал теңдеулер - деп түбір таңбасы астында айнымалылары бар теңдеулер. Иррационал сандар– «ир» латынша кері мағыналы ұғымдарды атау үшін қолданылатын қосымша сөз, шектеусіз периодсыз ондық бөлшектер. Рационал сандар - m/n түріндегі сан, мұндағы m – рационал сан, n – натурал сан. Дискриминант – латынның discriminans – ажырату, анықтау деген сөзінен шыққан. Дискриминант таңбасына қарап отырып, оның неше түбірі бар екенін анықтайды (ажыратады). Биквадрат теңдеy – 〖ax〗^4+〖bx〗^2+c=0,a≠0 түрінде берілген теңдеу. Модуль таңбасы бар теңдеулер - айнымалысы модуль таңбасымен берілген теңдеулер. Параметрлі теңдеу –(грек тілінен орысшаға аударғанда - отмеривающий) f (х;а) = g(х;а) түріндегі бір айнымалысы бар (x - айнымалы, а - параметр) теңдеу. Виет теоремасы – келтірілген квадрат теңдеудің түбірін тез табу теоремасы. Түбірлерінің қосындысы қарама-қарсы таңбамен алынған екінші коэффициентке, ал түбірлерінің көбейтіндісі бос мүшеге тең. Теорема француз математигі Франсуа Виеттің құрметіне аталған. Алгебралық шартты белгілер жүйесін енгізген элементар алгебраның негізін қалаушы. Ол алғашқылардың бірі болып сандарды әріптермен белгілеуді енгізіп, теңдеулер теориясын едәуір дамытқан.
2-дәрежелі көпмүше немесе квадраттық теңдеу, квадраттық үшмүшелік деп
ax2+bx+c=0
түріндегі көпмүшелі теңдеуді айтамыз. Мұндағы a≠0 (Егер a = 0 болса, теңдеу ). Квадрат теңдеудің графигі - парабола (яғни квадрат функция).Квадрат теңдеу – 2-дәрежелі алгебралық теңдеу. Оның жалпы түрі мынадай: ax2+bx+c=0, a≠0. Квадрат үшмүшекомплекс сандаржиынында(с)сызықтық көбейткіштерге жіктеледі:
ax2+bx+c= a(x - x1)(х - x2),мұндағы х1.х2-ах2+bx+c=0 квадрат тендеудің түбірлері; х1. х2 — сандары квадрат үш мүшенің түбірлері деп те, сонымен қатар бұлар бұлар y=f(x)=ax2+bx+c квадрат функциясының нөлдері депте аталады. Квадрат үш мүшені мына түрде де жазуға болады:
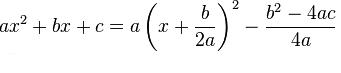
Осы өрнек нақтыайнымалыныңквадрат функциясының графигін салу кезінде функцияның ең үлкен(a>0 болғанда) немесе ең кіші (a>0 болғанда) мәндерін анықтау үшін пайдаланылады. ax2+bx+c квадрат функциясының графигі парабола болады, оның
н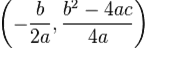 үктесінде орналасқан.
үктесінде орналасқан.
—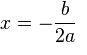
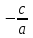 шаманы сол жаққа ауыстырсақ,
шаманы сол жаққа ауыстырсақ, 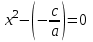 аламыз .
аламыз .Сонымен
 , содан кейін
, содан кейін 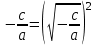 . Сондықтан
. Сондықтан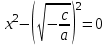 .
.Осы теңдеудің сол жағын көбейту арқылы біз
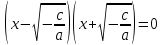 аламыз .
аламыз .Егер коэффициенттердің кем дегенде біреуі нөлге тең болса, бұл теңдік нөлге тең болады.
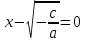 қарастырып,
қарастырып,  аламыз ;
аламыз ; 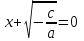 қарастырып,
қарастырып,  табамыз.
табамыз.Демек ,
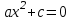 теңдеудің
теңдеудің  кезінде екі түбірі бар: ол
кезінде екі түбірі бар: ол  ,
,  . Жауап көбінесе
. Жауап көбінесе 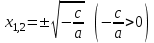 түрінде жазылады .
түрінде жазылады .Мысалы,
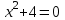 толық емес квадрат теңдеудің нақты түбірі жоқ. Толық емес
толық емес квадрат теңдеудің нақты түбірі жоқ. Толық емес 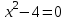 квадрат теңдеу үшін біз
квадрат теңдеу үшін біз 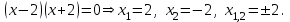 аламыз.
аламыз. Бұл теңдікті басқалай шешуге болады:
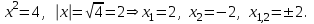
3.
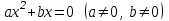 теңдеуді оның сол жағын көбейткіштерге бөлу арқылы шешуге болады. Әлбетте
теңдеуді оның сол жағын көбейткіштерге бөлу арқылы шешуге болады. Әлбетте 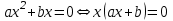 , осыдан
, осыдан  ,
, 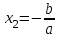 . Мысалы,
. Мысалы, 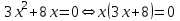 , осыдан
, осыдан ,
, 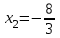 .
.Жалпы жағдайда квадрат теңдеулерді шешу үшін толық квадратты таңдау әдісі қолданылады. [5, c.120]
Бұл әдісті қолдану алдымен мысалдармен түсіндіріледі.
Мысал 1.
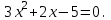 квадрат теңдеуді шешіңіз
квадрат теңдеуді шешіңізШешім. Теңдеудің екі бөлігін де 3 ке бөлейік :
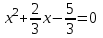
Толық квадратты таңдау әдісін қолданамыз:
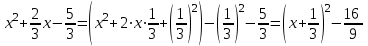 .
.Сондықтан біз
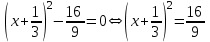 аламыз,
аламыз,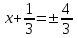 . Сондықтан,
. Сондықтан,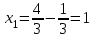 ,
, 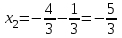 .
.Толық квадратты бастапқы теңдеуде және алдын-ала 3 ке бөлусіз бөлуге болады (белгісіз квадраттағы коэффициент):
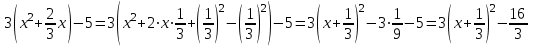 Сондықтан
Сондықтан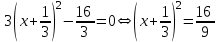 және т. б. [2, с.107]
және т. б. [2, с.107]Енді жалпы түрдің квадрат теңдеуін қарастырайық

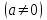 . (1)
. (1)Толық квадратты таңдау әдісін қолданамыз. Ол үшін теңдеудің сол жағын келесі түрде жазайық:
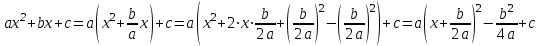
Сондықтан
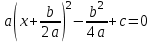 немесе
немесе 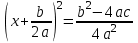 . (2)
. (2)Қосымша шешім алынған теңдеудің оң жағындағы белгіге байланысты (2).
Өйткені
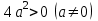 , оң жақ бөліктің белгісі
, оң жақ бөліктің белгісі 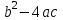 өрнек белгісімен сәйкес келеді . [15, c.163]
өрнек белгісімен сәйкес келеді . [15, c.163]Анықтама.
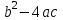 өрнек
өрнек 
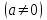 квадрат теңдеудің дискриминанты деп аталады және
квадрат теңдеудің дискриминанты деп аталады және 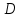 әріппен белгіленеді :
әріппен белгіленеді : 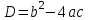 .
.Үш жағдайды қарастырайық:.
1.
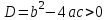 .
.Бұл жағдайда (2) теңдеуді келесідей жазуға болады:
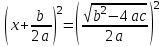 ;
;сондықтан,
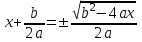
,
осыдан
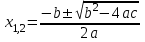 , (3)
, (3)немесе
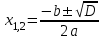 , (4)
, (4)мұндағы
 - теңдеудің дискриминанты (1).
- теңдеудің дискриминанты (1).2.
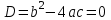 .
.Бұл жағдайда (2) теңдеу
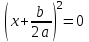 форманы алады,
форманы алады, Қайдан
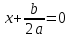 , яғни
, яғни 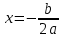 .
.Осылайша, егер дискриминант нөлге тең болса, яғни
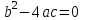 теңдеудің жалғыз түбірі
теңдеудің жалғыз түбірі 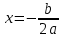 болады .
болады .3.
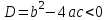 .
.Бұл жағдайда (2) теңдеудің оң жағында теріс сан, ал сол жағында теріс емес (оң немесе нөлге тең) болады. Сондықтан , егер
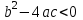 болса, онда (2) теңдеу, демек
болса, онда (2) теңдеу, демек  теңдеудің нақты түбірі жоқ.
теңдеудің нақты түбірі жоқ.Қорытынды.
 квадрат теңдеудің
квадрат теңдеудің 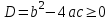 дискриминанты кезінде ғана нақты түбірі болады; егер
дискриминанты кезінде ғана нақты түбірі болады; егер 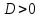 , онда түбірлер әр түрлі; егер
, онда түбірлер әр түрлі; егер 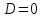 , онда түбірлер тең. Квадрат теңдеудің түбір формуласы (3) немесе (4) түрінде болады.
, онда түбірлер тең. Квадрат теңдеудің түбір формуласы (3) немесе (4) түрінде болады.Бұл формула бойынша толық емес квадрат теңдеулердің түбірлерін табуға болады, бірақ оларды көрсетілгендей толық емес квадрат теңдеудің сол жағын көбейту арқылы есептеу оңайырақ.
§4. Сызықтық және квадраттық теңдеулер
Екі айнымалысы бар сызықтық теңдеу: Бір айнымалысы бар сызықты теңдеу ах = в түрінде болады. Екі айнымалысы бар сызықты теңдеу ах + ву = с (1 ) түрінде беріледі,мұндағы х,у - айнымалылар, а,в,с – нақты сандар және а мен в бір мезгілде нөлге тең емес.
Мысалы: 2х + 3у = 8; 0,6х – 1,2у= 3;
Екі айнымалысы бар сызықтық теңдеуде әр қосылғыштағы айнымалылардың дәреже көрсеткіштерінің қосындысы 1- ге тең болуы керек. (1) теңдеуді қанағаттандыратын кез-келген сандар жұбы екі айнымалысы бар сызықтық теңдеудің шешімі деп аталады. Мыс: х+у=12 теңдеуінің шешімдер жұбы: (1;11), (5;7),,(9;3),(3;9) т.б Бір айнымалыны екіншісі арқылы өрнектеу үшін: 2у – х = 5 теңдеуінде х айнымалысын у айнымалысы арқылы өрнектейік. x = 2у – 5. Екі айнымалысы бар сызықтық теңдеудің ең болмағанда бір айнымалысының коэффициенті нөлге тең болмаса,оның графигі түзу сызық болады.
Екі айнымалысы бар сызықтық емес теңдеулер және оның шешімі: Егер теңдеулер құрамының біреуі сызықтық емес теңдеу болса,онда екі айнымалысы бар теңдеулер жүйесі екі айнымалысы бар сызықтық емес теңдеулер жүйесі деп аталады.
Мысал:
ж
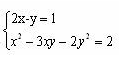 үйедегі бірінші теңдеудің графигі түзу сызық екені белгілі,ал екінші теңдеу графигін білмейміз. Мұндай жүйелерді шешудің негізгі жолы – ауыстыру тәсілі. Шешу алгоритмі:
үйедегі бірінші теңдеудің графигі түзу сызық екені белгілі,ал екінші теңдеу графигін білмейміз. Мұндай жүйелерді шешудің негізгі жолы – ауыстыру тәсілі. Шешу алгоритмі:1)бірінші дәрежелі теңдеуден айнымалының бірін екіншісі арқылы өрнектеп жазу;
2)табылған өрнекті екінші дәрежелі теңдеудегі айнымалының орнына қойып бір айнымалысы бар теңдеу аламыз;
3)шыққан теңдеуді шешкенде айнымалылардың біреуінің мәндері табылады;
4)Осы мәндер арқылы екінші айнымалының мәні табылады.
Егер айнымалылардың біреуінің коэффициенттері қарама-қарсы сандар болса мүшелеп қосу тәсілін қолданамыз.
Сызықтық теңдеу – белгісіздері (айнымалы шамалары) 1-дәрежелі болып келетін және белгісіздердің көбейтінділері қатыспайтын теңдеу.
Мысалы:
а1х1 + а2х2 +…+ + аnхn = b (1)
түріндегі теңдеу n белгісізі (аі≤0, і=1, 2, …, n) бар сызықтық теңдеуге жатады. Егер (1) теңдеудегі аi=0 (і=2, 3, …, n) болып, бірақ а1≤0 болса, онда ол а1х = b немесе ах = b (а1 = а) түріндегі бір белгісізі бар сызықтық теңдеуге айналады. Берілген айнымалыларға қатысты бірнеше сызықтық теңдеулер жиынтығы Сызықтық теңдеулер жүйесін құрады:
a11x1 + a12x2 +…+ a1nxn = b1
a21x1 + a22x2 +…+ a2nxn = b2 (2)
……………………………….
am1x1 + am2x2 +…+ amnxn = bm
Бұл жүйенің теңдеулеріндегі x1, x2, …, x n белгісіздерінің орнына табылған мәндерін қойғанда сол теңдеулерді тепе-теңдікке айналдыратын а 1, а 2, …, а n сандар жиынтығы сызықтық теңдеулер жүйесінің шешімдері деп аталады. Ал (2) сызықтық теңдеулер жүйесі негізгі матрицамен кеңейтілген матрицаның рангілерін салыстыру арқылы шешіледі. Егер олардың рангілері бір-бірімен дәл келсе, онда сызықтық теңдеулер жүйесі үйлесімді, ал кеңейтілген матрицаның рангісі негізгі матрицаның рангісінен үлкен болса, онда сызықтық теңдеулер жүйесі үйлесімсіз болады. Егер (2) сызықтық теңдеулер жүйесінің барлық b i мүшелері нөлге тең болса, онда сызықтық теңдеулер жүйесі бір текті деп аталады. Сызықтық теңдеулер жүйесінің бір шешімі, шексіз көп шешімі немесе мүлде шешімі болмауыда мүмкін. 1-дәрежелі теңдеуді шешу Хорезми еңбектерінде кездеседі. 1750ж. швейцарлық ғалым Г.Крамер (1704 – 1752) сызықтық теңдеулер жүйесін шешетін ереже тапты, ал 100 жылдан кейін неміс математигі Л.Кронекер (1823 – 1891) бұл теорияны жалпылап, аяқтады.
Иррационал теңдеулер - деп түбір таңбасы астында айнымалылары бар теңдеулер. Иррационал сандар– «ир» латынша кері мағыналы ұғымдарды атау үшін қолданылатын қосымша сөз, шектеусіз периодсыз ондық бөлшектер. Рационал сандар - m/n түріндегі сан, мұндағы m – рационал сан, n – натурал сан. Дискриминант – латынның discriminans – ажырату, анықтау деген сөзінен шыққан. Дискриминант таңбасына қарап отырып, оның неше түбірі бар екенін анықтайды (ажыратады). Биквадрат теңдеy – 〖ax〗^4+〖bx〗^2+c=0,a≠0 түрінде берілген теңдеу. Модуль таңбасы бар теңдеулер - айнымалысы модуль таңбасымен берілген теңдеулер. Параметрлі теңдеу –(грек тілінен орысшаға аударғанда - отмеривающий) f (х;а) = g(х;а) түріндегі бір айнымалысы бар (x - айнымалы, а - параметр) теңдеу. Виет теоремасы – келтірілген квадрат теңдеудің түбірін тез табу теоремасы. Түбірлерінің қосындысы қарама-қарсы таңбамен алынған екінші коэффициентке, ал түбірлерінің көбейтіндісі бос мүшеге тең. Теорема француз математигі Франсуа Виеттің құрметіне аталған. Алгебралық шартты белгілер жүйесін енгізген элементар алгебраның негізін қалаушы. Ол алғашқылардың бірі болып сандарды әріптермен белгілеуді енгізіп, теңдеулер теориясын едәуір дамытқан.
2-дәрежелі көпмүше немесе квадраттық теңдеу, квадраттық үшмүшелік деп
ax2+bx+c=0
түріндегі көпмүшелі теңдеуді айтамыз. Мұндағы a≠0 (Егер a = 0 болса, теңдеу ). Квадрат теңдеудің графигі - парабола (яғни квадрат функция).Квадрат теңдеу – 2-дәрежелі алгебралық теңдеу. Оның жалпы түрі мынадай: ax2+bx+c=0, a≠0. Квадрат үшмүшекомплекс сандаржиынында(с)сызықтық көбейткіштерге жіктеледі:
ax2+bx+c= a(x - x1)(х - x2),мұндағы х1.х2-ах2+bx+c=0 квадрат тендеудің түбірлері; х1. х2 — сандары квадрат үш мүшенің түбірлері деп те, сонымен қатар бұлар бұлар y=f(x)=ax2+bx+c квадрат функциясының нөлдері депте аталады. Квадрат үш мүшені мына түрде де жазуға болады:
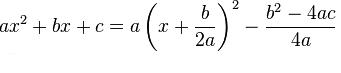
Осы өрнек нақтыайнымалыныңквадрат функциясының графигін салу кезінде функцияның ең үлкен(a>0 болғанда) немесе ең кіші (a>0 болғанда) мәндерін анықтау үшін пайдаланылады. ax2+bx+c квадрат функциясының графигі парабола болады, оның
н
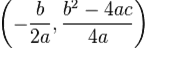 үктесінде орналасқан.
үктесінде орналасқан.—