ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 04.02.2024
Просмотров: 30
Скачиваний: 0
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
түзуі параболаның симметрия осі болып табылады. a>0 болғанда параболаның тармақтары жоғары карай, a<0 болғанда — төмен қарай бағытталады. a<0 болғанда x=(-b)/2a нүктесінде максимумға кетерілсе, ал a>0 болғанда y=(b2-4ac)/4a нүктесінде минимумға төмендейді.
Парабола ордината осін (0,b) нүктелерінде қиып өтеді. Егер квадрат үшмүшенің нақты түбірлері x1≠x2 болса, онда парабола абсцисса осін (x1,0) және (x2,0)нүктелерінде қиып өтеді, x=x2 болса, парабола абсцисса осімен (x1,0) нүктесінде жанасады. a, b, және c әріптері - коэффиценттер деп аталады: a квадраттық коэффиценті - x2-тың коэффиценті, b коэффиценті - x-тің коэффиценті, ал c - тұрақты коэффицент немесе тұрақты мүше.
§5. Үшінші дәрежелі теңдеулер
Орта ғасырлар заманында алгебра, алгебралық символика бойынша жинақталған мағұлматттар, қол жеткен табыстар нəтижесінде XYI ғасырдың математиктері күн тəртібіне бұрыннан қойылған, көптен бері шешуі табылмай келе жатқан бірсыпыра ірі мəселелерді қолға алды. Солардың бірі үшінші əне төртінші дəрежелі теңдеулерді шешу үшін қортып шығару.
Ариметика мен алгебра саласында үнділер ірі табысқа жетті. Үнділердің математикалық шығармалары біздің эрамыздың VI-XII ғасырлары арасында жазылған.
Үнді математиктері үшінші жəне төртінші дəрежелі теңдеуге келтірілетін кейбір есептерді шеше білген. Бірақ жалпы формуласын білмеген. Біздің қарастыратынымыз
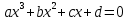
түрінде берілген үшінші дәрежелі теңдеу. Енді осы теңдеудің түбірін табудың бірнеше тәсілін қарастырайық. Соның бірі мектеп оқулығында кездесетін топтау тәсілі.
Мысалы:
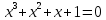
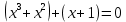
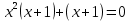
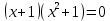
бұдан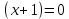 ,
, 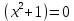
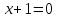 ,
, 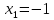
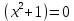
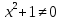 бола алмайды, сондықтан бұл теңдеудің тек қана бір
бола алмайды, сондықтан бұл теңдеудің тек қана бір
 шешімі ғана бар.
шешімі ғана бар.
Біз үшінші дәрежелі теңдеулерді шешудің оқулықтағы топтастыру әдісінен басқа Безу теоремасы, Кардано формуласы, Виет теоремасы арқылы шешу әдіс - тәсілдерін де оқушыларға меңгерте білуіміз керек. Бұл әдістер мектеп оқулығында жазылмағанымен оқушылардың шығармашылығын дамыту негізінде орыс тіліндегі альтернативті кітаптарды пайдаланатын ұстаздар қауымыда бар. Міне сол себептен есептеудің стандарттық тәсілінен өзге нұсқалары барлық оқушыларға қол жетімді болатындай мектеп оқулықтарына қосымша құрал ретінде енгізілгені жөн.
Енді солардың бірі Виет теоремасы бойынша:
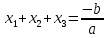 ,
,
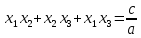 ,
,
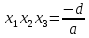 .
.
Көрсетілген тепе – теңдіктерді бір – біріне бөлудің нәтижесінде тағы да басқа арақатынастар табуға болады:
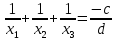 ,
, 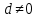 ,
,
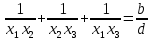 ,
, 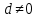 .
.
Жоғарыдағы мысалдың түбірлерін табуды Виет теоремасы бойынша анықтайық.
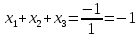 ,
,
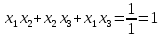 ,
,
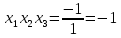 .
.
Ал дискриминант табу арқылы шешуде:
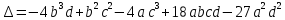 .
.
*Егер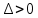 болса, онда теңдеудің үш әр түрлі түбірі болады.
болса, онда теңдеудің үш әр түрлі түбірі болады.
*Егер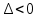 болса, онда теңдеудің бір нақты және екі комплексті түйіндес түбірі болады.
болса, онда теңдеудің бір нақты және екі комплексті түйіндес түбірі болады.
*Егер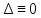 болса, онда теңдеудің екі түбірі болсын сәйкес келеді.
болса, онда теңдеудің екі түбірі болсын сәйкес келеді.
Безу теоремасы
Безу теоремасы P(x) көпмүшелігін x-a екі мүшелікке бөлгендегі қалдық P(a)-ға тең деп тұжырымдайды.
Көпмүшелік коэффициенттері белгілі бір коммутативті бірлігі бар сақинада (мысалы, нақты сандар немесе комплекс сандар өрісінде) жатыр деп саналады.
Дәлелдеу
P(x) көпмүшелігін қалдықпен x-a көпмүшелігіне бөлейік:
P(x)=( x-a)Q(x)+R(x).
degR(x)
Салдары
Кардано формуласы
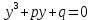
Түріндегі кубтық теңдеудің түбірлерін комплекс сандар өрісінде табуға арналған формула. Оның өрнектелуі мынадай: Кардано формуласындағы куб түбірлердің мәндерін, олардың көбейтіндісі –р/3 –ге тең болатындай етіп алу керек. Ал теңдеудің түбірлерін табу үшін осы мәндерді қосу қажет. Осы жолмен теңдеудің үш түбірі табылады. Кардано формуласы италиялық математик, филосо әрі дәрігер Дж.Кардано(1501-1576) есімімен аталған. Ол оны алғаш рет 1545 жылы жариялаған. Жалпы түрдегі кез келген кубтық теңдеу

Жоғарыда көрсетілген келтірілген түрде коэффициенттері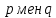 болатындай жазыла алады:
болатындай жазыла алады:
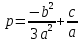
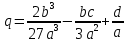
Керекті мына түрдегі х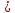 у-а айнымалы ауыстыруымен.
у-а айнымалы ауыстыруымен.
Соңғы үшеуін кубтық теңдеуге қойып мынаны табамыз:
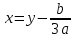
Формуласы
Q деп:
Q=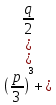 белгілейік.
белгілейік.
Егер кубтық теңдеудің барлық коэффициенттері нақты болса, онда Q да нақты сан болады, ал оның таңбасымен түбірлерінің түрлерін білуге болады:
Кардано формуласы бойынша, кубтық теңдеудің түбірлері келтірілген түрінде:
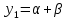 ,
,
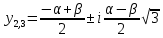 6
6
Мұндағы
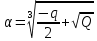 ,
, 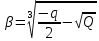 ,
,
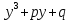 көпмүшеліктің дискриминанты бұл жағдайда -
көпмүшеліктің дискриминанты бұл жағдайда -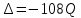 .
.
Осы формулаларды пайдалана,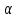 -ның әр үш мәні үшін
-ның әр үш мәні үшін 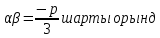 алтындай
алтындай 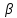 мәні әрқашан болады. Егер кубтық теңдеу нақты боса,онда мүмкіндігінше нақты
мәні әрқашан болады. Егер кубтық теңдеу нақты боса,онда мүмкіндігінше нақты 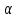 ,
,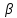 алған дұрыс.
алған дұрыс.
Үшінші дәрежелі теңдеулерді шешудің түрлі әдістерінен байқағанымыз есептер математикалық білім, білік дағды жүйесін қалыптастырудың маңызды құралы, ал есеп шығару - оқу және кәсіптік әрекеттің жетекші түрі дер едік. Әрбір есептің өзіндік әдістемелік мақсаты да бар. Сондықтан оқушы есепті жылдам әрі қатесіз шығаруға, жаттыға түсуге ұмтыла отырып, оны шығармашылықпен шешуге, шешімінен тиісті қорытынды жасай білуге тырысуы қажет. Математиканы үйренумен белсенді шұғылдану, шын мәнінде, есеп шығару дер едім. Себебі болашақ ғалымдар – бүгінгі күннің оқушылары, ертеңгі өрелі ізденістерді бүгіннен бастап білуі керек. Міне сондықтанда “Бала бақыты – жақсы ұстаз қолында” деген сөздің түп негізі осында жатқан сияқты.
0>0>0>
§6. Төртінші дәрежелі теңдеулер
Алдымен төртінші дәрежелі алгебралық теңдеуді шешудің Феррари әдісіне тоқталайық. Төртінші дәрежелі алгебралық теңдеу мына түрде жазылады:
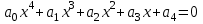 , (1)
, (1)
мұндағы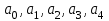 – кезкелген нақты сандар, әрі
– кезкелген нақты сандар, әрі 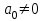 .
.
Феррари әдісі екі бөліктен тұрады..
Бірінші бөлікте (1) түріндегі теңдеу белгісіздің үшінші дәрежесі жоқ төртінші дәрежелі «толық емес» теңдеуге келтіріледі.
Екінші бөлікте алынған теңдеу оның сол жақ бөлігін көбейткіштерге жіктеу арқылы шешіледі. Қажетті жіктелуді алу үшін үшінші дәрежелі теңдеуді шешуге тура келеді.
Феррари әдісінің бірінші бөлігі. Төртінші дәрежелі теңдеуді «толық емес» теңдеуге келтірейік. Ол үшін (1) теңдеуді бас мүшеге бөлеміз. Сонда ол мына түрге келеді:
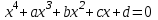 , (2)
, (2)
мұндағы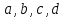 – нақты сандар.
– нақты сандар.
(2) теңдеуде
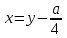 ,
,
мұндағы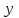 – жаға белгісіз, ауыстыруын жасаймыз. Сонда
– жаға белгісіз, ауыстыруын жасаймыз. Сонда
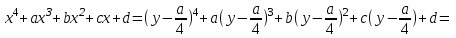
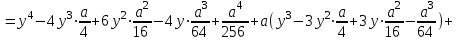
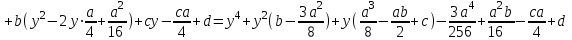
болғандықтан, (2) теңдеу мына түрге келеді:
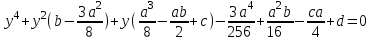 . (4)
. (4)
Егер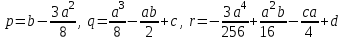 белгілеулерін енгізсек, (4) теңдеуді мына түрде жаза аламыз:
белгілеулерін енгізсек, (4) теңдеуді мына түрде жаза аламыз:
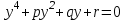 , (5)
, (5)
мұндағы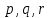 – нақты сандар.
– нақты сандар.
Феррари әдісінің екінші бөлігі. (5) теңдеудің сол жақ бөлігін көбейткіштерге жіктейік. Ол үшін (5) теңдеудің сол жақ бөлігіне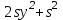 мұндағы
мұндағы 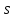 – кейінірек анықталатын қандай да бір сан, өрнегін қосып, алып тастаймыз. Сонда
– кейінірек анықталатын қандай да бір сан, өрнегін қосып, алып тастаймыз. Сонда
Парабола ордината осін (0,b) нүктелерінде қиып өтеді. Егер квадрат үшмүшенің нақты түбірлері x1≠x2 болса, онда парабола абсцисса осін (x1,0) және (x2,0)нүктелерінде қиып өтеді, x=x2 болса, парабола абсцисса осімен (x1,0) нүктесінде жанасады. a, b, және c әріптері - коэффиценттер деп аталады: a квадраттық коэффиценті - x2-тың коэффиценті, b коэффиценті - x-тің коэффиценті, ал c - тұрақты коэффицент немесе тұрақты мүше.
§5. Үшінші дәрежелі теңдеулер
Орта ғасырлар заманында алгебра, алгебралық символика бойынша жинақталған мағұлматттар, қол жеткен табыстар нəтижесінде XYI ғасырдың математиктері күн тəртібіне бұрыннан қойылған, көптен бері шешуі табылмай келе жатқан бірсыпыра ірі мəселелерді қолға алды. Солардың бірі үшінші əне төртінші дəрежелі теңдеулерді шешу үшін қортып шығару.
Ариметика мен алгебра саласында үнділер ірі табысқа жетті. Үнділердің математикалық шығармалары біздің эрамыздың VI-XII ғасырлары арасында жазылған.
Үнді математиктері үшінші жəне төртінші дəрежелі теңдеуге келтірілетін кейбір есептерді шеше білген. Бірақ жалпы формуласын білмеген. Біздің қарастыратынымыз
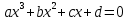
түрінде берілген үшінші дәрежелі теңдеу. Енді осы теңдеудің түбірін табудың бірнеше тәсілін қарастырайық. Соның бірі мектеп оқулығында кездесетін топтау тәсілі.
Мысалы:
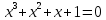
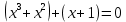
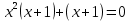
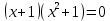
бұдан
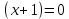 ,
, 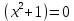
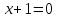 ,
, 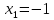
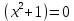
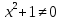 бола алмайды, сондықтан бұл теңдеудің тек қана бір
бола алмайды, сондықтан бұл теңдеудің тек қана бір
 шешімі ғана бар.
шешімі ғана бар.Біз үшінші дәрежелі теңдеулерді шешудің оқулықтағы топтастыру әдісінен басқа Безу теоремасы, Кардано формуласы, Виет теоремасы арқылы шешу әдіс - тәсілдерін де оқушыларға меңгерте білуіміз керек. Бұл әдістер мектеп оқулығында жазылмағанымен оқушылардың шығармашылығын дамыту негізінде орыс тіліндегі альтернативті кітаптарды пайдаланатын ұстаздар қауымыда бар. Міне сол себептен есептеудің стандарттық тәсілінен өзге нұсқалары барлық оқушыларға қол жетімді болатындай мектеп оқулықтарына қосымша құрал ретінде енгізілгені жөн.
Енді солардың бірі Виет теоремасы бойынша:
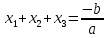 ,
,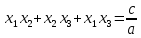 ,
,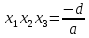 .
.Көрсетілген тепе – теңдіктерді бір – біріне бөлудің нәтижесінде тағы да басқа арақатынастар табуға болады:
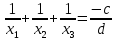 ,
, 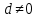 ,
,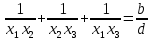 ,
, 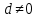 .
.Жоғарыдағы мысалдың түбірлерін табуды Виет теоремасы бойынша анықтайық.
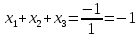 ,
,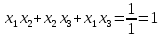 ,
,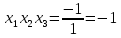 .
.Ал дискриминант табу арқылы шешуде:
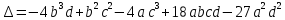 .
.*Егер
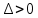 болса, онда теңдеудің үш әр түрлі түбірі болады.
болса, онда теңдеудің үш әр түрлі түбірі болады.*Егер
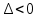 болса, онда теңдеудің бір нақты және екі комплексті түйіндес түбірі болады.
болса, онда теңдеудің бір нақты және екі комплексті түйіндес түбірі болады.*Егер
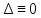 болса, онда теңдеудің екі түбірі болсын сәйкес келеді.
болса, онда теңдеудің екі түбірі болсын сәйкес келеді.Безу теоремасы
Безу теоремасы P(x) көпмүшелігін x-a екі мүшелікке бөлгендегі қалдық P(a)-ға тең деп тұжырымдайды.
Көпмүшелік коэффициенттері белгілі бір коммутативті бірлігі бар сақинада (мысалы, нақты сандар немесе комплекс сандар өрісінде) жатыр деп саналады.
Дәлелдеу
P(x) көпмүшелігін қалдықпен x-a көпмүшелігіне бөлейік:
P(x)=( x-a)Q(x)+R(x).
degR(x)
Салдары
-
а саны сонда тек сонда,егер р(х) қалдықсыз х-а –ға бөлінсе р(х) көпмүшелігінің түбірі болады (осыдан Р(х) көпмүшелігінің түбірлер жиыны сәйкес Р(х) =0 теңдеуінің шешімдер жиынымен бірдей). -
Бүтін коэффициентті көпмүшеліктің бос мүшесі көпмүшеліктің кез келген бүтін түбіріне қалдықсыз бөлінеді(егер жоғарғ коэффициентті 1 болса, онда барлық рационал түбірлері де бүтін болады). -
а –бүтін коэффициентті А(х) келтірілген көпмүшеліктің бүтін түбірі болсы. Онда кез келген бүтін к саны үшін А(к) саны а-к санына бөлінеді.
Кардано формуласы
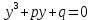
Түріндегі кубтық теңдеудің түбірлерін комплекс сандар өрісінде табуға арналған формула. Оның өрнектелуі мынадай: Кардано формуласындағы куб түбірлердің мәндерін, олардың көбейтіндісі –р/3 –ге тең болатындай етіп алу керек. Ал теңдеудің түбірлерін табу үшін осы мәндерді қосу қажет. Осы жолмен теңдеудің үш түбірі табылады. Кардано формуласы италиялық математик, филосо әрі дәрігер Дж.Кардано(1501-1576) есімімен аталған. Ол оны алғаш рет 1545 жылы жариялаған. Жалпы түрдегі кез келген кубтық теңдеу

Жоғарыда көрсетілген келтірілген түрде коэффициенттері
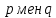 болатындай жазыла алады:
болатындай жазыла алады: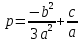
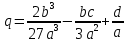
Керекті мына түрдегі х
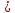 у-а айнымалы ауыстыруымен.
у-а айнымалы ауыстыруымен.Соңғы үшеуін кубтық теңдеуге қойып мынаны табамыз:
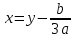
Формуласы
Q деп:
Q=
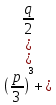 белгілейік.
белгілейік.Егер кубтық теңдеудің барлық коэффициенттері нақты болса, онда Q да нақты сан болады, ал оның таңбасымен түбірлерінің түрлерін білуге болады:
-
Q>0 –бір нақты түбір және екі түйіндес түбірлер. -
Q=0 – бір еселік түбір және екі еселік түбірлер , немесе , егер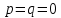 , онда бір үш еселік нақты түбір.
, онда бір үш еселік нақты түбір. -
Q<0 –үш нақты түбір. Бұл “келтірілмейтін” жағдай, дәл осы жағдайды зерттеу кезінде алғашқы рет комплекс сан ұғымы пайда болды.
Кардано формуласы бойынша, кубтық теңдеудің түбірлері келтірілген түрінде:
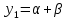 ,
,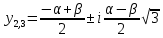 6
6Мұндағы
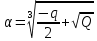 ,
, 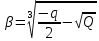 ,
,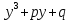 көпмүшеліктің дискриминанты бұл жағдайда -
көпмүшеліктің дискриминанты бұл жағдайда -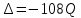 .
.Осы формулаларды пайдалана,
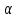 -ның әр үш мәні үшін
-ның әр үш мәні үшін 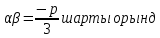 алтындай
алтындай 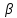 мәні әрқашан болады. Егер кубтық теңдеу нақты боса,онда мүмкіндігінше нақты
мәні әрқашан болады. Егер кубтық теңдеу нақты боса,онда мүмкіндігінше нақты 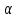 ,
,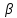 алған дұрыс.
алған дұрыс.Үшінші дәрежелі теңдеулерді шешудің түрлі әдістерінен байқағанымыз есептер математикалық білім, білік дағды жүйесін қалыптастырудың маңызды құралы, ал есеп шығару - оқу және кәсіптік әрекеттің жетекші түрі дер едік. Әрбір есептің өзіндік әдістемелік мақсаты да бар. Сондықтан оқушы есепті жылдам әрі қатесіз шығаруға, жаттыға түсуге ұмтыла отырып, оны шығармашылықпен шешуге, шешімінен тиісті қорытынды жасай білуге тырысуы қажет. Математиканы үйренумен белсенді шұғылдану, шын мәнінде, есеп шығару дер едім. Себебі болашақ ғалымдар – бүгінгі күннің оқушылары, ертеңгі өрелі ізденістерді бүгіннен бастап білуі керек. Міне сондықтанда “Бала бақыты – жақсы ұстаз қолында” деген сөздің түп негізі осында жатқан сияқты.
0>0>0>
§6. Төртінші дәрежелі теңдеулер
Алдымен төртінші дәрежелі алгебралық теңдеуді шешудің Феррари әдісіне тоқталайық. Төртінші дәрежелі алгебралық теңдеу мына түрде жазылады:
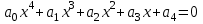 , (1)
, (1)мұндағы
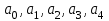 – кезкелген нақты сандар, әрі
– кезкелген нақты сандар, әрі 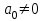 .
. Феррари әдісі екі бөліктен тұрады..
Бірінші бөлікте (1) түріндегі теңдеу белгісіздің үшінші дәрежесі жоқ төртінші дәрежелі «толық емес» теңдеуге келтіріледі.
Екінші бөлікте алынған теңдеу оның сол жақ бөлігін көбейткіштерге жіктеу арқылы шешіледі. Қажетті жіктелуді алу үшін үшінші дәрежелі теңдеуді шешуге тура келеді.
Феррари әдісінің бірінші бөлігі. Төртінші дәрежелі теңдеуді «толық емес» теңдеуге келтірейік. Ол үшін (1) теңдеуді бас мүшеге бөлеміз. Сонда ол мына түрге келеді:
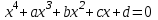 , (2)
, (2)мұндағы
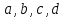 – нақты сандар.
– нақты сандар.(2) теңдеуде
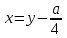 ,
, мұндағы
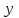 – жаға белгісіз, ауыстыруын жасаймыз. Сонда
– жаға белгісіз, ауыстыруын жасаймыз. Сонда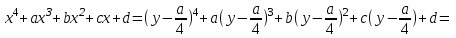
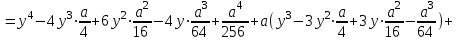
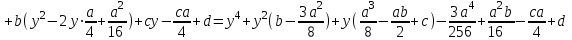
болғандықтан, (2) теңдеу мына түрге келеді:
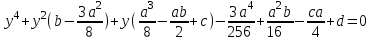 . (4)
. (4)Егер
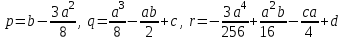 белгілеулерін енгізсек, (4) теңдеуді мына түрде жаза аламыз:
белгілеулерін енгізсек, (4) теңдеуді мына түрде жаза аламыз: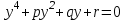 , (5)
, (5)мұндағы
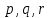 – нақты сандар.
– нақты сандар.Феррари әдісінің екінші бөлігі. (5) теңдеудің сол жақ бөлігін көбейткіштерге жіктейік. Ол үшін (5) теңдеудің сол жақ бөлігіне
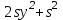 мұндағы
мұндағы 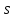 – кейінірек анықталатын қандай да бір сан, өрнегін қосып, алып тастаймыз. Сонда
– кейінірек анықталатын қандай да бір сан, өрнегін қосып, алып тастаймыз. Сонда

