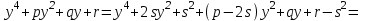
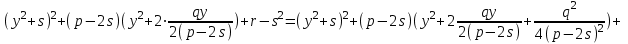
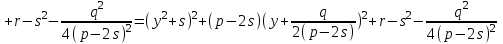
болады. Демек, (5) теңдеу мына түрге келеді:

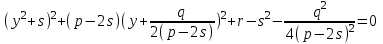. (6)

Егер санын

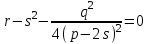(7)

теңдеуін қанағаттандыратындай етіп таңдап алсақ, онда (6) теңдеуді мына түрде жаза аламыз:

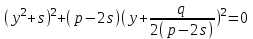. (8)

(7) теңдеуді бөлшектен құтылу арқылы мына түрде жазуға болады:

. (9)

Алынған кубтық теңдеу (7) теңдеуге эквивалентті және (5) теңдеудің кубтық резольвентасы деп аталады. Егер (9) теңдеудің қандай да бір шешімі табылған болса, онда (8) теңдеуді көбейткіштерге жіктеу арқылы шешуге болады:

.

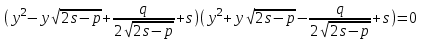Сонымен, (8) теңдеуді шешу үшін төмендегі екі квадрат теңдеуді шешу қажет екен:

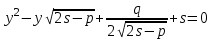, (10)

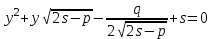. (11)

§7. Құрамында параметрі бар квадраттық теңдеулер

ax2+bx+c=0 теңдеуі квадраттық теңдеу деп аталады, мұндағы a,b,c тұрақты сандар ал x белгісіз айнымалы.

Жиын ұғымы. Жиынның элементтері

Жиын ұғымы математикада негізгі (анықтауға болмайтын, бастапқы) ұғым болып саналады. Сондықтан оны тек мысылдармен ғана түсіндіруге болады. Мысалы, қайсыбір класс оқушыларының жиыны туралы, Әлемдегі планеталар жиыны туралы айтуға болады. Жиын сөзі математикада жиынтық, класс, жинақ, коллекция деген сөздердің, яғни қайсыбір нәрселер жиынтығын сипаттайтын сөздердің орнына қолданылады, оның үстіне қарастырылып отырған жиынтықты бір ғана нәрсе болуы немесе бірде-бір нәрсе болмауы мүмкін.

Жиын құратын кез-келген нәрселер (адамдар, үйлер, кітаптар, елдер, геометриялық фигуралар, сандар т. б.) оның элементтері деп аталады. Мысалы, 3 саны — бір таңбалы натурал сандар жиынының элементі. Жиын мен оның элементтерінің арасындағы элементті болады деген байланысты тиісті сөзінің көмегімен де білдіруге болады. Мысалы, 3 саны бір таңбалы натурал сандар жиынына тиісті деп айтуға болады. Соңғы сөйлемде символдың көмегімен қысқаша жазуға болады: 3

---

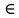А. Бұл жазуда А әрпі арқылы бір таңбалы натурал сандар жиыны белгіленген (жиынды латын алфавитінің бас әріптерімен белгілейді), ал 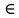белгісі тиісті сөзін алмастырады. Жалпы а 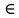А жазуы а нәрсесі А жиынының элементті, немесе а нәрсесі А жиынына тиісті, немесе А жиынында а элементі бар деп оқылады. а 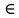А жазуына нәрсесі А жиынына тиісті емес, немесе А жиынында а элементті жоқ, немесе а нәрсесі А жиынының элементі емес деп оқуға болады. Жиын элементтерінің саны шектеулі де, шектеусіз болуы мүмкін. Мысалы, қайсыбір педучилище оқушыларының жиының элементтерінің саны шектеулі, ал түзудегі нүктелер жиыны шектеусіз.

Жиын ұғымы және онымен байланысты басқа да ұғымдар математиканы алғаш оқытудың негізі болады және онда кеңінен пайдаланылады. Кейбір оқулықтарда жиын термині кездеспейді, бірақ бұл ұғым айқындалмаған түрде пайдаланылады, ал бір қатар эксперимент кітаптарда жиын ұғымы символикасымен қоса айқын түрде пайдалалынылады. Сан, натурал сандарды қосу және көбейту амалдары және олардың қасиеттері, геометриялық фигура сияқты маңызды ұғымдардың қалыптасуы мектептегі математика курсында теориялық — жиындық негізде жүзеге асады.

Жиындардың жазылуы мен оның берілу тәсілдері.

Егер әрбір нәрсе туралы оның жиынға тиісті немесе тиісті емес екендігін айта алатын болсақ, онда жиын берілген деп саналады. Жиынды оның барлық элементтерін атау арқылы анықтап беруге болады. Егерде а, b, c, d — әр түрлі нәрселердің белгіленулері болса, онда осы нәрселердің жиынын А={ а, b, c, d } түрінде жазып, оны А жиыны а, b, c, d элементтерінен тұрады деп оқиды. Әрбір нәрсе жиынға тек бір рет қана енеді. Мысалы, 32 545 882 санының әр түрлі цифрларынан тұратын жиын {3, 2, 5, 4, 8}, ал есеп деген сөздегі әр түрлі әріптер жиыны {e, c, п} түрінде жазылады.

Жиынның берілуінің тағы бір тәсілі оны құрайтын нәрселердің ортақ қасиетін атау болып табылады. Мұндай қасиетті cипаттамалық қасиет деп атайды. Мысалға, 7-ден кем натурал сандардың А жиынын қарастырайық. Бұл жерде А жиынының барлық элементтерінің ортақ қасиеті, атап айтқанда, олардың натурал және 7-ден кіші сан болуы аталып отыр. Қарастырылып отырған А жиынының элементтерін атап шығу қиындыққа түспейді: А={1, 2, 3,4, 5, 6}. Жиынның осылай берілу тәсілі математикада жиі қолданылады. Мысалға радиусы r, центрі О болатын шеңбердің центрі О және радиусы r болатын шеңбер деп жазықтықтың О нүктесінен r қашықтықта жататын нүктелер жиынын атайды деген анықтамасын еске түсірейік. О-дан r қашықтықта және бір жазықтықта жату — центрі О және радиусы r болатын шеңбердің барлық нүктелеріне тән қасиет және бұл қасиетке шеңберге тиісті емес бірде бір нүкте ие бола алмайды.

---

Элементтердің сипаттамалық қасиеті көрсетілген жиынды былай жазуға болады: фигуралық жақшалар ішіне алдымен элементтерінің белгіленуін жазады. Содан кейін вертикаль сызықша қояды да сызықшадан соң осы жиын элементтеріне және тек соларға ғана тән қасиетті жазады. Мысалы, 7-ден кіші натурал сандар жиыны А былайша жазылады:

А={xx- натурал сан, x7}

Сонымен, қандай да бір жиын берілген болуы үшін не оның элементтерін атап шығу, не оның элементтеріне тән қасиетті көрсету керек. Екінші тәсіл біріншіге қарағанда жалпылау екенін айта кетеміз. Мәселе мынада: жиынның элементтерін атап шығу осы жиын шектеулі болғанда ғана мүмкін, ал жиын элементтерінің ортақ қасиетін жиын шектеулі болғанда ғана мүмкін, ал жиынэлементтерінің ортақ қасиетін жиын шектеулі болса да, шектеусіз болса да көрсетуге болады. Бірақ кейбір кезде шектеусіз жиынды да бірінші тәсілді пайдаланып жазыпкөрсетуге болады. Мысалы, барлық натурал сандар жиынын N әрпі арқылы белгілеп мына түрде N= {1, 2, 3, 4, …} жазуға болады. Әрине жиынды тек көп нүктелер орнында не болатыны белгілі жағдайда ғана осы түрде жазуға болады. Барлық натурал сандардан және нольден тұратын жиынды N0 арқылы белгілеп, былай жазады:

N0={1, 2, 3, 4, …}

Бұл жиынды оң бүтін сандар жиыны деп атайды. Барлық бүтін сандар жиынын Z әрпі арқылы белгілеу келісілген: Z={…, -5,-4, -3, -2, -1, 0, 1, 2, 3, 4, 5…}

Математиканы оқып-үйрену барысында шешуге тура келетін көптеген есептер элементтерінің ортақ қасиеті көрсетілген жиынды табумен байланысты болады.

Бірнеше мысалдар келтірейік.

1-мысал.

х(х-1)=0 теңдеуінің барлық түбірлерінің жиынын табу керек.

Ізделінді А жиынының барлық элементтеріне тән ортақ қасиет -х(х-1)=0 теңдеуінің түбірі болу, яғни А жиынын А={x x(x-1)=0} түрінде жазуға болады. x(x-1)=0 — теңдеуін шешеміз. Екі х және х-1 сандарының көбейтіндісі, тек сол сандардың біреуі ноль болғанда ғана, нольге тең болатындықтан х1=0, х2=1 екендігін табамыз. Демек, А={0, 1}.

1-есеп. Теңдеуді шешіңіз: 3х2–х+18=0.

Шешуі. aх2–bх+c=0 квадраттық теңдеуінің дискриминанты формуласымен есептеледі. Егер ол оң болса, теңдеудің екі түбірі бар болады да, формуласымен анықталады; егер де дискриминант нөлге тең болса, онда теңдеудің бір ғана түбірі бар болады да, ол формуласымен анықталады; ал егер дискриминант теріс болса, онда теңдеудің нақты түбірлері болмайды. Біздің жағдайымызда ,сондықтан теңдеудің түбірі жоқ.

Жауабы. Түбірі жоқ.

2-есеп. Теңдеуді шешіңіз: 3х²–14х+16=0.

Жауабы. 2; 2.

3-есеп. Теңдеуді шешіңіз: 4х

---

²–36х+77=0.

Жауабы. 3,5; 5,5.

4-есеп. Теңдеуді шешіңіз: 25х²=10х–1.

Шешуі. 25х²=10х–1; 25х²–10х+1=0. Теңдеудің сол жағы толық квадрат

екенін байқасақ: (5х–1)2=0; 5х–1=0; х=1: 5=0,2.

Жауабы. 0,2.

5-есеп. Теңдеуді шешіңіз: 6х(2х+1)=5х+1.

Шешуі. Алдымен теңдеуді түрлендіріп, квадраттық теңдеуге келтіріп

аламыз: 6х(2х+1)=5х+1; 12х²+6х=5х +1; 12х²+х-1=0. Дискриминант .

6-есеп. Теңдеуді шешіңіз: 2х(х – 8)= –х–18.

Жауабы. 1,5; 6.

7-есеп. (х+2)(х+4)=0 квадрат теңдеуінің шешімдерін көрсетіңіз.

Шешуі. (х+2)(х+4)=0; көбейтінді нөлге тең болуы үшін көбейткіштердің

ең болмағанда біреуі нөлге тең болуы керектігін пайдалана отырып,

көбейткіштерді жеке-жеке нөлге теңестіреміз:

1) х+2=0; х=–2;

2) х+4=0; х=–4.

Жауабы. –2; –4.

8-есеп. х²+6х+8 =0 теңдеуінің түбірлерін табыңыз.

Жауабы. –4; –2.

9-есеп. (х+3)(х–4)= –12 теңдеуінің түбірлерін табыңыз.

Шешуі. (х+3)(х–4)=–12; x²–4x+3х–1 2=–12; x2–x=0. Толымсыз квадратты теңдеу алдық, оны көбейткіштерге жіктеу тәсілімен шешеміз: х(х–1)=0;

Жауабы. 0; 1.

Қорытынды

Теориялық және эмпирикалық зерттеулердің нәтижелері қазіргі мектепте Алгебралық теңдеулерді зерттеудің ұсынылған әдістемесін және оларды шешу жолдарын қолдануға мүмкіндік бар деген болжам жасауға мүмкіндік берді. Бұл оқушыларды бастапқы ұғымдарды, математика негіздерін қабылдауға, оларды практикалық іс-әрекетте қолдануға дайындауды қамтамасыз етеді. Сондықтан оқушылардан математикалық ұғымдарды терең білуді талап ететін, оқушыларға жаңа жолдарды, жаңа мүмкіндіктерді, жаңа тәсілдерді іздеуге және дәстүрлі түрде де, стандартты емес жолмен де өмірлік маңызды мәселелерді шешуге деген ұмтылысты сіңіретін білім беруді дамытудың заманауи тенденцияларын ескеретін мектеп математикасы курсының сұрақтары үлкен маңызға ие.

Жұмысымыздың нәтижелеріне сүйене отырып, біз алгебралық теңдеулерді оқу процесі оқушыларды түсінуге қол жетімді, олардың білім сапасы мен математикадан білім деңгейін арттыруға ықпал ете алады, көптеген есептерді шешуге арналған қуатты математикалық аппаратпен қаруландырады деген қорытындыға келдік.

Жоғарыда айтылғандарға байланысты біз мектеп мұғалімдеріне оқушылардың шығармашылық қабілеттері мен логикалық ойлауын дамыту, білімге деген қызығушылықты қалыптастыру, сондай-ақ олардың ақыл-ой белсенділігін арттыру үшін алгебралық теңдеулерді үйренуге жағдай жасауды ұсынуға болады деп санаймыз.

Қолданылған әдебиеттер т

---

ізімі:

1. 
   Математика, информатика, физика журналы №5, 6, 2003ж.
   
2. 
   Брадис В.М. төрт таңбалы математикалық таблицалар – М.:Просвещение, 1990
   
3. 
   Ә.Н.Шыныбеков, Алгебра 8-сынып, Алматы «Атамұра» 2004
   
4. 
   Ш. Бекбаулиева, Қ.И. Қаңлыбаев, Н.Н. Забежанская, М.Б. Меңдіғалиева, Алматы «Ана тілі» 1991
   
5. 
   Математика журналы №4, 2007 ж.
   
6. 
   Алимов Ш.А., Ильин В.А. и др. Алгебра, 6-сынып.
   
7. 
   Алгебра: Учебник для 10-11 кл. ср. шк./Алимов Ш.А., Колягин Ю.М., Сидоров Ю.В. и др. М.: Просвещение, 1990.
   
8. 
   Богатырев Г.И., Боковнев О.А. Математика для подготовительных курсов техникумов на базе 8 классов средней школы. М.: Наука, 1988.
   
9. 
   Большой энциклопедический справочник. Математика. М: Большая российская энциклопедия, 1998.
   
10. 
    Болтянский В.Г., Сидоров Ю.В., Шабушин М.И. Лекции и задачи по элементарной математике. М.: Наука, 1972.
    
11. 
    Выгодский Н. Я. Справочник по элементарной математике. М.: Наука, 1979.
    
12. 
    Глейзер Г.И. История математики в школе. М.: Наука, 1981.
    
13. 
    Дорофеев Г.П., Потапов М.К. Пособие по математике для поступающих в ВУЗы. М.: Наука. гл. ред. физ.-мат. лит., 1976.
    

ҚАЗАҚСТАН РЕСПУБЛИКАСЫНЫҢ ҒЫЛЫМ ЖӘНЕ ЖОҒАРЫ БІЛІМ МИНИСТРЛІГІ

М.Өтемісов атындағы Батыс Қазақстан Университеті

Математика кафедрасы

КУРСТЫҚ ЖҰМЫС

Тақырыбы: Алгебралық теңдеулердің теориялық ерекшеліктері

Орындаған: ММ-21 тобы Шекербек А.Б

Тексерген: ф-м.ғ.к., Жумагалиева А.Е

Орал 2022 жыл

Курстық жұмыстың мақсаты:

Курстық жұмыстың міндеті:

Курстық жұмыстың құрылымы:

---

Смотрите также файлы

• Тема Прочитайте и переведите текст. Обратите внимание на выделенные слова и словосочетания это основные лексические единицы данной темы..doc

• азастан тарихы пнінен 7 сыныпты кнтізбеліктаырыпты жоспар жылына 72 с, аптасына 2 c.docx

• 1 Тапсырма Сратара жауап бер.docx

• Закон единства количественных и качественных изменений. Диалектика связи эволюции и революции в развитии.docx

• Методические рекомендации по написанию, оформлению и защите.pdf