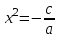Файл: 2 Алгебралы тедеулерді теориялы ерекшеліктері.docx

Скачать файл
Заказать решение

ВУЗ: Не указан

Категория: Не указан

Дисциплина: Не указана

Добавлен: 04.02.2024

Просмотров: 29

Скачиваний: 0

ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
бір-біріне тең.

Салдары. Кез-келген терминді теңдеудің бір бөлігінен екінші бөлігіне қарама-қарсы белгімен ауыстыруға болады.

Мысалы, .

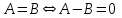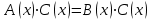2) теңдеуі теңдеуге тең , мұндағы С- теңдеудің рұқсат етілген мәндерінің жиынында мағынасы бар және нөлге айналмайтын сан немесе теңдеу.

Бұл қасиеттің дәлелі өрнектің 1 қасиетіне ұқсас.

Салдары. Теңдеудің екі бөлігін де рұқсат етілген мәндер жиынында нөлге айналмайтын ортақ факторға қысқартуға болады.

Шынында да 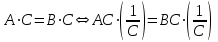теңдеуі, теңдеуге тең .

3) 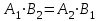теңдеу бастапқы 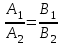теңдеудің рұқсат етілген мәндерінің жиынында 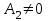немесе қосымша шартпен оның жиынында қарастырылған теңдеуге тең 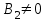. Бұл қасиеттер теңдеулерді шешуде қолданылады.

§2. Сызықтық теңдеулер.

Анықтама. Бір белгісізі бар бірінші дәрежелі теңдеу 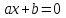көрсеткіш теңдеуі деп аталады,мұндағы берілген сандар 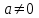және х белгісіз.

Бұл жағдайда 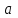саны х-тің белгісіз мәніндегі коэффициент деп аталады, ал b саны бос мүше

Бұл теңдеу 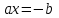біз алатын теңдеуге тең . Осылайша, бірінші дәрежелі теңдеудің әрқашан 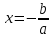бір түбірі болады .

Бірінші дәрежелі теңдеу 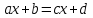сызықтық теңдеуінің ерекше жағдайы болып табылады, мұндағы 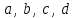- берілген сандар, ал
- белгісіз.

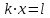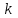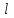Сызықтық теңдеу оған тең келетін түр теңдеуіне дейін азаяды, мұндағы және - белгілі сандар. Бұл жағдайда 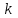сан-белгісіз коэффициент, бірінші дәрежелі теңдеудегі белгісіз коэффициентке қарағанда нөлге тең болуы мүмкін.

Сызықтық теңдеудің түбірі жоқ немесе шексіз түбір жиынтығы болуы мүмкін.

Мысал 1. 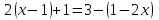теңдеуінің түбірі жоқ екенін көрсету.

Шешім. Бұл теңдеу 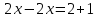теңдеуге тең, немесе .

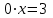Бұл теңдеудің еш түбірі жоқ, себебі теңдеудің 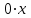сол жағы -тің кез-келген мәнінде нөлге тең, яғни 3 ке тең емес. [1, c.34]

Мысал 2. 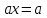теңдеуін шешу.

Шешім. Бұл теңдеуде параметр бар (берілген есепте бірдей мәнді сақтайтын айнымалы).

Егер болса, онда 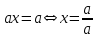яғни, теңдеудің жалғыз түбірі.

Егер 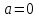теңдеу 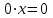форманы алса және оның түбірі кез-келген нақты сан болса .

Мысал 3. Теңдеуді шешіңіз



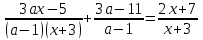
Шешімі.

1) Бөлшектерді 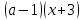жалпы бөлгішке келтіргеннен кейін , егер 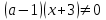, яғни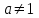 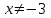, болса , бастапқы теңдеуге тең 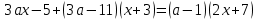сызықтық теңдеу аламыз .


2) осындай мүшелер келтірілгеннен кейін және алынған теңдеуді сызықтық теңдеу үшін стандартты 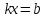түрге келтіргеннен кейін бізде ,(*)

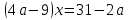3) а) егер 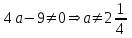болса, онда 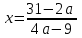. Енді табылған мән бастапқы теңдеудің анықтау өрісі бойынша мүмкін болмайтын параметр мәндерін алып тастау керек. 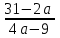бөлшекті 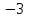теңестіреміз:

, , .

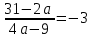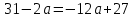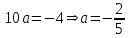Осылайша, түрлендіру нәтижесінде алынған сызықтық 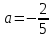теңдеудің бастапқы теңдеу үшін бөгде 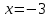түбірі болады.

б) егер 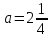, онда (*) теңдеу 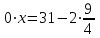түрді алады немесе 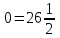- дұрыс емес теңдік, яғни (*)теңдеудің түбірі жоқ.

Жалпы, егер теңдеудің түбірлері болмаса, онда теңдеудің түбірлерінің жиынтығы бос деп айтылады және Ø деп белгіленеді.

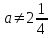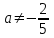Жауап. 1) , және теңдеудің жалғыз 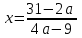шешімі бар ;

2) 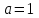кезінде бұл теңдеудің мағынасы жоқ;

3) 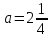және 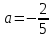кезінде шешімдері;

Жауабын қысқаша түрде жазуға болады:

  1. егер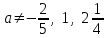 , онда ;

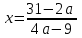2)егер 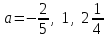, онда Ø.

§3. Квадрат теңдеулер. Виет теоремасы (тікелей және кері).

Анықтама. Квадрат теңдеу (немесе екінші дәрежелі теңдеу) 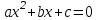түрдің теңдеуі деп аталады , мұндағы 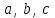берілген сандар және белгісіз. 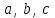сандар квадрат теңдеудің коэффициенттері деп аталады: - белгісіз квадраттағы коэффициент, 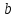- бірінші дәрежелі белгісіз коэффициент, 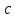- еркін термин.

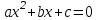квадрат теңдеу коэффициенттердің кем дегенде біреуі немесе 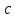нөлге тең болса, толық емес деп аталады.

Толық емес квадрат теңдеу-келесі түрлердің бірінің теңдеуі:







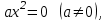
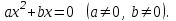
Толық емес квадраттық теңдеулердің қалай шешілетінін көрсетейік:

1. 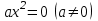теңдеуінің жалғыз шешімі бар.

2. 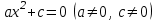теңдеуі 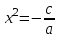теңдеуіне тең.

Екі жағдай болуы мүмкін.

Егер 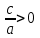, онда 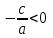, сондықтан 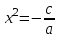теңдеудің нақты түбірі жоқ.

Егер 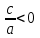, онда 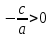және теңдеудің екі түбірі бар: , .

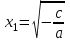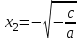
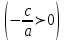Шынында да,

Смотрите также файлы