ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 20.03.2024
Просмотров: 246
Скачиваний: 0
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
· 20
Как теперь можно записать это число в двоичной системе счисления?
12=1*21+…. 75=1*26+… 150=1*27+… .513=1*29+….
Покажите ход ваших рассуждений:
В развернутой форме записи любое число можно записать как сумму произведений цифр на основание системы счисления в соответствующей номеру позиции степени. Так определили старшую степень в развернутой форме записи
«Для того чтобы перевести число, записанное в системе с основанием x, в десятичную систему, нужно
каждый разряд числа необходимо умножить на X n, где X - основание исходного числа, n - номер разряда. Затем суммировать полученные значения .
Ответ: x =
16x + 33x = 52x. Решение:
x>6 ; в 10-ой 16x=x+6; 33x=3*x+3; 52x=5*x+2; Уравнение 4*x+9=5*x+2 ; x=7
Ответ: x =
Как вычислить его значение?
Как вычислить его значение?
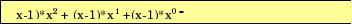
1203 =
= 
3215 =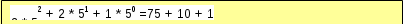
= 
110112 =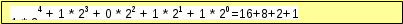
= 
1538 =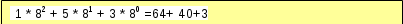
= 
12316 =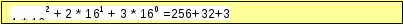
= 
= 
= 
= 
= 
=
= 
=
= 
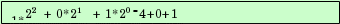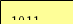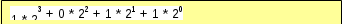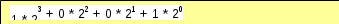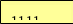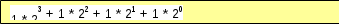«Последняя цифра двоичной записи числа – это
от его деления на 
».
16 =
24 = 
20 =
28 = 
Закончите фразы:
«Если число делится на 4, то его двоичная запись заканчивается на
».
«Если число делится на 8, то его двоичная запись заканчивается на
».
«Если число делится на 16, то его двоичная запись заканчивается на
».
101 =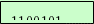
2 
нулей
48 =
2 
нулей
73 =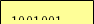
2 
нулей
88 =
2 
нулей
96 =
2 
нулей
111 =
2 
нулей
117 =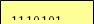
2
нулей
152 =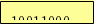
2 
нулей
254 =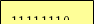
2 
нулей
Как теперь можно записать это число в двоичной системе счисления?
-
Для каждого из чисел определите старшую степень в развёрнутой форме через степени числа 2:
12=1*21+…. 75=1*26+… 150=1*27+… .513=1*29+….
Покажите ход ваших рассуждений:
В развернутой форме записи любое число можно записать как сумму произведений цифр на основание системы счисления в соответствующей номеру позиции степени. Так определили старшую степень в развернутой форме записи
-
Сформулируйте правила перевода числа из любой позиционной системы в десятичную:
«Для того чтобы перевести число, записанное в системе с основанием x, в десятичную систему, нужно
каждый разряд числа необходимо умножить на X n, где X - основание исходного числа, n - номер разряда. Затем суммировать полученные значения .
-
В некоторой системе счисления число 45 записывается как 63x. Определите основание x этой системы счисления. Решение:
Ответ: x =
-
Найдите основание x системы счисления, в которой выполняется равенство
16x + 33x = 52x. Решение:
x>6 ; в 10-ой 16x=x+6; 33x=3*x+3; 52x=5*x+2; Уравнение 4*x+9=5*x+2 ; x=7
Ответ: x =
-
Как записывается наименьшее трёхзначное число в системе счиcления с основанием x?
x .
Как вычислить его значение?
-
Как записывается наибольшее трёхзначное число в системе счиcления с основанием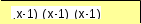 x?
x =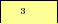 
x – 1.
Как вычислить его значение?
-
Запишите в развёрнутой форме числа и переведите их в десятичную систему счисления. Используйте образец.
1203 =
= 3215 =
= 110112 =
= 1538 =
= 12316 =
= - 1 2 3 4 5 6 7 8 9
Двоичная система счисления
-
Запишите над числами номера разрядов и переведите числа в десятичную систему счисления числа. Используйте образец.
= = = = = = = = -
Переведите числа в двоичную систему счисления, разложив число на сумму степеней числа 2. Используйте образец в первой строчке.
x
64
32
16
8
4
2
1
x2
26
25
24
23
22
21
20
13
1
1
1
11012
19
1
1
1
100112
25
1
1
1
110012
31
1
1
1
1
1
111112
38
1
1
1
1001102
45
1
1
1
1
1011012
56
1
1
1
1110002
73
1
1
1
10010012
88
1
1
1
10110002
108
1
1
1
1
11011002
120
1
1
1
1
11110002
-
С помощью какой математической операции можно найти последнюю цифру двоичной записи числа? Заполните пропуски:
«Последняя цифра двоичной записи числа – это
от его деления на ».-
Переведите в двоичную систему счисления числа:
16 =
24 = 20 =
28 = Закончите фразы:
«Если число делится на 4, то его двоичная запись заканчивается на
».«Если число делится на 8, то его двоичная запись заканчивается на
».«Если число делится на 16, то его двоичная запись заканчивается на
».-
Сколько значащих нулей в двоичной записи чисел
101 =
2 нулей 48 =
2 нулей 73 =
2 нулей 88 =
2 нулей 96 =
2 нулей 111 =
2 нулей 117 =
2
нулей 152 =
2 нулей 254 =
2 нулей - 1 2 3 4 5 6 7 8 9