Файл: Курсовая работа по дисциплине Подвижной состав железных дорог.docx
Добавлен: 10.04.2024
Просмотров: 141
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
СОДЕРЖАНИЕ
2.2. Обозначения и область применения габаритов
2.3. Определение горизонтальных поперечных размеров строительного очертания вагона
2.5. Определение размеров проектного очертания вагона
4.1. Вертикальные нагрузки, действующие на кузов и детали тележки
Статическая нагрузка на любую деталь вагона определяется по формуле:
4.1.2. Вертикальная динамическая нагрузка
4.1.3 Суммарная вертикальная нагрузка
4.1.2. Вертикальная динамическая нагрузка
Вертикальная динамическая нагрузка определяется умножением статической нагрузки на коэффициент вертикальной динамики, то есть:

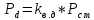
где
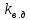 – коэффициент вертикальной динамики.
– коэффициент вертикальной динамики.Коэффициент вертикальной динамики определяется по формуле:
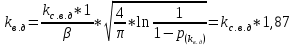
где
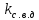 – среднее вероятное значение коэффициента вертикальной динамики;
– среднее вероятное значение коэффициента вертикальной динамики;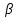 – параметр распределения (уточняется по экспериментальным данным), для грузовых вагонов при существующих условиях эксплуатации
– параметр распределения (уточняется по экспериментальным данным), для грузовых вагонов при существующих условиях эксплуатации 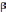 =1,13.
=1,13.При оценке прочности по допускаемым напряжениям, принятым согласно расчетным режимам, расчетная вероятность принимается как:
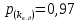
Среднее вероятное значение
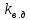 определяется по следующей формуле для скоростей движения вагона
определяется по следующей формуле для скоростей движения вагона 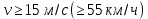 :
: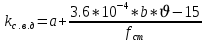
 где
где  — коэффициент, принимаемый на основании обработки результатов теоретических и экспериментальных исследований равный для элементов кузова вагона 0,05; для обрессоренных частей тележки 0,10; для необрессоренных частей тележки 0,15;
— коэффициент, принимаемый на основании обработки результатов теоретических и экспериментальных исследований равный для элементов кузова вагона 0,05; для обрессоренных частей тележки 0,10; для необрессоренных частей тележки 0,15;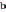 — коэффициент, учитывающий влияние числа осей в тележке (n), группе тележек под одним концом вагона на величину коэффициента динамики:
— коэффициент, учитывающий влияние числа осей в тележке (n), группе тележек под одним концом вагона на величину коэффициента динамики: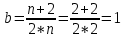
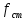 - статический прогиб рессорного подвешивания, 0,05м.
- статический прогиб рессорного подвешивания, 0,05м.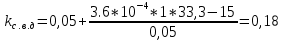
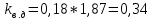
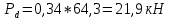
Вертикальные динамические нагрузки на обрессоренные части тележки:
а=0,1:
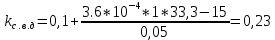
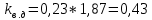
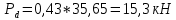
Вертикальные динамические нагрузки на необрессоренные части тележки:
а=0,15:
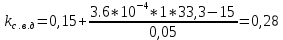
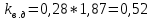
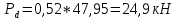
4.1.3 Суммарная вертикальная нагрузка
Эта нагрузка считается действующей статически на любую деталь тележки и складывается из вертикальной статической и вертикальной динамической нагрузок:
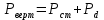
 На подпятник:
На подпятник: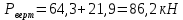
На рессорный комплект:
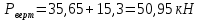
На боковую раму:
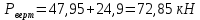
4.2. Боковые нагрузки
4.2.1. Боковая горизонтальная нагрузка
Боковая нагрузка, возникающая при движении вагона по кривому участку пути, складывается из центробежной силы и давления ветра на кузов и равна:
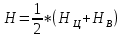
где
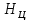 — центробежная сила, направленная наружу кривой, кН;
— центробежная сила, направленная наружу кривой, кН;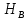 — равнодействующая сила давления ветра на кузов вагона, кН.
— равнодействующая сила давления ветра на кузов вагона, кН.Величина центробежной силы определяется с учетом возвышения наружного рельса над внутренним. В упрощенном виде:
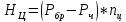
где
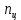
— коэффициент, определяемый по формуле
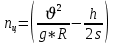
где
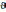 — скорость движения вагона, м/с;
— скорость движения вагона, м/с;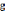 — ускорение свободного падения тел, м/с2
— ускорение свободного падения тел, м/с2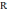 — радиус кривой, м;
— радиус кривой, м;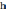 — возвышение наружного рельса над внутренним, мм;
— возвышение наружного рельса над внутренним, мм;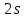 — расстояние между кругами катания колесной пары, мм.
— расстояние между кругами катания колесной пары, мм. Если в технических требованиях не оговорены особые условия движения в кривых, то
 =0,075 для грузовых вагонов.
=0,075 для грузовых вагонов.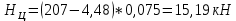
Равнодействующую силу давления ветра определяют по формуле:
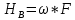
где
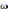 — удельное давление ветра, перпендикулярное боковой стене вагона, принимаемое согласно нормам расчета на прочность равным 500 Н/м2
— удельное давление ветра, перпендикулярное боковой стене вагона, принимаемое согласно нормам расчета на прочность равным 500 Н/м2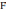 — площадь боковой проекции кузова, м2.
— площадь боковой проекции кузова, м2.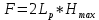
где
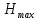 – максимальная высота кузова с учетом рамы вагона,
– максимальная высота кузова с учетом рамы вагона, 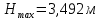
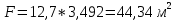
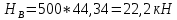
Боковая горизонтальная нагрузка:
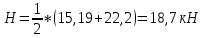
 4.2.2. Вертикальные составляющие боковых нагрузок
4.2.2. Вертикальные составляющие боковых нагрузок
Боковые нагрузки вызывают дополнительное вертикальное загружение частей тележек с одной стороны вагона и соответствующее разгружение с другой. Величина такого дополнительного загружения рассчитываемой детали находится по формуле:
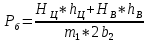
где
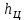 и
и 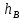 — вертикальные расстояния от места приложения
— вертикальные расстояния от места приложения 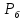 до точек приложения сил
до точек приложения сил  и
и 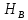 соответственно, м;
соответственно, м;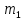 — число одноименных, параллельно нагруженных элементов, расположенных с одной стороны вагона;
— число одноименных, параллельно нагруженных элементов, расположенных с одной стороны вагона;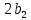 — расстояние между точками приложения сил
— расстояние между точками приложения сил 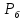 дополнительного загружения и разгружения рассчитываемой детали =2,06
дополнительного загружения и разгружения рассчитываемой детали =2,06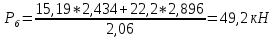
5. Устойчивость колесной пары против схода с рельсов
При движении по рельсовой колее, возможно, такое положение колесной пары, при котором одно из колес набегает гребнем на рельс. Плоскость круга катания колеса при этом составляет некоторый угол φн, называемый углом набегания. При этом колесо стремится взойти на рельс по плоскости скольжения, касательной наружной поверхности гребня и составляющей угол β с горизонтальной осью (угол наклона гребня).
 Вползание гребня на головку рельса предотвращается, если проекции всех вертикальных сил на плоскость скольжения больше проекции горизонтальных сил, причем считается, что эти силы приложены к точке контакта колеса и головки рельса. Устойчивость колеса против схода с рельса является одним из главных условий безопасности движения вагона.
Вползание гребня на головку рельса предотвращается, если проекции всех вертикальных сил на плоскость скольжения больше проекции горизонтальных сил, причем считается, что эти силы приложены к точке контакта колеса и головки рельса. Устойчивость колеса против схода с рельса является одним из главных условий безопасности движения вагона.
Согласно нормам для оценки устойчивости колеса против схода с рельсов подсчитывается коэффициент устойчивости кус и требуется соблюдение следующего условия:
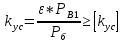
где [кус]= 1,5 – допускаемое значение коэффициента устойчивости для грузовых вагонов;
ε – коэффициент, определяемый по формуле:
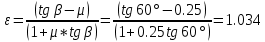
β – угол наклона образующей гребня колеса к горизонтальной оси, который у стандартного колеса равен 60º, у колеса, разработанного ВНИИЖТом, – 65º, у колеса, разработанного ОСЖД специально для отечественных железных дорог, – 70º (кроме перечисленных колес могут применяться и другие колеса со специальными профилями);
μ – коэффициент трения скольжения ненабегающего колеса о головку рельса, μ =0,25;
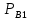 – вертикальная составляющая силы реакции набегающего колеса на головку рельса, тс;
– вертикальная составляющая силы реакции набегающего колеса на головку рельса, тс;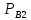 – вертикальная составляющая силы реакции ненабегающего колеса на головку рельса, тс;
– вертикальная составляющая силы реакции ненабегающего колеса на головку рельса, тс; – горизонтальная составляющая силы реакции набегающего колеса на головку рельса, действующая одновременно с Рв1 и Рв2,.
– горизонтальная составляющая силы реакции набегающего колеса на головку рельса, действующая одновременно с Рв1 и Рв2,.Усилия
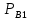 ,
, 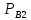 ,
,  определяются по формулам:
определяются по формулам: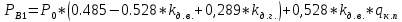
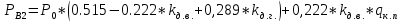
где
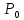 – осевая нагрузка, тс;
– осевая нагрузка, тс;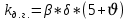 среднее значение коэффициента горизонтальной динамики колесной пары;
среднее значение коэффициента горизонтальной динамики колесной пары;где
 – коэффициент осности тележки;
– коэффициент осности тележки;
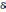 – коэффициент, зависящий от гибкости рессорного подвешивания, для грузовых вагонов б = 0,003;
– коэффициент, зависящий от гибкости рессорного подвешивания, для грузовых вагонов б = 0,003;

