Файл: Курсовая работа Теоретическая механика (семестр 4).docx

Уравнения (2.17) составляют систему алгебраических уравнений относительно функций , , , , , , , .

3. ПРИМЕНЕНИЕ ПРИНЦИПА ДАЛАМБЕРА-ЛАГРАНЖА И УРАВНЕНИЙ ЛАГРАНЖА 2 РОДА

3.1 Составление дифференциального уравнения движения механизма с помощью принципа Даламбера – Лагранжа

Общее уравнение динамики системы есть математическое выражение принципа Даламбера-Лагранжа

.

(3.1)

Здесь – сумма элементарных работ всех активных сил на возможном перемещении системы; – сумма элементарных работ всех сил инерции на возможном перемещении системы.

Изобразим на рисунке активные силы и силы инерции (рис. 4). Пружина является неидеальной связью. Введем реакцию этой связи в число активных сил.

Сообщим системе возможное перемещение. Составим кинематическое соотношение для системы:

Откуда
,



,

---

2. 
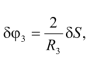
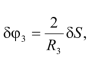
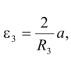
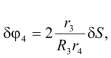
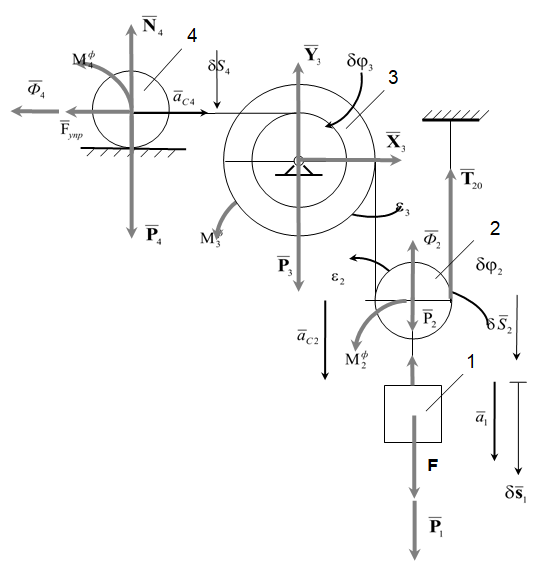
   Расчетная схема.
   

Работа активной силы определяется

, .
Работы некоторых внешних сил будут равняться нулю, т.к. они приложены в точках, скорости которых равны нулю. Как видно из расчетной схемы, таковыми являются силы . Возможная работа остальных активных сил определяется как сумма следующих элементарных работ:

,

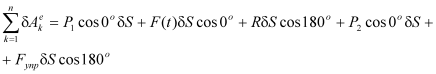(3.2)

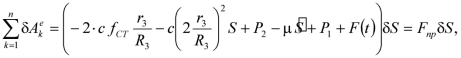
где 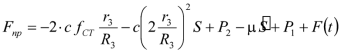. (3.3)
В состоянии покоя системы приведенная сила равна нулю. Полагая в (3.3) получаем условие равновесия системы

откуда определяется статическое удлинение пружины
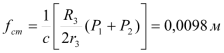. (3.4)

Учитывая (3.2) и (3.4), получаем окончательное выражение для приведенной силы
.
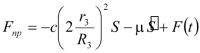Аналогичное выражение для приведенной силы было получено ранее (1.14).

Найдем возможную работу сил инерции:

(3.5)

Используя кинематические соотношения

---

, можно записать
,



,
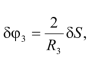
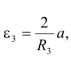
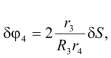
Тогда для величин главных векторов и главных моментов сил инерции имеем следующие выражения

	, , , , , .	(3.6)
или,	; , , , , .	(3.7)

Тогда возможную работу сил инерции можно преобразовать к виду

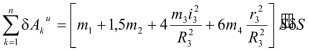(3.8)

или

,

(3.9)

---

где .

Аналогичное выражение для приведенной массы системы было получено ранее (1.8). Подставляя выражения (3.3) и (3.9) в общее уравнение динамики (3.1) получим

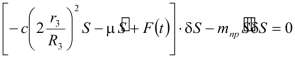(3.10)

Разделив (3.10) на , получаем дифференциальное уравнение вынужденных колебаний системы:

,

(3.11)

где , , .


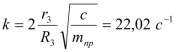Дифференциальное уравнение (3.11) полностью совпадает с уравнением (1.15) полученным ранее.

---

3.2 Составление дифференциального уравнения движения механизма с помощью уравнения Лагранжа 2 рода

Составим теперь уравнение Лагранжа 2-го рода. В качестве обобщенной координаты примем перемещение груза 1 – . Для механической системы с одной степенью свободы дифференциальное уравнение движения в обобщенных координатах имеет вид:

(3.12)

где – кинетическая энергия системы; – обобщенная сила; – обобщенная координата.

Составим кинематические соотношения системы:
,

, , .
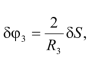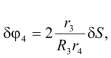
Вычислим кинетическую энергию системы как сумму кинетических энергий тел, образующих механическую систему.

Груз 1 совершает поступательное движение. Его кинетическая энергия равна:

.

(3.13)

Блок 2 и каток 4 совершают плоскопараллельное движение, поэтому

,

(3.14)

где , – моменты инерции блока 2 и катка 4.

Блок 3 совершает вращательное движение около неподвижной оси. Его кинетическая энергия определяется по формуле:

---