Файл: Курсовая работа Теоретическая механика (семестр 4).docx
Добавлен: 10.04.2024
Просмотров: 78
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
СОДЕРЖАНИЕ
«Теоретическая механика (семестр 4)»
Схема механизма и данные для выполнения задания
2. ОПРЕДЕЛЕНИЕ ЗАКОНА ДВИЖЕНИЯ СИСТЕМЫ И РЕАКЦИЙ ВНЕШНИХ И ВНУТРЕННИХ СВЯЗЕЙ.
2.1 Определение закона движения системы
2.2 Определение реакций внешних и внутренних связей
3. ПРИМЕНЕНИЕ ПРИНЦИПА ДАЛАМБЕРА-ЛАГРАНЖА И УРАВНЕНИЙ ЛАГРАНЖА 2 РОДА
3.2 Составление дифференциального уравнения движения механизма с помощью уравнения Лагранжа 2 рода
| | | (3.15) |
где
Кинетическая энергия всего механизма будет равна:
| | | (3.16) |
Так как система имеет одну степень свободы и в качестве координаты, определяющей ее положение, ранее принято перемещение груза 1, то кинематические характеристики всех тел механизма легко выражаются через кинематические параметры груза 1 соотношениями:
| | | (3.17) |
Подставляя (1.2), (1.3), (1.4) в (1.5) с учетом (1.6), окончательно получаем:
| | | | |
| где | | (3.18) | |
Учитывая, что
Производные от кинетической энергии
Для определения обобщенной силы сообщим системе возможное перемещение, при котором координата получит приращение , и вычислим сумму элементарных работ всех активных сил на возможном перемещении точек их приложения.
Работы некоторых внешних сил будут равняться нулю, т.к. они приложены в точках, скорости которых равны нулю. Как видно из расчетной схемы, таковыми являются силы
| | 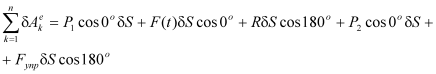 | (3.20) |
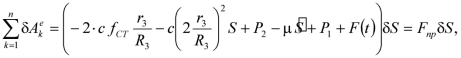
где
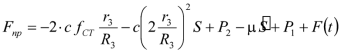 . (3.21)
. (3.21)В состоянии покоя системы приведенная сила равна нулю. Полагая в (3.21)
откуда определяется статическое удлинение пружины
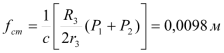 . (3.22)
. (3.22)Учитывая (3.20) и (3.22), получаем окончательное выражение для приведенной силы
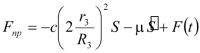 ,
,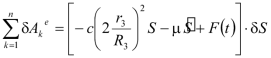 .
.В тоже время известно, что
| | | (3.23) |
Из (3.23) получаем выражение для обобщенной силы:
| | 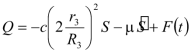 | (3.24) |
Подставляя кинетическую энергию (3.19) и обобщенную силу (3.24) в уравнениеЛагранжа получаем
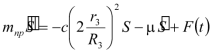
или
где
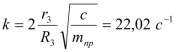 ,
, ,
Полученное уравнение (3.25) совпадает с уравнениями (1.15) и (3.11).
4. ПОСТРОЕНИЕ АЛГОРИТМА ВЫЧИСЛЕНИЙ
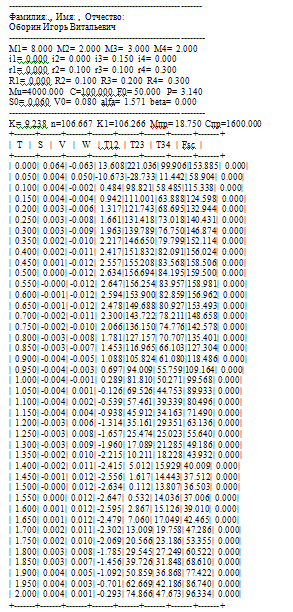
1. Исходные данные:
, , , , , , , , , , , , , , , .
2. Вычисление констант
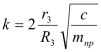 ,
,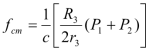 ,
,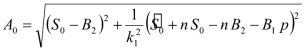 ,
,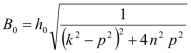 ,
,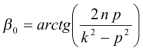 ,
,3. Задаем начальное время .
4. Вычисление искомых функций
5. Вычисление реакций связей
,
6. Определение значения времени на следующем шаге
7. Возврат к пункту 4. пока
8. Отображение результатов вычисления на графиках.
Результаты вычислений
Результаты оптимизации
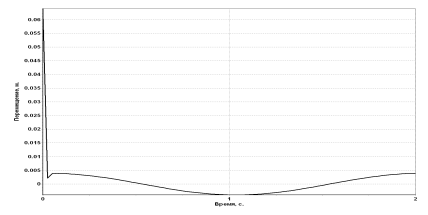
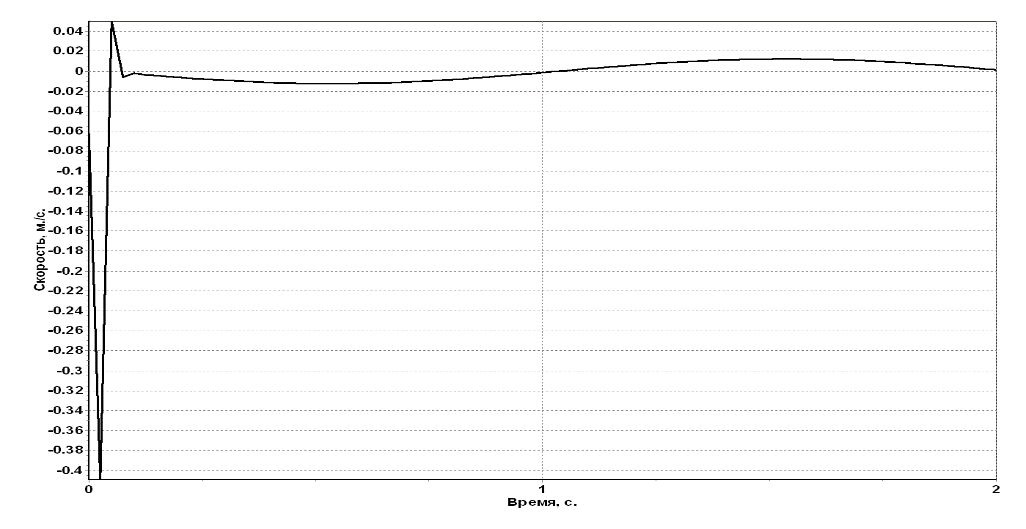
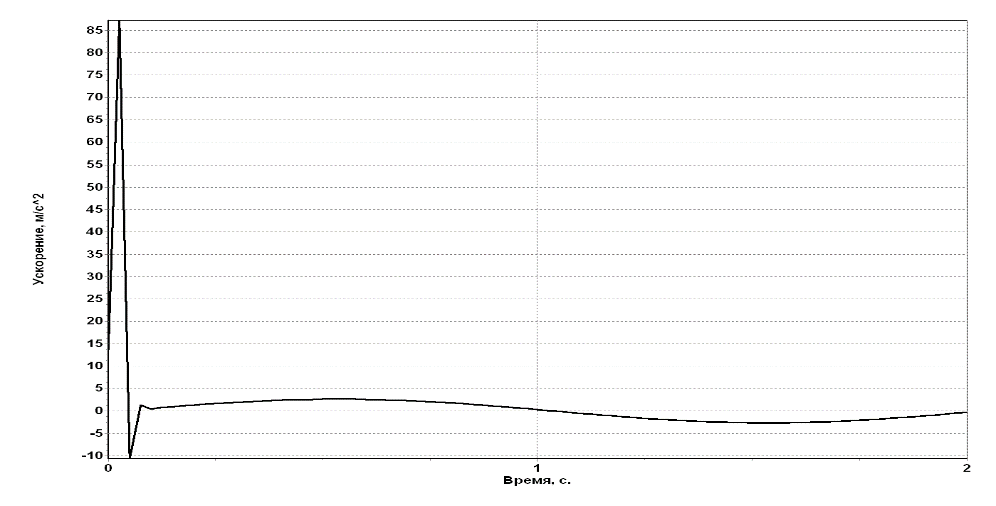
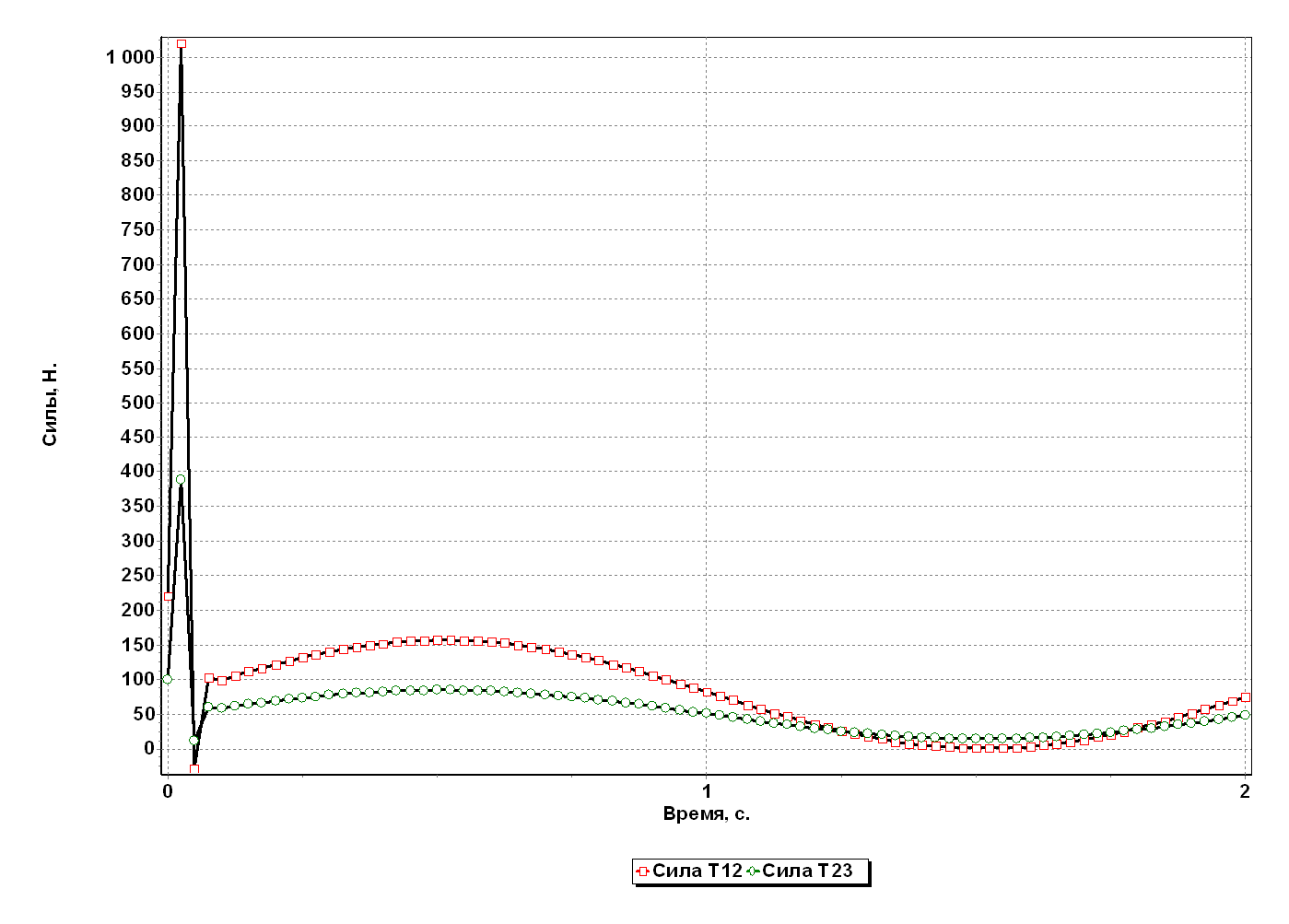
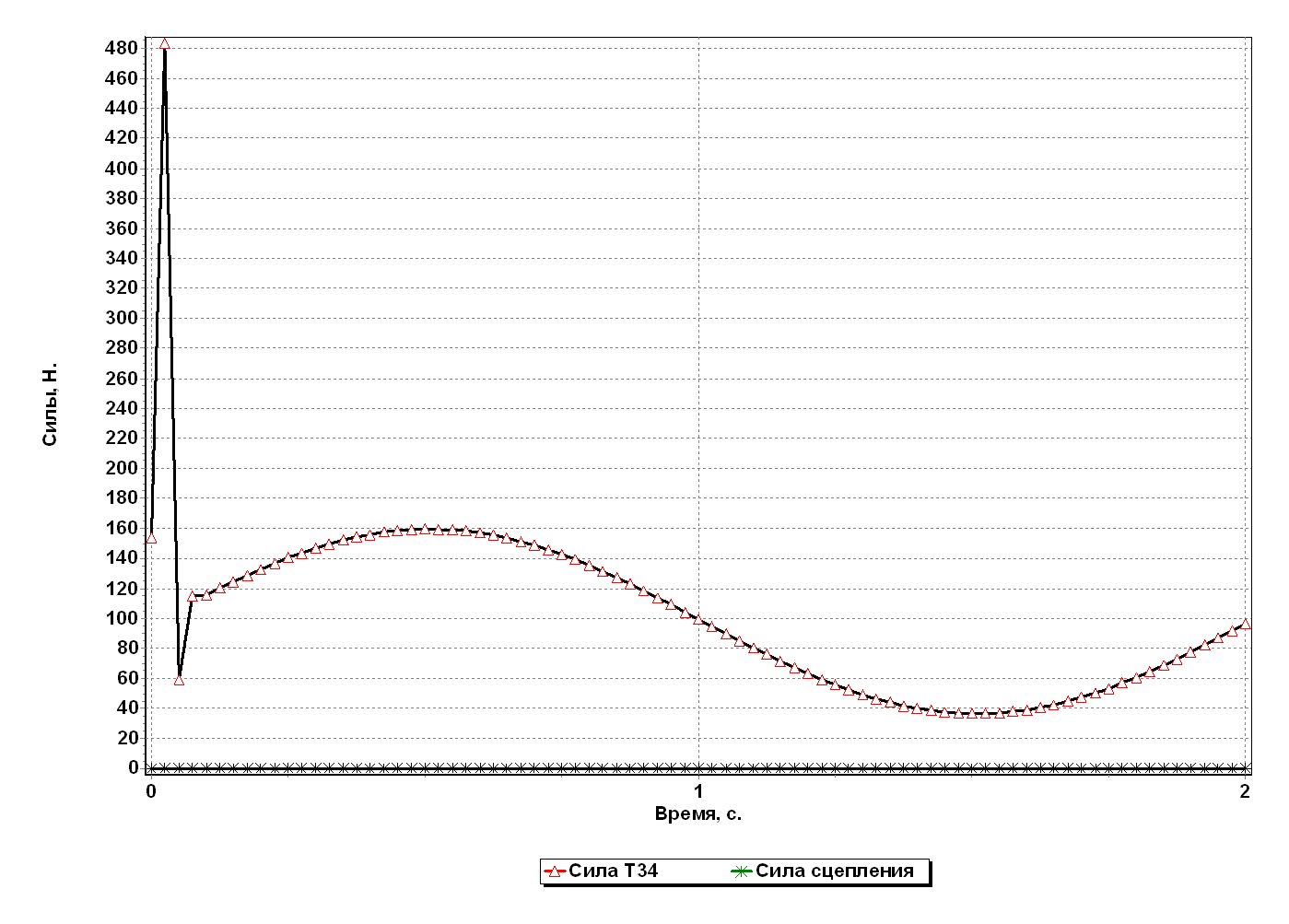
Анализ результатов оптимизации
Используя основные теоремы динамики системы и аналитические методы теоретической механики, мы определили закон движения первого тела и реакции внешних и внутренних связей. То, что при использовании различных теорем мы получили одинаковые законы движения, свидетельствует о правильности полученных результатов. Однако, из-за того, что исходные данные для расчета были выбраны произвольно, в некоторый момент наблюдалось провисание нитей, что привело бы к неверному описанию реального движения механизма полученным законом движения. Для приведения в соответствие реального закона движения с полученным на основе теорем, мы провели оптимизацию данных, в результате чего изменили массу первого тела с 2 до 8 кг.
Список использованной литературы
-
Методические указания для выполнения курсовой работы по разделу «Динамика» «Исследование колебаний механической системы с одной степенью свободы». -
Конспекты лекций по разделу «Динамика». -
Никитин Н.Н. Курс теоретической механики. - М.: Высшая школа, 1990. – 607 с. -
Яблонский А.А. Курс теоретической механики. Т.2. - М.: Высшая школа, 1984. - 424 с. -
Тарг С.М. Краткий курс теоретической механики. - М.: Наука, 1988. - 482 с.

