Файл: Курсовая работа Теоретическая механика (семестр 4).docx
Добавлен: 10.04.2024
Просмотров: 72
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
СОДЕРЖАНИЕ
«Теоретическая механика (семестр 4)»
Схема механизма и данные для выполнения задания
2. ОПРЕДЕЛЕНИЕ ЗАКОНА ДВИЖЕНИЯ СИСТЕМЫ И РЕАКЦИЙ ВНЕШНИХ И ВНУТРЕННИХ СВЯЗЕЙ.
2.1 Определение закона движения системы
2.2 Определение реакций внешних и внутренних связей
3. ПРИМЕНЕНИЕ ПРИНЦИПА ДАЛАМБЕРА-ЛАГРАНЖА И УРАВНЕНИЙ ЛАГРАНЖА 2 РОДА
3.2 Составление дифференциального уравнения движения механизма с помощью уравнения Лагранжа 2 рода
Министерство науки и высшего образования Российской Федерации Федеральное государственное бюджетное образовательное
учреждение высшего образования
«Тульский государственный университет»
Курсовая работа:
«Теоретическая механика (семестр 4)»
Вариант №8
Выполнил: Договор № ИИ01378
Чернявский Артем Николаевич
Проверила: канд. техн. наук, доц.
Ткач Ольга Александровна
Тула, 2022 г.
АННОТАЦИЯ
Исследуется движение механической системы с одной степенью свободы, представляющей собой совокупность абсолютно твердых тел, связанных друг с другом посредством невесомых нерастяжимых нитей, параллельных соответствующим плоскостям. Система снабжена внешней упругой связью с коэффициентом жесткости с. На первое тело системы действует сила сопротивления
движение тело нить механическая система
СОДЕРЖАНИЕ
«Теоретическая механика (семестр 4)» 1
Схема механизма и данные для выполнения задания 5
1. ВЫВОД ДИФФЕРЕНЦИАЛЬНОГО УРАВНЕНИЯ ДВИЖЕНИЯ С ИСПОЛЬЗОВАНИЕМ ТЕОРЕМЫ ОБ ИЗМЕНЕНИИ КИНЕТИЧЕСКОЙ ЭНЕРГИИ МЕХАНИЧЕСКОЙ СИСТЕМЫ 6
2. ОПРЕДЕЛЕНИЕ ЗАКОНА ДВИЖЕНИЯ СИСТЕМЫ И РЕАКЦИЙ ВНЕШНИХ И ВНУТРЕННИХ СВЯЗЕЙ. 12
2.1 Определение закона движения системы 12
2.2 Определение реакций внешних и внутренних связей 15
3. ПРИМЕНЕНИЕ ПРИНЦИПА ДАЛАМБЕРА-ЛАГРАНЖА И УРАВНЕНИЙ ЛАГРАНЖА 2 РОДА 18
3.1 Составление дифференциального уравнения движения механизма с помощью принципа Даламбера – Лагранжа 18
3.2 Составление дифференциального уравнения движения механизма с помощью уравнения Лагранжа 2 рода 23
4. ПОСТРОЕНИЕ АЛГОРИТМА ВЫЧИСЛЕНИЙ 28
Список использованной литературы 33
Схема механизма и данные для выполнения задания
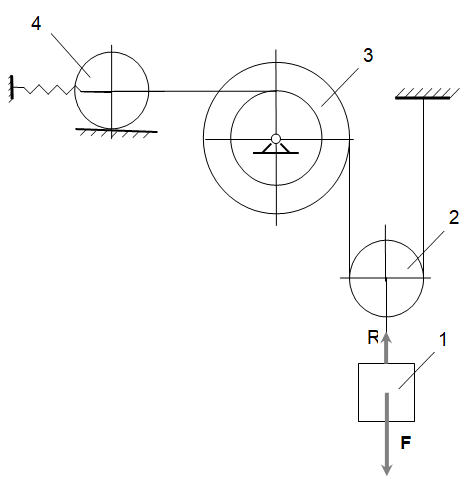
Рис 1. Схема механизма.
Дано:
| m1 = 2 кг | r2 = 0,1 м | c = 4000 Н/м | s0 = 0,06 м |
| m2 = 2 кг | r3 = 0,1 м | μ = 100 H⋅c/м | v0 = 0,08 м/с |
| m3 = 3 кг | R3 = 0,2 м | F0 = 50 Н | |
| m4 = 2 кг | i3 = 0,15 м | p = π = 3,14 с-1 | |
| | R4 = 0,3 м | | |
1. ВЫВОД ДИФФЕРЕНЦИАЛЬНОГО УРАВНЕНИЯ ДВИЖЕНИЯ С ИСПОЛЬЗОВАНИЕМ ТЕОРЕМЫ ОБ ИЗМЕНЕНИИ КИНЕТИЧЕСКОЙ ЭНЕРГИИ МЕХАНИЧЕСКОЙ СИСТЕМЫ
На рис. обозначено:
–нормальная реакция опорной плоскости,
– упругая реакция пружины,
Рассматриваемая механическая система имеет одну степень свободы. Будем определять положение системы с помощью координаты . Начало отсчета координат совместим с положением статического равновесия груза 1.
Для построения дифференциального уравнения движения системы используем теорему об изменении кинетической энергии механической системы в форме:
| | | (1.1) |
где обозначено:
Т – кинетическая энергия системы,
– сумма мощностей внешних сил,
– сумма мощностей внутренних сил.
Вычислим кинетическую энергию системы как сумму кинетических энергий тел, образующих механическую систему.
Вычислим кинетическую энергию системы как сумму кинетических энергий тел, образующих механическую систему.
Груз 1 совершает поступательное движение. Его кинетическая энергия равна:
| | | (1.2) |
Блок 2 и каток 4 совершают плоскопараллельное движение, поэтому
| | | (1.3) |
где
Блок 3 совершает вращательное движение около неподвижной оси. Его кинетическая энергия определяется по формуле:
| | | (1.4) |
где
Кинетическая энергия всего механизма будет равна:
| | | (1.5) |
Так как система имеет одну степень свободы и в качестве координаты, определяющей ее положение, ранее принято перемещение груза 1, то кинематические характеристики всех тел механизма легко выражаются через кинематические параметры груза 1 соотношениями:
| | | (1.6) |
Подставляя (1.2), (1.3), (1.4) в (1.5) с учетом (1.6), окончательно получаем:
| | | (1.7) | |
| где | | (1.8) | |
называется приведенной массой.
Теперь вычислим правую часть уравнения (1.1) – сумму мощностей внешних и внутренних сил.
Мощность силы равна скалярному произведению вектора силы на скорость точки приложения силы, а мощность момента силы – алгебраическому произведению момента силы на угловую скорость вращения тела, к которому приложен момент:
Знак "+" берется в том случае, если направления момента и угловой скорости одинаковы, а знак "–" если их направления противоположны.
Рассматриваемая нами механическая система является неизменяемой, т.е. тела, входящие в систему, не деформируемы и скорости их точек относительно друг друга равны нулю. Поэтому мощности внутренних сил будут равняться нулю
Будут равняться нулю и мощности некоторых внешних сил, приложенных в точках, скорости которых равны нулю. Как видно из расчетной схемы, таковыми являются силы
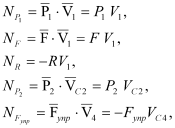
или
С учетом кинематических соотношений (1.6) сумму мощностей внешних сил преобразуем к виду:
| | | (1.9) |
| | | (1.10) |
называется приведенной силой.
Упругую силу считаем пропорциональной удлинению пружины. Полное удлинение пружины равно сумме статического и динамического удлинений
Тогда упругая сила будет равна:
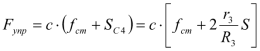 .
.Сила вязкого сопротивления
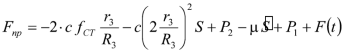 | (1.11) |
В состоянии покоя
| | | (1.12) |
Из уравнения (1.12) определяется статическое удлинение пружины
| | 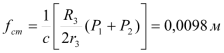 . . | (1.13) |
Таким образом, окончательное выражение для приведенной силы (1.11) будет иметь вид:
| | 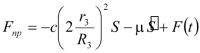 . . | (1.14) |
Подставим выражения для кинетической энергии (1.7) и сумму мощностей всех сил (1.9) с учетом (1.14) в уравнение (1.1). Тогда, после дифференцирования, получаем дифференциальное уравнение движения системы:
| | 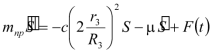 . . | |
Общепринято такие уравнения представлять в виде:


