Файл: Контрольные вопросы для самопроверки. Пособие содержит методические указания по теории погрешностей. Работы расположены в последовательности изложения материала курса Общая физика, раздел Механика.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 11.04.2024
Просмотров: 157
Скачиваний: 0
СОДЕРЖАНИЕ
ЧАСТЬ I. ЛАБОРАТОРНЫЕ РАБОТЫНАТУРНОГО ФИЗИЧЕСКОГО ЭКСПЕРИМЕНТА
Лабораторная работа № 1ОПРЕДЕЛЕНИЕ ЛИНЕЙНЫХ ВЕЛИЧИН И ПЛОТНОСТИ ТЕЛА
Лабораторная работа №2ПРОВЕРКА ОСНОВНОГО ЗАКОНА ДИНАМИКИПОСТУПАТЕЛЬНОГО ДВИЖЕНИЯ
Лабораторная работа №3ОПРЕДЕЛЕНИЕ КОЭФФИЦИЕНТА ТРЕНИЯ ПОКОЯ.
Лабораторная работа №4ОПРЕДЕЛЕНИЕ КОЭФФИЦИЕНТА ТРЕНИЯ СКОЛЬЖЕНИЯ
Лабораторная работа №5ОПРЕДЕЛЕНИЕ УСКОРЕНИЯ СВОБОДНОГО ПАДЕНИЯС ПОМОЩЬЮ МАШИНЫ АТВУДА
Лабораторная работа №6ИЗМЕРЕНИЕ СКОРОСТИ ПУЛИ С ПОМОЩЬЮБАЛЛИСТИЧЕСКОГО МАЯТНИКА
Лабораторная работа №7УПРУГОЕ СОУДАРЕНИЕ ШАРОВ
Лабораторная работа №8НЕУПРУГОЕ СОУДАРЕНИЕ ШАРОВ
Лабораторная работа №9ОПРЕДЕЛЕНИЕ МОМЕНТА ИНЕРЦИИ МАЯТНИКА ОБЕРБЕКА
Лабораторная работа №10ОПРЕДЕЛЕНИЕ МОМЕНТА ИНЕРЦИИ ТЕЛА ЭНЕРГЕТИЧЕСКИМ МЕТОДОМ
Лабораторная работа №11СКАТЫВАНИЕ ТВЕРДОГО ТЕЛА С НАКЛОННОЙ ПЛОСКОСТИ
Лабораторная работа №12МАТЕМАТИЧЕСКИЙ МАЯТНИК
Лабораторная работа №13ФИЗИЧЕСКИЙ МАЯТНИК
ЧАСТЬ II. ПОДСЧЕТ ПОГРЕШНОСТЕЙ ИЗМЕРЕНИЙ
Погрешность однократного прямого измерения
Учет случайной ошибки нескольких измеренийи ошибки однократного измерения
Алгоритм вычисления ошибки прямых равноточных измерений
МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ
Государственное образовательное учреждение высшего профессионального образования
«НАЦИОНАЛЬНЫЙ ИССЛЕДОВАТЕЛЬСКИЙ
ТОМСКИЙ ПОЛИТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ»
А.Н. Антоненко, А.В. Маркидонов
ЛАБОРАТОРНЫЙ ПРАКТИКУМ
МЕХАНИКА
Рекомендовано в качестве учебного пособия
Редакционно-издательским советом
Томского политехнического университета
Издательство
Томского политехнического университета
2011
УДК 000000
ББК 00000
C00
Антоненко А.Н.
Лабораторный практикум. Механика: учебное пособие / А.Н. Антоненко, А.В. Маркидонов; Томский политехнический университет. − Томск: Изд-во Томского политехнического университета, 2011. – 92 с.
Пособие содержит методические указания к лабораторным работам натурного физического эксперимента. Каждое указание имеет теоретическую часть, методические рекомендации к выполнению лабораторной работы, обработки результатов и контрольные вопросы для самопроверки. Пособие содержит методические указания по теории погрешностей. Работы расположены в последовательности изложения материала курса «Общая физика», раздел «Механика».
Предназначено для студентов и бакалавров технического университета.
УДК 000000
ББК 00000
Рецензенты
Доктор технических наук, профессор СибГиу
А.С. Никитин
Кандидат физико-математических наук, доцент КузГПА
П.П. Житников
Кандидат физико-математических наук, доцент НФ ТПУ
А.И. Антоненко
© ГОУ ВПО НИ ТПУ, 2011
© Антоненко А.Н., Маркидонов А.В., 2011
© Оформление. Издательство Томского
политехнического университета, 2011
ПРЕДИСЛОВИЕ
Данное пособие - результат коллективного труда преподавателей кафедры естественнонаучный и общепрофессиональных дисциплин Новокузнецкого филиала Томского политехнического университета.
Пособие является составной частью комплекса методического обеспечения учебного процесса по курсу «Общая физика», раздел Механика.
Пособие содержит методические указания к лабораторным работам натурного физического эксперимента (Часть 1). Каждое указание имеет теоретическую часть, методические рекомендации к выполнению лабораторной работы, обработки результатов и контрольные вопросы для самопроверки. Пособие содержит методические указания по теории погрешностей (Часть 2).
Лабораторные работы, представленные в пособии, охватывают почти все темы раздела «Механика». Работы расположены в последовательности изложения материала курса «Общей физики», раздел «Механика».
ВВЕДЕНИЕ
Одним из направлений подготовки бакалавров является формирование готовности к научно-исследовательской деятельности. Данное направление позволяет более эффективно готовить бакалавров к поступлению в магистратуру, в которой НИР становиться неотъемлемой частью учебного процесса.
Большие возможности в контексте формирования исследовательских навыков у студентов на первом курсе предоставляет изучение физики. В свою очередь, одной из самых активных форм изучения физики является выполнение лабораторных работ исследовательского и экспериментального характера. Она позволяет студентам не только наблюдать физические явления в различных условиях, выявлять их закономерности, знакомиться с техническими средствами и методами измерения физических величин, но и решать ряд исследовательских задач. Можно органически связать лекционный курс с лабораторным практикумом, так подобрать лабораторные работы, чтобы их выполнение помогало сформировать знания и умения для самостоятельной экспериментально-исследовательской деятельности.
Экспериментальные исследования тех или иных явлений представлены в пособии большим спектром лабораторных работ натурного эксперимента. Пособие содержит традиционные лабораторные работы, переработанные и модернизированные авторами. В каждую работу включены элементы проблемности разного плана: проблемные вопросы; задания на вывод формул, не содержащихся в теоретической части
; разработка альтернативной методики эксперимента или модификация данной работы.
Измерения физических величин производятся с ограниченной точностью. Ограничение точности ставит предел степени подробности информации, получаемой из эксперимента. Только в пределах точности измерений можно сравнивать результаты разных опытов друг с другом и с соответствующими предсказаниями теории.
Методики обработки информации и оценки точности измерений весьма разнообразны. Умения и навыки обработки информации об объекте одна из основных задач экспериментально-исследовательской деятельности в целом и учебного лабораторного практикума в частности.
В пособии содержатся подробные методические указания по подсчету погрешностей измерений. В лабораторной работе № 1 особое внимание уделено выводу формул для подсчета погрешностей косвенного измерения. Именно этот вопрос в теории и методики погрешностей измерений вызывает наибольшие затруднения у студентов первого курса.
ЧАСТЬ I. ЛАБОРАТОРНЫЕ РАБОТЫ
НАТУРНОГО ФИЗИЧЕСКОГО ЭКСПЕРИМЕНТА
Лабораторная работа № 1
ОПРЕДЕЛЕНИЕ ЛИНЕЙНЫХ ВЕЛИЧИН И ПЛОТНОСТИ ТЕЛА
Цель работы: Измерить линейные размеры тел с помощью приборов имеющих линейный нониус. Определить плотность тела. Ознакомится с методом расчета погрешностей.
Приборы и принадлежности: штангенциркуль, микрометр, весы, набор проволок различного диаметра, набор металлических трубок.
Краткое теоретическое введение
Техника непосредственного измерения длин достигла к настоящему времени большого совершенства. Сконструирован ряд специальных приборов, так называемых компараторов, позволяющих измерять длину с точностью до 1 микрометра (1 мкм=10-6м). Большинство этих приборов основано на применении микроскопа и некоторых других оптических приспособлений. При этом почти всегда отсчетные приспособления снабжены нониусами и микрометрами. Нониусом (линейным или круговым) называется специальная шкала, дополняющая обычный масштаб и позволяющая повысить точность измерений. Среди приборов, снабженных линейным нониусом, используемых в научных и учебных лабораториях, в цехах заводов и мастерских, следует отметить штангенциркуль, применяемый для измерения размеров технических деталей. Приборы с линейным нониусом позволяют проводить измерения с точностью 0.1 – 0.01 мм.
Линейный нониус представляет собой небольшую линейку с делениями, скользящую вдоль масштабной линейки и служащую для отсчета долей наименьшего деления масштаба.
Нониусы обычно изготовляются обычно таким образом, чтобы суммарная длина всех m делений нониуса была равна (m-1) наименьшим делением масштабной линейки. Если совместить нулевые метки нониуса и масштабной линейки (рис.1), то последняя m –я метка нониуса совпадает с (m–1) меткой масштаба (рис. 1).
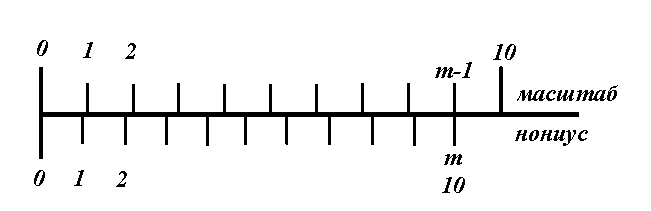
рис. 1
На рис.1 число всех делений нониуса m=10. Общая длина их соответствует длине 9 делений масштаба. Следовательно, если l – длина одного деления нониуса (цена деления нониуса), а y – длина наименьшего деления масштабной линейки (цена деления масштаба), то
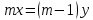 (1)
(1)Из (1) следует:
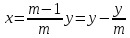
Отсюда можно найти разность длин делений шкалы и нониуса ∆x, которая называется точностью нониуса
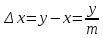 (2)
(2)При достаточно мелких делениях масштаба длина m делений нониуса может быть равна длине (km-1) делений масштаба, где k – целое число (k=2, 3…)
В этом случае
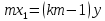
Отсюда
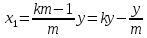
Точность этого нониуса будет выражаться по – прежнему формулой (2)
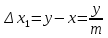
В любом положении нониуса относительно масштабной линейки одно из его делений или совпадет с каким–либо делением масштаба или ближе всего подходит к нему.
Отсчет по нониусу основан именно на способности глаза фиксировать это совпадение делений нониуса и масштаба.
Измерение длины L какого–либо предмета при помощи масштабной линейки с нониусом производится следующим образом: один конец предмета надо совместить с нулевым делением основной шкалы. Второй конец предмета при этом или совместится с некоторым k делением или окажется между k и (k+1) делениями масштаба (рис. 2)
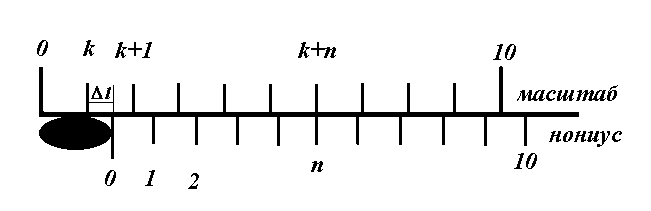
рис. 2
Следовательно, длину предмета в последнем случае можно выразить так:
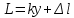 ,
, где ∆l - неизвестная величина, меньше одного деления масштаба, которую находят с помощью нониуса. Для этого к концу измеряемого предмета вплотную придвигается нониус. Так как деления нониуса не равны делениям масштаба, то обязательно найдется на нем такое деление n, которое совпадает или ближе всего подходит к соответствующему (k+n) делению масштаба (рис. 2)
Из рис.2 видно, что
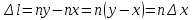
Значит длина измеряемого предмета будет:
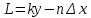
Или согласно выражению (2)
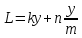 , (3)
, (3)
