Файл: Контрольные вопросы для самопроверки. Пособие содержит методические указания по теории погрешностей. Работы расположены в последовательности изложения материала курса Общая физика, раздел Механика.docx

рис. 2

Если грузы смещать относительно произвольно выбранной точки А на одинаковые расстояния r, то положение центра масс l (точка С) относительно точки О остается неизменным. При этом момент инерции Iтакого маятника будет меняться по закону:

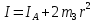, (5)

где 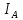– момент инерции маятника, при положении грузов m₃ в точке А.

Подставим выражение (8) в (7), и возведем в квадрат

(6)

где 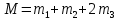– масса маятника.

Из этого выражения видно, что график функции 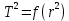представляет собой функцию типа 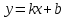(рис.2б).

Для нахождения момента инерции 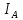необходимо полученный график экстраполировать до пересечения с осью r² и по точке пересечения К найти значение 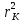. В этом случае , а следовательно выражение можно представить в виде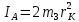

(7)

Для нахождения расстояния от оси вращения до центра масс l необходимо найти значение , соответствующее на графике точке N: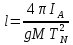

(8)

Пользуясь выражением (7) можно экспериментально найти значения момента инерции рассмотренного физического маятника

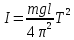(9)

Переведите секундомер в режим №4. Выведете маятник из положения равновесия на небольшой угол 5 - 10°. Отпустите груз и нажмите кнопку «Пуск» секундомера. Отсчитайте время t_изм равное 10 колебаниям и нажмите кнопку «Стоп/Сброс» секундомера. Период колебаний можно рассчитать по формуле

---

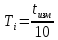
Порядок выполнения работы

1. 
   Установите симметрично грузы относительно точки А (рекомендуемое значение расстояния от оси вращения указано в таблице с исходными данными) на минимальное расстояние r.
   
2. 
   Измерьте время 10 колебаний и вычислите период колебаний T.
   
3. 
   Увеличивая расстояние r, измерьте соответствующие периоды колебаний. Проведите 5 измерений. Данные занесите в таблицу.
   

Таблица

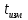№		Ti		ri		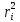I (теор.)	I (эксп.)
1
2
3
4
5

4. 
   Постройте график зависимости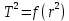 . Убедитесь, что полученный график представляет собой линейную функцию.
   
5. 
   Экстраполируйте полученный график до пересечения с осью r². По графику найдите точки пересечения с осями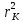 и .
   
6. 
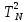   С помощью выражений (7) и (8) найдите значения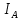 и l. Сравните полученное значение l с указанным в паспорте прибора расстоянием от оси вращения до центра тяжести маятника.
   
7. 
   Используя формулу (5), постройте теоретическую зависимость .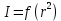
   
8. 
   В тех же осях, используя формулу (9), постройте практическую зависимость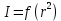 . Сравните полученные результаты.
   
9. 
   Сделайте выводы.
   

---

Контрольные вопросы

1. 
   Что такое физический маятник?
   
2. 
   Чему равен период колебаний физического маятника?
   
3. 
   Выведите уравнение колебаний физического маятника. Получите его решение.
   
4. 
   Как определяется момент инерции физического маятника в работе?
   
5. 
   Выведите формулу (9).
   
6. 
   Используя теорему Штейнера выведите формулу для момента инерции физического маятника использовавшегося в работе.
   
7. 
   Совпадают ли теоретически и практически полученные графики?
   
8. 
   *Предложите методику эксперимента, в котором бы учитывалось затухание колебаний, и имелась возможность расчета декремента затуханий колебаний.
   

---

ЧАСТЬ II. ПОДСЧЕТ ПОГРЕШНОСТЕЙ ИЗМЕРЕНИЙ

Виды измерений

Свойства физических объектов или процессов, которые можно прямо или косвенно измерить, называются физическими величинами.

Измерить какую-либо физическую величину значит сравнить ее с другой однородной ей физической величиной, принятой за единицу меры.

Виды измерений определяются физическим характером измеряемой величины, требуемой точностью измерения, необходимой скоростью измерения, условиями и режимом измерений и т. д.

По количеству проводимых опытов измерения можно разделить на многократные, однократные, необходимые, достаточные и т. д.

Наиболее часто используются прямые измерения, состоящие в том, что искомое значение величины находят из опытных данных путем экспериментального сравнения. Например, длину измеряют непосредственно линейкой, температуру - термометром, силу - динамометром и т. д.

Если искомое значение величины находят на основании известной зависимости между этой величиной и величинами, найденными прямыми измерениями, то этот вид измерений называют косвенными. Например, объем параллелепипеда находят путем умножения трех линейных величин (длины, ширины и высоты).

Совокупные измерения осуществляются путем одновременного измерения нескольких одноименных величин, при которых искомое значение находят решением системы уравнений, получаемых в результате прямых измерений и различных сочетаний этих величин.

Совместными называют производимые одновременно (прямые и косвенные) измерения двух или нескольких неодноименных величин. Целью этих измерений, по существу, является нахождение функциональной связи между величинами.

Проводимые при выполнении лабораторных работ измерения можно характеризовать как исследовательские, с точным или приближенным оцениванием погрешности, многократные или однократные, достаточные. Кроме того, измерения в лабораторных работах абсолютные, равноточные, прямые или косвенные, с использованием различных методов измерений.

Погрешности измерений

Как указывалось ранее, измерения проводят, чтобы получить численные значения нужной физической величины или установить функциональную зависимость. При прямых измерениях численные значения получаются непосредственно, а при косвенных измерениях вначале определяют одну или несколько исходных физических величин, а затем по их значениям вычисляют нужную физическую величину.

---

Опыт показывает, что вследствие неточности измерительных приборов, несовершенства наших органов чувств, неполноты наших знаний, трудности учета всех побочных явлений, при многократном повторении одного и того же измерения получаются разные численные значения. Так бывает, даже если измерения производить совершенно одинаково (равноточные измерения). При практическом использовании результатов тех или иных измерений возникает вопрос об истинном значении изучаемой физической величины, о точности измерения.

Термин «точность измерения», т. е. степень приближения результатов измерения к некоторому действительному значению используется для качественного сравнения измерительных операций. Для количественной оценки используется понятие «погрешность (ошибка) измерений» (чем меньше погрешность, тем выше точность). Оценка погрешности измерений - одно из важных мероприятий по обеспечению единства измерений.

Количество факторов, влияющих на точность измерений, достаточно велико, и любая классификация погрешностей измерений в известной мере условна.

Поэтому для практических целей достаточно рассмотреть случайные и систематические составляющие общей погрешности, выраженные в абсолютных и относительных единицах при прямых, косвенных, совокупных и равноточных измерениях.

Обозначим через х результат измерения некоторой величины, а через 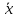— истинное значение ее, которое всегда нам неизвестно.

Тогда 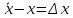представит погрешность измерения. Погрешность измерения — это отклонение результата измерений х от истинного 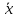(действительного) значения измеряемой величины.

В зависимости от формы выражения различают абсолютную, относительную и приведенную погрешности измерений.

Абсолютная погрешностьизмерения определяется как разность 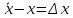. Абсолютная погрешность может быть положительной или отрицательной в зависимости от того уменьшен или увеличен результат измерения по отношению к истинному значению. Абсолютная, погрешность показывает величину интервала значений, в котором может находиться измеряемая величина. Абсолютная погрешность является размерной величиной.

---