Файл: Приближенные методы решения задач теории упругого режима фильтрации.docx
Добавлен: 17.10.2024
Просмотров: 27
Скачиваний: 0
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
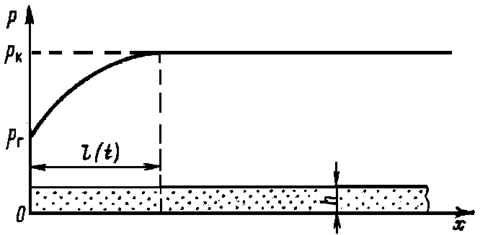
Рисунок 3 – Кривая распределения давления в прямолинейно-параллельном потоке по методу А. М. Пирвердяна
Рассмотрим прямолинейно-параллельный фильтрационный поток упругой жидкости (рисунок 3). В горизонтальном пласте постоянной толщины h и ширины B пущена в эксплуатацию галерея с постоянным дебитом Q. К моменту времени t после пуска граница возмущенной области продвигается на величину
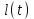 , при этом кривая распределения давления в этой области задается в виде параболы так, что в точке
, при этом кривая распределения давления в этой области задается в виде параболы так, что в точке 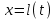 касательная к параболе горизонтальна, т.е.
касательная к параболе горизонтальна, т.е. 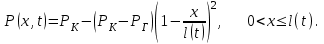 (1.3.1)
(1.3.1)Дебит галереи определяется по закону Дарси:
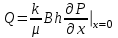 . (1.3.2)
. (1.3.2)Учитывая (1.3.1), находим выражение для дебита галереи:
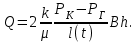 (1.3.3)
(1.3.3)Закон движения внешней границы возмущенной области определяется из уравнения материального баланса (как и при методе ПССС) и имеет вид:
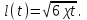 (1.3.4)
(1.3.4)Распределение давления (1.3.1) в возмущенной области пласта с учетом (1.3.3) и (1.3.4) принимает вид:
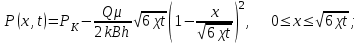
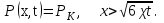 (1.3.5)
(1.3.5)Расчет депрессии
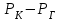 по формуле (1.3.5) дает погрешность по сравнению с точным решением примерно 9%, т.е. в 2,5 раза меньше, чем метод ПССС.
по формуле (1.3.5) дает погрешность по сравнению с точным решением примерно 9%, т.е. в 2,5 раза меньше, чем метод ПССС.Аналогичным образом строится решение и для случая плоскорадиального потока. В этом случае распределение давления в возмущенной области пласта задается в виде:
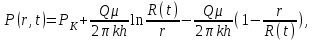 (1.3.6)
(1.3.6)где R(t) – радиус внешней границы возмущенной области пласта.
Заметим, что отбросив последнее слагаемое в уравнении (1.3.6), получаем закон распределения давления при методе ПССС [1].
1.4 Метод интегральных соотношений
Метод интегральных соотношений, предложенный Г.И. Баренблаттом, по аналогии с методами пограничного слоя в потоке вязкой жидкости позволяет получить приближенные решения некоторых задач нестационарной фильтрации упругой жидкости с нужной точностью. Метод основан на следующих предпосылках:
1. В каждый момент времени пласт делится на конечную возмущенную область и невозмущенную область, где движение отсутствует.
2. В возмущенной области распределение давления представляется в виде многочлена по степеням координаты х или r (в случае радиального потока добавляется еще логарифмический член) с коэффициентами, зависящими от времени, так что:
для прямолинейно-параллельного потока:
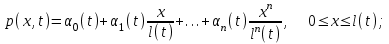 (1.4.1)
(1.4.1)для плоскорадиальной фильтрации:
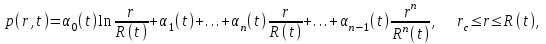 (1.4.2)
(1.4.2)где число членов n выбирается в зависимости от желаемой точности решения.
3. Коэффициенты многочлена а0, а1, а2, ..., аn, а также размер области возмущения l(t) (или R(t)) находятся из условий на галерее (или на забое скважины), из условий непрерывности давления и гладкости кривой давления на границе области возмущения, а также из особых интегральных соотношений. Число этих интегральных соотношений зависит от показателя степени n, а следовательно, от числа членов многочлена, входящего в уравнение. Показатель степени n в свою очередь выбирается в зависимости от желательной степени точности решения задачи. Чем больше число n, тем выше точность решаемой задачи. Интегральные соотношения находятся следующим образом.
В случае притока к галерее правая и левая части уравнения пьезопроводности (1.4.3) умножаются на хk (где k=0, 1, 2, ...) и интегрируются по всей возмущенной области:
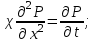 (1.4.3)
(1.4.3)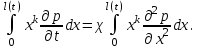 (1.4.4)
(1.4.4)Для случая притока к скважине берется дифференциальное уравнение (1.4.5), его правая и левая части умножаются на rk (где k = 1, 2, ...) и проводится интегрирование по всей возмущенной области:
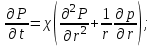 (1.4.5)
(1.4.5)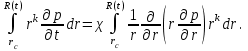 (1.4.6)
(1.4.6)Если в уравнения (1.4.4) и (1.4.6) подставить соответственно выражения (1.4.1) и (1.4.2) и проинтегрировать, то получатся недостающие соотношения для определения коэффициентов а0(t), а1(t),... и l(t) или R(t).
Первое из этих интегральных соотношений (при k =0, если рассматривается приток к галерее, и при k =1 для притока к скважине) представляет собой уравнение материального баланса и из него находится координата границы возмущенной области
l(t) или R(t).
Если принять в формуле (1.4.1) n =1, а в формуле (1.4.2) n =0, то получатся решения, соответствующие методу ПССС (1.2.3), (1.2.8), в зависимости от условий на галерее или на забое скважины; если же n = 2 в (1.4.1), то из метода интегральных соотношений вытекает, как частный случай, метод А. М. Пирвердяна [2].
ГЛАВА 2. РАСЧЕТНАЯ ЧАСТЬ
2.1 Исследование прямолинейно-параллельного установившегося фильтрационного потока однородной несжимаемой жидкости по закону Дарси в однородном пласте (приток к галерее)
Задача
Определить закон распределения давления, градиента давления и скорости фильтрации по длине пласта (в математическом и графическом виде), дебит галереи, закон движения частиц жидкости и средневзвешенное по объему порового пространства.
Таблица 2.1.1 – Исходные данные
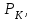 МПа МПа | 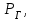 МПа МПа | 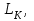 км км | 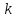 , мкм , мкм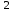 | 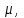 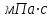 | 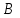 , м , м | 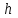 , м , м | 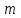 ,% ,% |
| 9,4 | 6,9 | 8,5 | 0,7 | 2,5 | 160 | 7 | 17 |
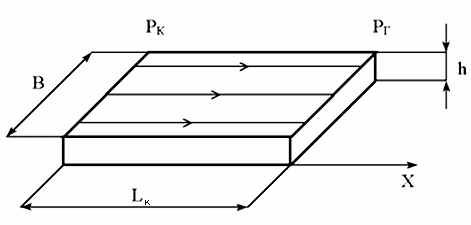
Рисунок 2.1.1 - Схема прямолинейно-параллельного фильтрационного потока в пласте
-
Закон распределения давления при установившейся фильтрации жидкости в полосообразном пласте:
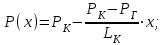
(2.1.1)
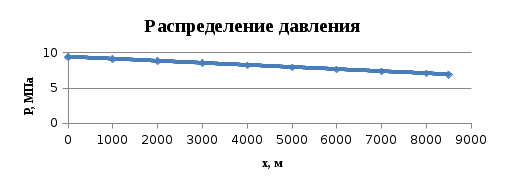
Рисунок 2.1.2 - График распределение давления по длине пласта
Таблица 2.1.2 – Распределение давления
| P(x), МПа | 9,4 | 9,106 | 8,812 | 8,518 | 8,224 | 7,929 | 7,635 | 7,341 | 7,047 | 6,9 |
| x, м | 0 | 1000 | 2000 | 3000 | 4000 | 5000 | 6000 | 7000 | 8000 | 8500 |
-
Закон распределения градиента давления:
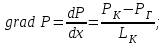 (2.1.2)
(2.1.2)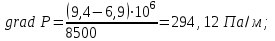
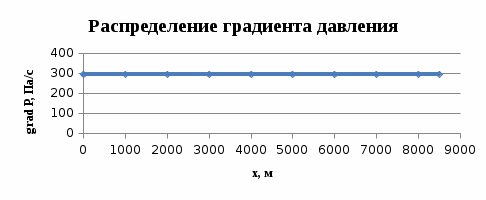
Рисунок 2.1.3 - График распределения градиента давления по длине пласта
-
Закон распределения скорости фильтрации:
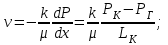 (2.1.3)
(2.1.3)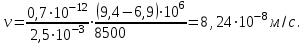
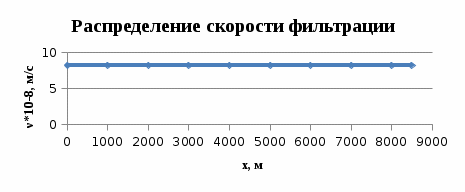
Рисунок 2.1.4 - График распределения скорости фильтрации по длине пласта
-
Дебит галереи:
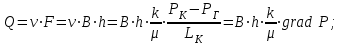 (2.1.4)
(2.1.4)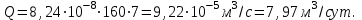
5. Закон движения частиц жидкости:
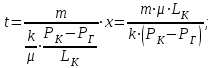 (2.1.5)
(2.1.5)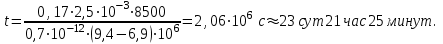
6. Средневзвешенное по объему порового пространства давление:
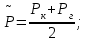 (2.1.6)
(2.1.6)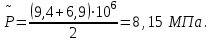
Вывод: при прямолинейно-параллельной фильтрации несжимаемой жидкости в однородном пласте давление падает согласно линейному закону, скорость фильтрации и градиент давления остаются неизменными на протяжении всего пласта согласно закону Дарси, средневзвешенное пластовое давление по объему пор равно среднему арифметическому давлению контура и галереи [3].
2.2 Исследование плоскорадиального установившегося фильтрационного потока несжимаемой жидкости по закону Дарси в однородном пласте (приток совершенных скважин)
Задача
Определить закон распределения давления, градиента давления и скорости фильтрации по длине пласта (в математическом и графическом виде), дебит скважины, закон движения частиц жидкости и средневзвешенное по объему порового пространства пластовое давление при следующих исходных данных:
Таблица 2.2.1 – Исходные данные
 МПа МПа | 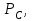 МПа МПа | 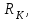 м м | 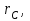 м м |  , мкм , мкм |   |  , м , м |  ,% ,% |
| 9,4 | 6,9 | 1600 | 0,16 | 0,7 | 2,5 | 7 | 17 |
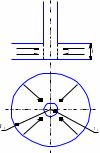
Рисунок 2.2.1 - Схема плоскорадиального потока
-
Определение закона распределения давления в пласте:
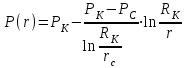 (2.2.1)
(2.2.1)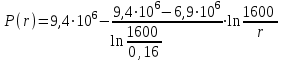 ;
;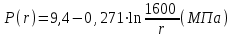 .
.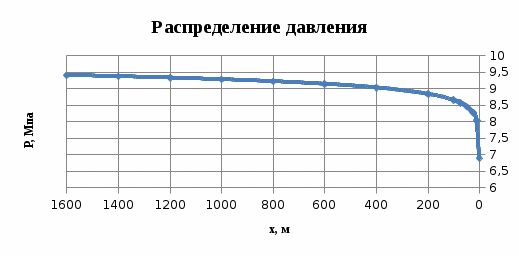
Рисунок 2.2.2 - График распределения давления в пласте
Таблица 2.2.2 – Распределение давления
| r, м | P(r), МПа |
| 10 | 8,022 |
| 25 | 8,271 |
| 50 | 8,459 |
| 75 | 8,569 |
| 100 | 8,647 |
| 300 | 8,946 |
| 500 | 9,084 |
| 700 | 9,176 |
| 900 | 9,244 |
| 1100 | 9,298 |
| 1300 | 9,344 |
| 1500 | 9,382 |
| 1600 | 9,400 |
| 1500 | 9,382 |
| 1600 | 9,400 |
