Файл: Приближенные методы решения задач теории упругого режима фильтрации.docx
Добавлен: 17.10.2024
Просмотров: 26
Скачиваний: 0
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
-
Определение градиента давления:
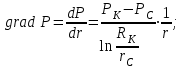 (2.2.2)
(2.2.2) 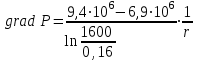 .
.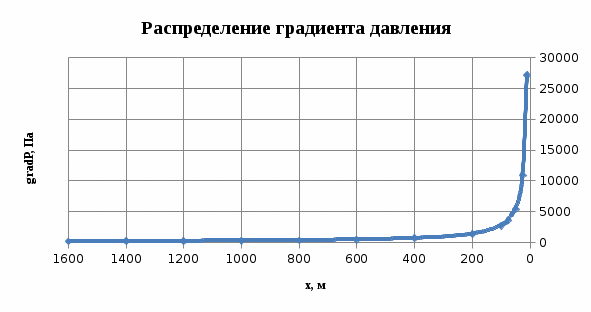
Рисунок 2.2.3. - График распределения градиента давления
Таблица 2.2.3 – Распределение градиента давления
| r, м | grad P, Па |
| 10 | 27143,405 |
| 25 | 10857,362 |
| 50 | 5428,681 |
| 75 | 3619,121 |
| 100 | 2714,341 |
| 300 | 904,780 |
| 500 | 542,868 |
| 700 | 387,763 |
| 900 | 301,593 |
| 1100 | 246,758 |
| 1300 | 208,795 |
| 1500 | 180,956 |
| 1600 | 169,646 |
| 1500 | 180,956 |
| 1600 | 169,646 |
-
Определение скорости фильтрации:
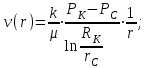 (2.2.3)
(2.2.3) 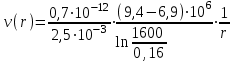 ;
;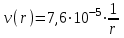 .
.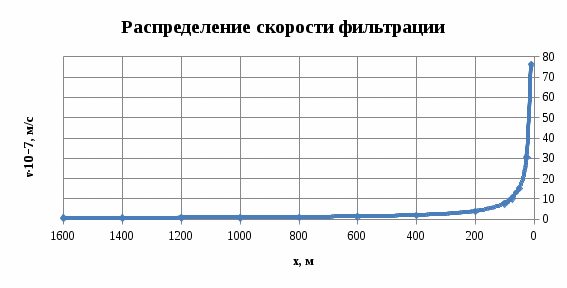
Рисунок 2.2.4. - График распределения скорости фильтрации в пласте
Таблица 2.2.4 – Изменение скорости фильтрации в пласте
| r, м | ν∙10-8,м/c |
| 10 | 760,015 |
| 25 | 304,006 |
| 50 | 152,003 |
| 75 | 101,335 |
| 100 | 76,002 |
| 300 | 25,334 |
| 500 | 15,200 |
| 700 | 10,857 |
| 900 | 8,445 |
| 1100 | 6,909 |
| 1300 | 5,846 |
| 1500 | 5,067 |
| 1600 | 4,750 |
| 1500 | 5,067 |
| 1600 | 4,750 |
-
Определение дебита скважины:
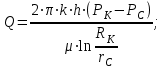 (2.2.4)
(2.2.4)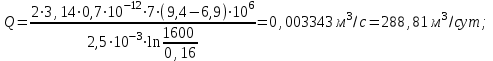
-
Определение закона движения частиц жидкости:
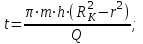 (2.2.5)
(2.2.5)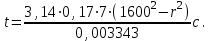
Тогда время движения частицы жидкости от контура питания до забоя:
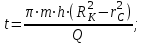 (2.2.6)
(2.2.6)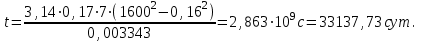
-
Средневзвешенное по объему порового пространства давление:
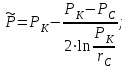 (2.2.7)
(2.2.7)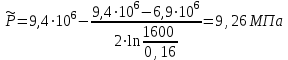
Вывод: при плоскорадиальной установившейся фильтрации однородной несжимаемой жидкости в однородном пласте скорость и градиент давления резко изменяется в призабойной зоне скважины (депрессионная воронка). Средневзвешенное пластовое давление по объему близко к значению давления на контуре питания. Это объясняется что, давление резко меняется только в призабойной зоне скважины, а затем давление распределяется плавно[3].
2.3 Исследование прямолинейно-параллельного установившегося фильтрационного потока однородной несжимаемой жидкости в неоднородных пластах
Задача
Определить закон распределения давления, градиента давления и скорости фильтрации по длине пласта (в математическом и графическом виде), дебит галереи и средний коэффициент проницаемости для двух случаев неоднородности пласта: слоисто-неоднородного и зонально-неоднородного - при следующих исходных данных:
Таблица 2.3.1 - Исходные данные
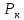 , ,МПа | 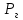 , ,МПа | 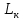 , ,км | В, м | h, м | 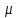 , ,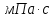 | 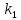 , ,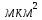 | 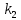 , ,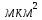 | Слоисто- | Зонально- | ||
| Неоднородный | |||||||||||
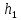 , ,м | 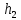 , ,м | 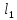 , ,км | 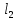 , ,км | ||||||||
| 9,4 | 6,9 | 8,5 | 160 | 8 | 2,5 | 0,7 | 0,2 | 4 | 4 | 4,5 | 4 |
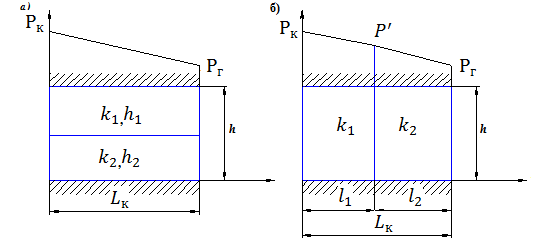
Рисунок 2.3.1 - Схема прямолинейно–параллельного фильтрационного потока в слоисто-неоднородном (а) и зонально-неоднородном (б) пластах
Рассмотрим слоисто-неоднородный пласт:
-
Определение закона распределения давления в пласте:
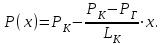 (2.3.1)
(2.3.1)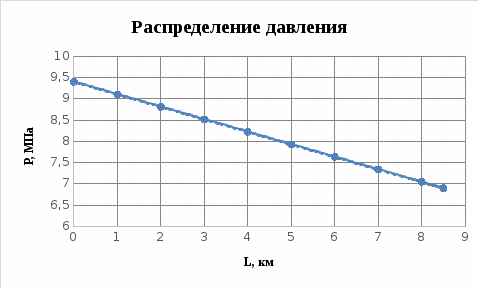
Рисунок 2.3.2 - График распределения давления в пласте
-
Определение градиента давления:
 (2.3.2)
(2.3.2)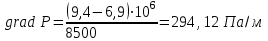
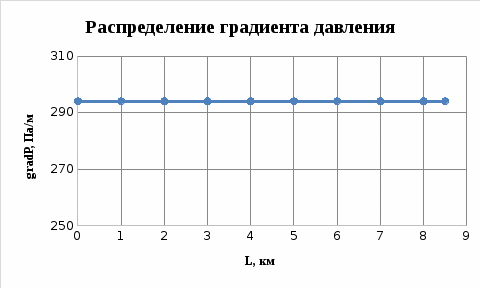
Рисунок 2.3.3 - График распределения градиента давления в пласте
-
Определение скорости фильтрации:
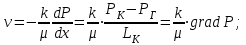 (2.3.3)
(2.3.3)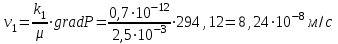 ;
;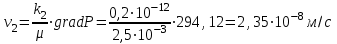 .
.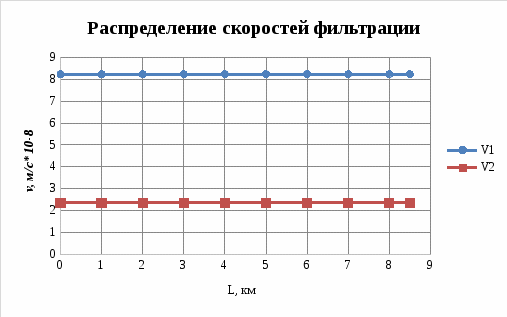
Рисунок 2.3.4. - График распределения скоростей фильтрации в пласте
-
Определение дебита галереи:
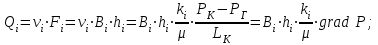 (2.3.4)
(2.3.4)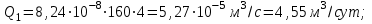
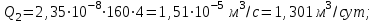
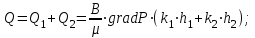 (2.3.5)
(2.3.5)
-
Определение средней проницаемости пласта:
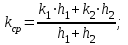 (2.3.6)
(2.3.6)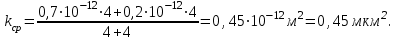
Рассмотрим зонально-неоднородный пласт:
Для начала определим давление на границе между зонами, основываясь на уравнении неразрывности
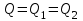 .
.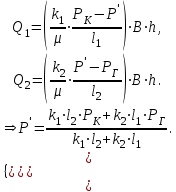
(2.3.7)
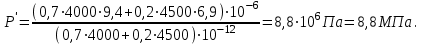
-
Закон распределения давления:
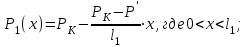 (2.3.8)
(2.3.8)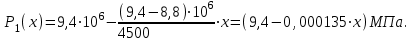
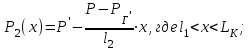 (2.3.9)
(2.3.9)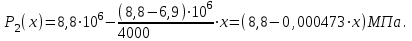
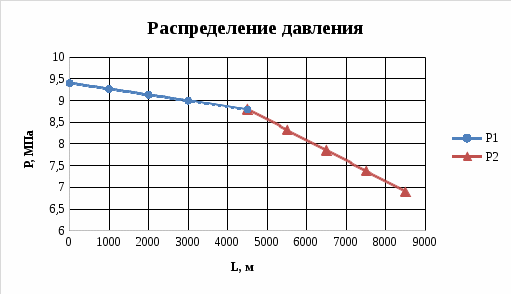
Рисунок 2.3.5 - График распределения давления в пласте при зонально-неоднородном пласте
2. Определение градиента давления:
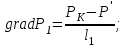 (2.3.10)
(2.3.10)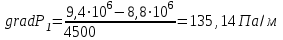 .
.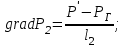 (2.3.11)
(2.3.11)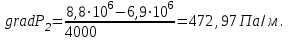
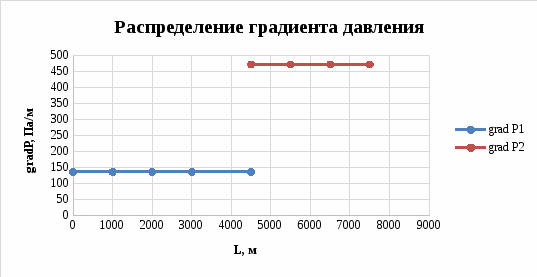
Рисунок 2.3.6 - График распределения градиента давления в пласте
3. Определим скорость фильтрации:
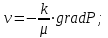 (2.3.12)
(2.3.12)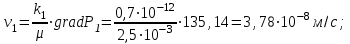
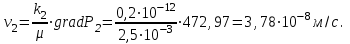
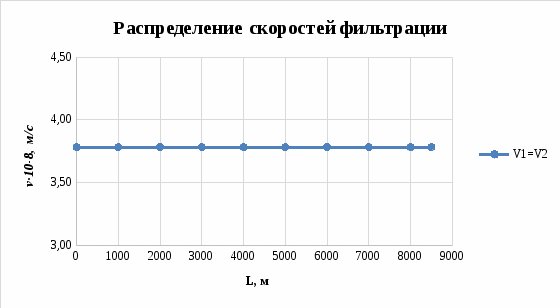
Рисунок 2.3.7 - График распределения скоростей фильтрации в пласте
4. Определение дебита галереи:
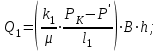 (2.3.13)
(2.3.13)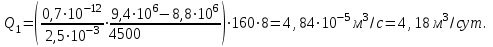
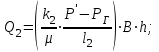 (2.3.14)
(2.3.14)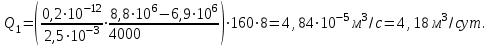
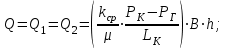 (2.3.15)
(2.3.15)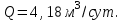
5. Определение средней проницаемости пласта:
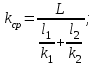 (2.3.16)
(2.3.16)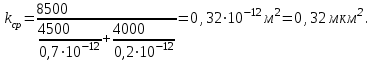
Вывод: при плоскопараллельной установившейся фильтрации несжимаемая жидкость в слоисто–неоднородном пласте движется под действием постоянного градиента давления с разной скоростью в каждом из пропластков и обладает большей средней проницаемостью, чем в зонально–неоднородном пласте, где фильтрация жидкости происходит с одинаковой скоростью, но с разным градиентом давления [7].
ЗАКЛЮЧЕНИЕ
В данной курсовой работе были рассмотрены приближенные методы решения задач теории упругого режима фильтрации, удалось углубить и закрепить теоретические знания, полученные во время лекционных, лабораторных и практических занятий, а также приобрести новые посредством изучения методической, учебной и специальной литературы по данной теме.
В теоретической части были рассмотрены: метод последовательной смены стационарных состояний, метод А.М. Привердяна и метод интегральных соотношений.
Практическая часть данной курсовой работы основана на математическом моделировании процессов фильтрации пластовых флюидов. В ней были исследованы прямолинейно-параллельный и плоскорадиальный установившиеся фильтрационные потоки однородной несжимаемой жидкости по закону Дарси в однородном пласте, а также прямолинейно-параллельная и плоскорадиальная установившиеся фильтрации однородной несжимаемой жидкости в слоисто- и зонально-неоднородных пластах.
Применение математического моделирования позволяет решать гидродинамические задачи, связанные с разработкой, с максимальным приближением к реальным условиям при учете всех факторов, влияющих на движение углеводородной жидкости в пласте по направлению к забою скважины.
СПИСОК ЛИТЕРАТУРЫ
-
Басниев К.С. Подземная гидромеханика / К.С. Басниев, И.Н. Кочина, В.М. Максимов – Москва: Недра, 1993.– 376 с. -
Басниев К.С. [и др.] / Подземная гидромеханика; Российский государственный университет нефти и газа имени И.М. Губкина.– 2-е изд., испр.– М.; Ижевск: Ин-т компьютер. исслед., 2006 .– 495 с. -
Евдокимова Е. А. Сборник задач по подземной гидромеханике / Е. А. Евдокимова, И. Н Кочина.: Недра, 1979. – 168 с. -
Квеско Б.Б. Подземная гидромеханика/ Квеско Б.Б., Карпова Е.Г. – Томск: Томский политехнический университет, 2010.– 174 с. -
Пономарева, И.Н. Подземная гидромеханика: Учебное пособие / И.Н. Пономарева, В.А. Мордвинов. – Пермь: Перм. гос. техн. ун-т, 2009. – 103с. -
Пыхачев Г.Б., Исаев Р.Г. «Подземная гидравлика», М.Недра, 1973. -
Рогачев М.К. Подземная гидромеханика: Лабораторный практикум / М.К. Рогачев, А. Ю. Харин. – СПб.: СПГГИ(ТУ), 2006. – 83 с. -
Щелкачев В. Н. Подземная гидравлика: Учебное пособие для вузов / В.Н.Щелкачев, Б.Б. Лапук.– М.; Ижевск : РХД, 2001.– 735 с.
